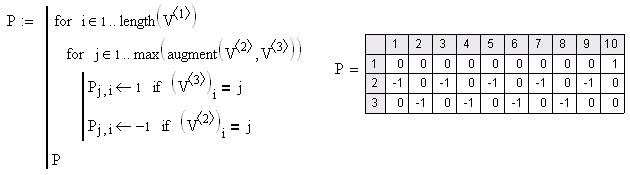Kolomoets Valentina 

Faculty: Electrotechnical (ETF)

Speciality "Electrical Power Statiots"(EPS)

"Discrete mathematical model for analysis of transients in synchronous generators and block transformers of Electric Power Stations"

Scientific adviser: Dr.Sc., Prof. Vitaliy Sivokobylenko 

1. Introduction
2. A theme urgency
3. Communication with the science programs, plans, themes
4. Goal of work
5. Scientific novelty of the receivid results
6. Practical value
7. Approbation the work results
8. Overview of research and dvelopment on the subject
9. The main content of the work
10. Conclusions
11. Bibliography

Due to the rapid development of computer technology have become increasingly interested in mathematical models of power supply systems. Is urgent to create universal models to investigate both short and long transients in a group of machines based on their mutual influence [3]. If there is information on system parameters and topological relationships between its elements can be constructed a mathematical model of the object with which the analysis of its behavior in various modes.

Widely used in industry received frequency converters. They are designed for a smooth change of speed and torque of the motor shaft.

Currently, due to the wide application of mathematical modeling is a set of programs for calculation of electric modes, short-circuit currents, electric and magnetic fields

For the development of multi-machine power systems are actual development and creation of mathematical models of these systems. They must differ a high degree of Conformity of real objects and allows to investigate the features of transitional and emergency modes, to reduce design time and costs for field experiments [3].

There are two main approaches in the development of mathematical models of this class: using explicit or implicit numerical integration methods [5]. The use of implicit methods for the numerical integration of differential equations is more promising, because with their help it is possible to obtain a stable solution in the simulation of multiple switching in networks of any complexity [5].

Qualifying work of the master performed throughout 2010 – 2011. According to the scientific direction of the Department of “Electric Power Plants” of the Donetsk National Technical University.

The aim is the development and creation of a discrete mathematical model of the main circuit wiring power station based on the total differential equations.

Research objectives:

• creation of a discrete mathematical model and the choice of parameters of the basic elements of ES;
• creation of complex algorithms and programs for the formation of different types of mathematical models;
• development of mathematical models of multicomputer systems based on discrete
• analyze the behavior of the main elements of the circuit of electrical connections power at occurrence and off balanced and unbalanced short circuit of varying duration.

1. Discrete mathematical models of synchronous machines, allowing to solve the problem of numerical instability in simulation modes of power station;
2. Synthesis parameters of the discrete equivalent circuits of electric machines based on catalog data;
3. The simulation method regimes of commutations switch;
4. A mathematical model of the inverter.

Developed a discrete mathematical model can be used for modeling and analysis of a short circuit, the choice of switching equipment and relay protection and automatics.

The practical value of frequency start is as follows:

• increases the reliability of own needs of ES;
• prolongs the life of AM;
• increase the intervals between repairs;
• reduced maintenance costs.

Publication in the proceedings IX International scientific conference of young scientists and specialists "Electromechanical and power systems, modeling and optimization" on the theme: "Mathematical Modeling of frequency starting of induction motors.

18 – 20th April 2011 attended a conference dedicated to the 60 th anniversary of Sevastopol National Technical University. The report was on the theme "Mathematical Modeling of frequency starting of induction motors in the system of auxiliary power stations."

1. Global. Currently, many firms are engaged in development of mathematical modeling of transitional processes, improving existing programs and packages for the creation of mathematical models.
2. National. Mathematical model plays an important role not only in power stations, but in any enterprise. If the machine will operate continuously, it will raise the potential of the Donets Basin, and later Ukraine.
3. Local. Most master's and postgraduate work of the Department of ES associated with mathematical modeling. This explains the relevance of the mathematical models and the universality of their application.

Qualifying work is performed in accordance with this plan:

Formation of the full nonlinear differential equations of all elements of the circuit of electrical connections.

In the models of rotating electrical machines are used an equivalent circuit with multicircuit rotor.

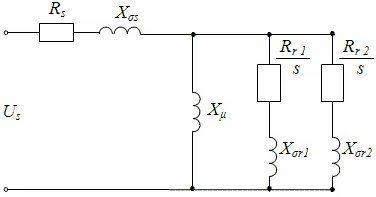
Figure 1 – Equivalent circuit of induction motor with double-circuit rotor.

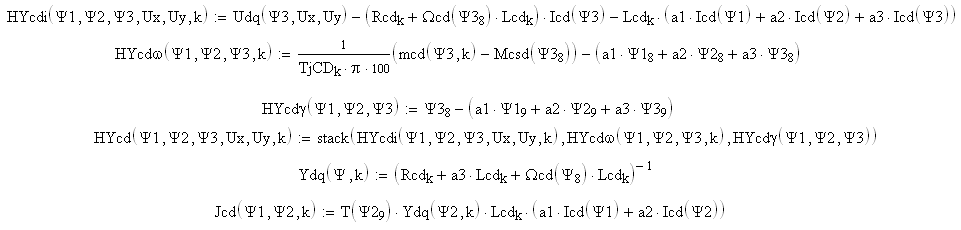
Figure 2 – The system of nonlinear algebraic equations for SM

Figure 3 – The system of nonlinear algebraic equations for AM

Transformation of nonlinear equations in finite-difference equations

Consideration of methods of solving equations

– method of simple iterations

– Newton's method

– Euler's method

– Runge-Kutta method, etc.

Accounting for the relationship of elements of main circuit wiring

Compilation of topological matrices given schema

Figure 4 – The matrix of nodal conductances

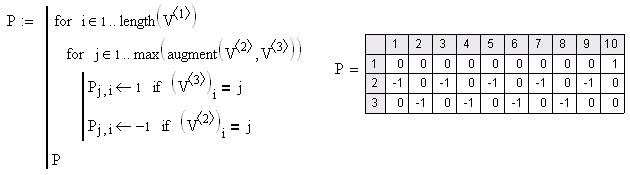
Figure 5 – Matrix compounds

Development of a technique of forming a mathematical model of electrical connections of ES given structure

Creating a mathematical model of own needs of ES with frequency regulation

In this paper, we consider the possibility of using для переменного режима пуска AM only one inverter

(animation consists of 6 shots with a delay of 50 ms between frames, the number of cycles of reproduction is limited to 5 th)

Figure 6 – Examples of tasks laws frequency voltage in accordance with the laws

Analysis of the transients and the main electric circuit of ES

1. Been developed discrete equivalent circuit of the main elements of power electric circuits. They are based on implicit methods for the numerical integration of differential equations and are designed for analysis of transient and emergency regimes
2. Been developed the method of accounting of magnetic saturation of the transformer in the analysis of transients in transformers.
3. Been developed the mathematical model of the frequency converter in which output voltage, frequency, output voltage and its amplitude is changed by a specified law.
4. With using the developed methods will be calculated the transition process in the system auxiliary power station, which caused a short circuit and subsequent action of relay protection and automation.
5. An immediate task is to improve the program for the possibility of calculating the system using discrete methods.

1. Коломоец В.В, Сивокобыленко В.Ф. Математическое моделирование частотного пуска асинхронных двигателей // Сборник статей IX международной научно-технической конференции молодых ученых и специалистов "Электромеханические и энергетические системы,методы моделирования и оптимизации" [электронный ресурс] – Режим доступа: ESMO.KDU.EDU.UA/STATTI/269.PDF.
2. Коломоец В.В, Сивокобыленко В.Ф. Математическое моделирование частотного пуска асинхронных двигателей в системе собственных нужд электрических станций // Електротехнічні та електромеханічні системи: Матеріали XVI Всеукраїнської студентської науково–технічної конференції, м. Севастополь, 18 – 20 квітня 2011 / Міністерствово освіти і науки, молоді та спорту України, Севастопопольський національний технічний університет; наук. ред. О.М. Дегтярьов – Севастополь: СевНТУ, 2011. – 62 – 63 с.
3. Сивокобыленко В.Ф., Лебедев В.К. Переходные процессы в системах электроснабжения собственных нужд электростанций: Учеб. Пособие. – Донецк: ДонНТУ, 2002. – 136 с.
4. Устенко А.С. Основы матеметического моделирования и алгоритмизации процессов функционирования сложных систем – М.: Издательство “МИР”, – 2000. [электронный ресурс] – Режим доступа: http://ustenko.fromru.com/part1.html
5. Сивокобыленко В.Ф. Переходные процессы в многомашинных системах электроснабжения электрических станций: Уч. пособие/ – Донецк, ДПИ, 1984. – 116 с.
6. Электрическая часть электростанций и подстанций: Справочные материалы для курсового и дипломного проектирования. Учеб. пособие для электротехнических специальностей вузов/ Крючков И. П., Кувшинский Н. Н., Неклепаев Б. Н.; Под ред. Б. Н. Неклепаева – 3–е изд., перераб. и доп. – М.: Энергия, 1978 – 456 с.
7. Сивокобыленко В. Ф., Костенко В. И. Математическое моделирование электродвигателей собственных нужд электрических станций. Учебное пособие. – Донецк: ДПИ, 1979. – 110с.
8. Ойрех Я. А., Сивокобыленко В. Ф. Режимы самозапуска асинхронных двигателей. – М.: Энергия, 1974. – 96с.
9. Сивокобыленко В. Ф., Павлюков В. А. Расчет параметров схем замещения и пусковых характеристик глубокопазных асинхронных машин. – Электричество, 1979, №10.
10. Сивокобыленко В. Ф., Лебедев В. К. Определение параметров схем замещения для анализа режимов работы синхронных двигателей. – Электротехника, 1982, №12.
11. Сыромятников И. А. Режимы работы синхронных и асинхронных двигателей/ Под ред. Л. Г. Мамиконянца. – 4-е изд., перераб. и доп. – М.: Энергия, 1974. – 96с.
12. Перхач В.С. Математичні задачі електроенергетики. "Вища школа", Л. – 1989, 464
13. Демирчян К. С., Бутырин П. А. О Моделирование и машинный расчет электрических цепей: Учеб. пособие для электр. и электроэнерг. спец. вузов. – М.: Высш. шк., 1988. – 335 с.

!!! When writing this abstract the master’s qualification work is notcompleted. Date of final completion of work: December, 2010. Full text of the work and materials on a work theme can be received from the author or his scientific supervisor after that date.