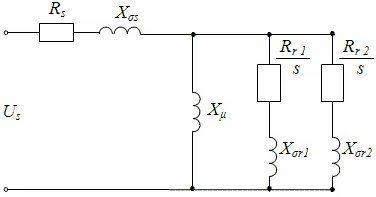
Рисунок 1 – Схема заміщення глубокопазного асинхронного двигуна з двоконтурним ротором.

У зв'язку з бурхливим розвитком обчислювальної техніки, а також з підвищенням вимог до точності моделювання при розробці та створенні високонадійних систем електропостачання АЕС, ТЕС і інших відповідальних установок з великими АД і СД, значно зросла зацікавленість до математичних моделей у системах електропостачання, які грунтуються на повних рівняннях Парка-Горєва як для машин, так і для всіх елементів живлючої мережі. Актуальним є створення універсальних моделей, що дозволяють дослідити як короткочасні (АПВ, АВР, короткі замикання), так і тривалі (пуск, самозапуск) перехідні процеси в групі машин з урахуванням їх взаємного впливу, з урахуванням залежностей параметрів від витіснення струмів і насичення магнітних кіл [3]. При наявності інформації про параметри системи та топологічних зв'язках між її елементами може бути побудована математична модель об'єкта, за допомогою якої виконується аналіз її поведінки в різних режимах роботи.
Широке застосування в промисловості отримали частотні перетворювачі. Частотно–регульований електропривод призначений для плавної зміни швидкості і моменту обертання валу електродвигуна шляхом зміни частоти живлячої напруги. При цьому:
В даний час у зв'язку з широким застосуванням математичного моделювання існує безліч відповідних програм розрахунку електричних режимів, струмів короткого замикання, електричних і магнітних полів.
Для подальшого вдосконалення та розвитку багатомашинних систем електропостачання актуальними є розробка та створення математичних моделей зазначених систем, що відрізняються високим ступенем адекватності реальним об'єктам та дозволяють дослідити особливості перехідних і аварійних режимів, скоротити терміни проектування і витрати на натурні експерименти [3].
Існує багато способів складання і рішення систем диференціальних рівнянь електричних станцій, чимало з них складено з деякими припущеннями, наприклад:
Залежно від складності електричної системи, досліджуваного режиму та низки інших факторів застосовуються два основних підходи при розробці математичних моделей такого класу: із застосуванням явних або неявних методів чисельного інтегрування [5]. Аж до теперішнього часу, в раніше розроблених методах має місце дилема між отриманням необхідної точності розрахунку і збереженням при цьому чисельної стійкості і швидкодії. Тому питання пошуку більш досконалих алгоритмів розрахунку перехідних режимів залишається відкритим, що особливо актуально для мікропроцесорних терміналів, що працюють в режимі РЧ.
Застосування неявних методів чисельного інтегрування диференціальних рівнянь (ДУ) є більш перспективним, оскільки з їх допомогою можливо отримати стійке рішення при моделюванні багаторазових комутацій в електричних мережах будь-якої складності [5].
Кваліфікаційна робота магістра виконувалася впродовж 2010 – 2011 рр. згідно з науковими напрямками кафедри «Електричні станції» Донецького національного технічного університету.
Метою роботи є розробка і створення дискретної математичної моделі головної схеми електричних з'єднань електричної станції на основі повних диференціальних рівнянь. Для створення універсальної математичної моделі потрібні повні математичні описи всіх елементів головної схеми: генераторів, трансформаторів, синхронних і асинхронних двигунів та ін.
Задачі дослідження, поставлені в даній роботі:
Методи дослідження. Теоретичні дослідження базуються на основних положеннях теорії електротехніки і режимів роботи електростанцій і систем, теорії стаціонарних і перехідних процесів машин змінного струму, чисельних методах аналізу і обчислювальної техніки в системах електропостачання.
Предметом дослідження є перехідні процеси в схемі електричних з'єднань електростанції.
Об'єктом дослідження є дискретні математичні моделі елементів головної схеми електричних з'єднань електричної станції.
Розроблена дискретна математична модель може знайти широке практичне застосування для моделювання та аналізу різного роду коротких замикань (симетричних і несиметричних), вибору комутаційної апаратури та пристроїв релейного захисту та автоматики. Модель може використовуватися не тільки на електричних станціях, але й на будь-якому підприємстві, яке використовує велику кількість асинхронних двигунів, безперебійна робота яких повинна забезпечувати безаварійне виробництво, що особливо важливо для великих підприємств Донбасу. Частотно-регульований електропривод призначений для плавної зміни швидкості і моменту обертання валу електродвигуна шляхом зміни частоти живлячої напруги.
Практична цінність частотного пуску полягає в наступному:
Публікація в збірнику матеріалів IX Міжнародній науково-технічній конференції молодих вчених та спеціалістів "Електромеханічні та енергетичні системи, методи моделювання та оптимізації » на тему: "Математичне моделювання частотного пуску асинхронних двигунів ".
18 – 20 квітня 2011 брала участь на конференції присвяченій 60–річчю Севастопольського національного технічного університету "Електротехнічні та електромеханічні системи". Доповідь була на тему "Математичне моделювання частотного пуску асинхронних двигунів в системі власних потреб електричних станцій". "В даний час у зв'язку з широким застосуванням частотних перетворювачів (ЧП) у промисловості, стає актуальним питання дослідження частотного пуску і перехідних процесів (ПП) в асинхронних двигунах (АД) в різних режимах. У зв'язку з високою вартістю частотних перетворювачів (ЧП) в даній роботі розглянуто можливість використання для режимів почергового пуску АД тільки одного НП" [2].
Для аналізу режимів роботи енергосистем широко застосовують методи математичного моделювання. Це пов'язано з бурхливим розвитком обчислювальної техніки, а також з підвищенням вимог до точності моделювання при розробці та створенні високонадійних систем електропостачання АЕС, ТЕС.
Наведемо огляд досліджень і розробок по темі:
Кваліфікаційна робота виконується у відповідності з таким планом:
Рівняння для елементів, які мають пофазну симетрією (ЛЕП, трансформатор, кабель), будуть записуватися в двофазної системі х, y, тобто в нерухомій щодо статорів генераторів. Для симетричних електричних машин (АД) використовуються осі х, y, а для несиметричних (синхронні генератори та двигуни) – система координат, жорстко пов'язана з осями d, q ротора. При цьому на кожному кроці розрахунку для синхронних машин здійснюється перерахунок режимних параметрів від осей d, q до осей всіх інших елементів х, y.
У моделях електричних машин, що обертаються (двигуни і генератори), використовуються схеми заміщення з багатоконтурний ротором, що дозволяє більш точно враховувати ефект витіснення струму в роторі.

Рисунок 1 – Схема заміщення глубокопазного асинхронного двигуна з двоконтурним ротором.
Для синхронних машин у зв'язку з наявністю на роторі обмотки збудження по поздовжній осі d ДУ доцільно вирішувати в осях d і q, жорстко пов'язаних з його ротором. Тільки в цих координатах в рівняннях вдається уникнути періодичних коефіцієнтів, що залежать від кутового повороту ротора.
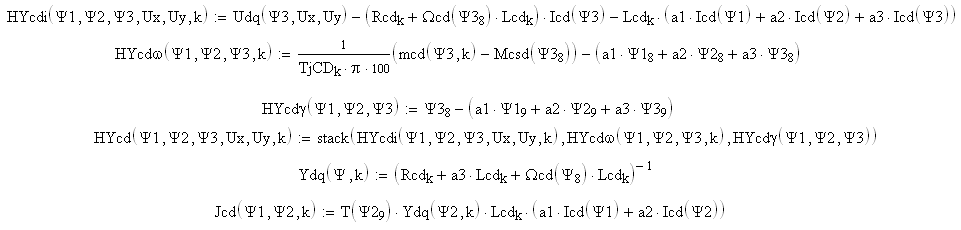
Рисунок 2 – Система нелінійних алгебраїчних рівнянь для СД

Рисунок 3 – Система нелінійних алгебраїчних рівнянь для АД
Метод кінцевих різниць – широко відомий і найпростіший метод інтерполяції. Його суть полягає в заміні диференціальних коефіцієнтів рівняння на різницеві коефіцієнти, що дозволяє звести рішення диференціального рівняння до вирішення його різницевого аналога, тобто побудувати його кінцево–різницеву схему.
– метод простих ітерацій
– метод Ньютона
– метод Ейлера
– метод Рунге-Кутта та ін.
Розробляється математична модель багатомашинної системи на основі дискретних математичних моделей і з урахуванням взаємного зв'язку всіх елементів схеми електричних з'єднань.
Формується матриця вузлових провідностей V, матриця з'єднань Р і т.д

Рисунок 4 – Матриця вузлових провідностей
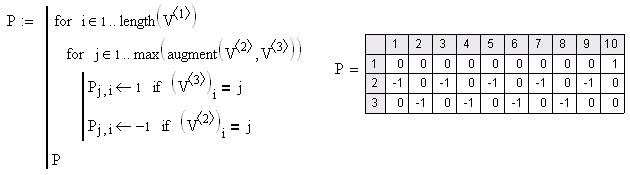
Рисунок 5 – Матриця з'єднань
У зв'язку з високою вартістю частотних перетворювачів (ЧП) в даній роботі розглянуто можливість використання для режимів почергового пуску АД тільки одного ЧП.

Рисунок 6 – Схема СВП блоку 200 МВт
Вихідна напруга ЧП підключена до обхідної системи шин (ОСШ).
Через індивідуальний вакуумний контактор напругу з ОСШ може бути подано на будь-який АД.
Модель ЧП повинна відповідати таким вимогам:

(анімація складається з 6 кадрів з затримкою 50 мс між кадрами; кількість циклів відтворення обмежено 5-ма)
Рисунок 7 – Приклади задання законів зміни частоти напруги у відповідності з законами:

!!! При написанні даного автореферату магістерська робота ще не завершена. Дата остаточного завершення роботи: грудень 2011 Повний текст роботи та матеріали по темі можуть бути отримані у автора або його наукового керівника після зазначеної дати.
На початок