Введення
Забезпечення електромагнітної сумісності ( ЕМС ) є одним з основних вимог до систем електропостачання. Завищення оцінок ЕМС призводить до необгрунтованого збільшення капіталовкладень, а заниження — до збитку від додаткових втрат електроенергії, зниження терміну служби електрообладнання, погіршення якості продукції. У зв'язку з цим високі вимоги пред'являються до обгрунтованості і точності методів оцінювання ЕМС як на стадії проектування, так і в експлуатації систем електропостачання.
ЕМС — впливає на електроприймачі. Це обумовлює практичну актуальність роботи.
Для оцінки ЕМС необхідно мати графіки зміни ( навіть для оцінки коливань).
Практика застосування ГОСТ 13109–97 на норми якості електроенергії в системах електропостачання виявила основний науковий протиріччя: існуючі показники якості напруги (ПКН) орієнтовані на незмінні у часі електричні періодично змінюються порушення (перешкоди) ЕМС, в той час як в діючих електричних мережах перешкоди мають випадковий характер. Тому стає незрозуміло, з якою ординатою перешкоди порівнювати нормативне значення показника якості напруги і як використовувати ті характеристики періодичної перешкоди, які втрачають сенс для неперіодичної перешкоди. Цим пояснюється необхідність застосування імовірнісних методів для аналізу процесів у системах електропостачання. Статичне моделювання (імітація) процесів х(t) у системах електропостачання дозволяє вирішувати нелінійні задачі, які не мають аналітичного рішення. У нашому випадку для визначення параметрів ЕМС необхідно з високою точністю імітувати характеристики вхідний перешкоди, в якій заздалегідь є відомими нормальна функція розподілу і показова кореляційна функція.
Актуальність
У практиці відомі лише граф однохвилинних відхилень напруги у зв'язку з цим науковий інтерес представляють розробки методу синтезу графіків напруги по однохвилинний відхилень напруги.
Вперше запропоновано метод синтезу діючих значень за однохвилинним значенням напруги, новизна якої полягає в еквівалентній заміні однохвилинного осереднення на еквівалентну інерційне згладжування.
Вихідні — однохвилинний графік.
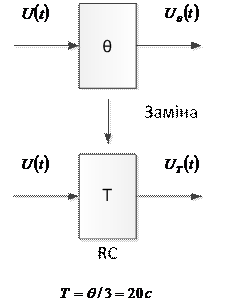
Синтез відновлення. Ідея полягає в тому, що замість однохвилинного осереднення ставиться у відповідному еквіваленті інерційне згладжування з постійною часу 20 сек.
У моделях ЕМС зважувальні фільтри звичайно є лінійними системами. Процеси в фільтрах описуються лінійними диференціальними рівняннями, порядок n яких може бути великим. Знаходження аналітичного рішення таких рівнянь утруднено як при детермінованих, так і при випадкових перешкодах.
У таких випадках навіть при n = 2 доцільно використовувати метод парціальних реакцій, суть якого полягає в тому, що фільтр замінюється еквівалентною системою, яка складається з n паралельно включених інерційних ланок першого порядку. Парциальная реакція кожної ланки визначається дуже просто, а рішення зводиться до підсумовування парціальних реакцій.
Мета роботи
Є 
— одномінутне відхилення напруги. Треба знайти U(t) без осереднення по всіх фазах, тобто використовувати синтез (відновлення).
Відповідно до еквівалентного інерційного згладжування з постійного часу 20 сек.
У нас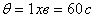 
Дає можливість відновити графік U(t), вважаючи що 
Відомо для RC
звідки маємо
Звідси випливає, що треба взяти вихідний графік 
і до нього додати графік його похідної, помноженої на T = 20 c.
Так як відхилення напруги невелике, то середньо–квадратичне осереднення можна замінити просто осреднением.
Зміст роботи
У моделі ЕМС лінійними є ВФ і інерційне або кумулятивне ланки. Початкові умови будемо вважати нульовими, що відповідає включенню об'єкта на стаціонарну перешкоду. Після включення на виході лінійної системи протікає нестаціонарний перехідний процес, а потім настає стаціонарний режим ( теоретично за 
), для якого визначаються показники ЕМС.
Детермінований вхідний процес може бути заданий по–різному. За заданою реалізації x(t) реакція Y(t) знаходиться або шляхом вирішення диференційного рівняння, що зв'язує вихідний і вхідний процеси в ВФ, або з використанням інтеграла Дюамеля:
де h(t) та g(t) – перехідна вагова функція ВФ,
— допоміжна змінна інтегрування.
Реалізація реакції починається з нульового значення.
Цей метод " послідовних інтервалів " дуже зручний при завданні процесу у вигляді гратчастої функції: дискретної послідовності ординат. Величина кроку дискретизації настільки мала, що в межах між суміжними ординатами процес можна вважати незмінним. У результаті виходить ступінчаста функція з однаковою тривалістю кожного ступеня. Для незмінною функції рішення диференціального рівняння отримати простіше.
Для періодичних перешкод можна не розраховувати перехідний процес, а відразу отримати реакцію в стаціонарному стані.
По–перше, це можна зробити шляхом розкладання вхідного процесу в ряд Фур'є. У цьому випадку амплітуда гармоніки множиться на значення АЧФ 
фільтра при частоті гармоніки, а до фази гармоніки додається значення фазочастотного функції ВФ при тій же частоті. Сума всіх отриманих гармонік дає періодичну реалізацію з тією ж тривалістю циклу, що й у вхідного процесу.
Гармоніки функціонально пов'язані між собою, але не корельованості. Оскільки їх середнє значення дорівнює нулю, то незалежно від фаз гармонік квадрати ефективних значень 
гармонік підсумовуються:
Якщо для вирішення завдання досить знати ефективне значення реакції, то будь–яка гармоніка або їх комбінація можуть розглядатися окремо, що є перевагою гармонійного аналізу.
Разом з тим, при застосуванні рядів Фур'є виникають труднощі з вибором кількості врахованих гармонік, особливо якщо під ВФ є диференцируюча ланка. Крім того, ряд точно не відтворює використовуються в проектуванні кусково–лінійні і ступінчасті функції в точках їх розриву — навіть при нескінченній кількості гармонік.
По–друге, реакція може бути отримана з використанням спільного рішення диференціального рівняння n–го порядку. У цьому випадку в загальному вигляді записуються вирази для кінцевих ординат кожної ділянки, які доповнюються умовами рівності ординат і n–1 похідних на межах ділянок, а також на початку і наприкінці циклу.
Висновок
Після закінчення дослідження ми отримаємо дані, зведені до Односекундний зняття показань, що призведе до більш точному увазі графіка залежності напруги від часу, і для оцінки її подальшого відхилення напруги.
Література
- ГОСТ 13109–97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине с 01.01.2000.
- Кузнецов В. Г., Куренный Э. Г., Лютый А. П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения. – Донецк: Норд–Пресс, 2005. –250с Свешников А. А.
- Бусленко Н.П. Моделирование сложных систем. – М.: Наука, 1978. – 400 с.
- Шидловский А.К., Кузнецов В.Г. Повышение качества энергии в электрических сетях. – Киев: Наукова думка, 1985. – 268 с.
- Шидловский А.К., Вагин Г.Я., Куренный Э.Г. Расчеты электрических нагрузок систем электроснабжения промышленных предприятий. – М.: Энергоатомиздат, 1992. —224 с.
- Курінний Е. Г., Циганкова Н.В. Імітація корельованних випадковіх процесів в електричних мермжах методом елементарних процесів. – Праці Донецького держ. техн. ун–ту. Серія "Електротехніка і енергетика", випуск 17. – Донецьк: ДонНТУ, 2000. – с. 242—245.
- Жежеленко И.В., Саенко Ю.Л. Качество электроэнергии на промышленных предприятиях. – М.: Энергоатомиздат, 2005. – 261 с.