ОПТИМИЗАЦИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПЕТЛЕВОГО ФИЛЬТРА КОНТУРА ФАПЧ С АСТАТИЗМОМ ВТОРОГО ПОРЯДКА СИСТЕМ СИНХРОНИЗАЦИИ СПУТНИКОВЫХ КОМАНДНО-ПРОГРАММНЫХ РАДИОЛИНИЙ

Слесарев А.С.
Источник:
вестник РГРТУ, Рязань, 2007, №22.

Введение. Одним из основных элементов систем фазовой синхронизации приемников спутниковых командно-программных радиолиний (КПРЛ) является контур фазовой автоподстройки частоты (ФАПЧ). Современные КПРЛ характеризуются низким отношением сигнал-шум, наличием изменяющегося во времени доплеровского сдвига частоты и других мешающих факторов, что обуславливает рост фазовой ошибки в контуре ФАПЧ [1]. Поэтому задача повышения устойчивости контура ФАПЧ систем синхронизации спутниковых КПРЛ к действию мешающих факторов в настоящее время весьма актуальна.

К современным системам фазовой синхронизации спутниковых КПРЛ предъявляются противоречивые требования по уменьшению ошибки слежения и снижению времени установления режима синхронизма. Это приводит к необходимости оптимизации контура ФАПЧ по нескольким показателям качества, включающим фазовую ошибку и время установления режима синхронизма. Кроме того, широкий диапазон изменения условий работы приемников спутниковых КПРЛ обуславливает потребность в придании робастных свойств системе фазовой синхронизации.

В [2, 3] приводятся результаты синтеза оптимального петлевого фильтра контура ФАПЧ при наличии аддитивного белого шума и постоянного доплеровского сдвига частоты, приводящего к системе с астатизмом 2-го порядка, а также при линейно изменяющемся доплеровском сдвиге, что приводит к системе с астатизмом 3-го порядка. Достоинство системы ФАПЧ 3-го порядка – нулевое значение установившейся динамической ошибки по фазе при линейном изменении частоты Доплера. Однако такие системы, в отличие от систем ФАПЧ с астатизмом 2-го порядка, не всегда устойчивы и более сложны в анализе [1], поэтому часто используются системы ФАПЧ с астатизмом 2-го порядка.

Цель работы – оптимизация передаточной функции петлевого фильтра контура ФАПЧ с астатизмом 2-го порядка по нескольким показателям качества, а также обеспечение робастности к изменению условий приема.

Обоснование показателей качества контура ФАПЧ. В современных космических КПРЛ чаще всего используются фазоманипулированные (ФМн) сигналы. Система синхронизации приемника ФМн-сигналов содержит контур ФАПЧ в виде петли Костаса [4]. На рисунке 1 представлена структурная схема линейной модели петли Костаса.

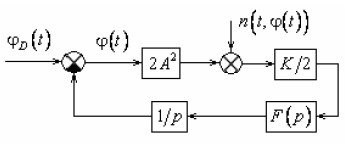
Рисунок 1 – Структурная схема линейной модели петли Костаса

Структурная схема, представленная на рисунке 1, описывается следующим уравнением:

           (1)

где φ(t)) – фазовая ошибка в контуре ФАПЧ, φ_D(t)) – сумма начальной фазы, фазы за счет постоянной и линейно изменяющейся составляющих доплеровского сдвига частоты ФМн-сигнала, K – коэффициент усиления петли, A – амплитуда ФМн-сигнала, F(p) – передаточная функция петлевого фильтра,) n(t, φ(t)) –эквивалентный фазовый шум, спектральная плотность мощности (СПМ) которого равномерна в полосе контура ФАПЧ и зависит от уровня шума и амплитуды A сигнала [4].

Зависимость доплеровского сдвига частоты сигнала спутниковой КПРЛ от времени на периодах, сравнимых с постоянной времени контура ФАПЧ, можно считать линейной, особенно если не рассматривать малые значения угла места спутника. Тогда выражение для фазы (φ_D(t)) принимает вид:

φ_D(t))=φ₀+ω_Dt+ω'_Dt²/2

где φ₀ – начальная фаза ФМн-сигнала, ω_D – постоянная составляющая доплеровского сдвига частоты, ω'_D – скорость линейного изменения доплеровского сдвига частоты.

Петлевой фильтр контура ФАПЧ с астатизмом 2-го порядка представляет собой пропорционально-интегрирующее звено с передаточной функцией [3]:

F(p)=(pα₂+1)/(pα₁)

где α₁ и α₂ – коэффициенты петлевого фильтра.

Из анализа выражения (1) следует, что фазовая ошибка в контуре ФАПЧ складывается из флуктуационной ошибки из-за наличия аддитивного шума и установившейся динамической ошибки вследствие присутствия доплеровского сдвига частоты.

Выражение для дисперсии флуктуационной ошибки в контуре ФАПЧ в виде петли Костаса определяется выражением:

                    (2)

где S_n(ω) – СПМ эквивалентного фазового шума n(t, φ(t)). При увеличении отношения сигнал-шум уровень S_n(ω) повышается, увеличивая σ_φ²

φ_S=ω'_D∙α₁/(KA²)                                                      (3)

Введем показатель качества, учитывающий обе составляющие фазовой ошибки в контуре ФАПЧ:

δ_с=σ_φ+φ_S                                                           (4)

Другим показателем качества контура ФАПЧ является время установления режима синхронизма, которое в случае астатизма 2-го порядка может быть оценено с помощью выражения [1]:

t_S≈16 α₁/(K α₂(1+ α₁/(Kα₂²)))                                             (5)

Таким образом, для повышения устойчивости контура ФАПЧ с астатизмом 2-го порядка системы синхронизации приемника спутниковой КПРЛ необходимо произвести оптимизацию коэффициентов α₁ и α₂ петлевого фильтра по двум показателям качества: δ_си t_S. Данные показатели качества имеют стандартный вид, т.е. являются неотрицательными, и качество контура ФАПЧ обратно пропорционально δ_с и t_S [5].

Обоснование критерия оптимальности. Поскольку производится оптимизация по двум показателям качества, вводится результирующий показатель качества kr в виде взвешенной суммы [5]:

kr=λδ_{с норм}+(1-λ) t_{S норм}                                            (6)

где λ – весовой коэффициент; δ_{с норм}=δ_с/δ_{с max}; t_{S норм}=t_S/t_{S max}; δ_{с max} и t_{S max} – максимально допустимые значения показателей качества δ_с и t_S соответственно. Исходя из линейности модели контура ФАПЧ было выбрано значение δ_{с max}=30˚ [4], а из типовых характеристик контуров ФАПЧ КПРЛ – t_{S max}=0,4 c. Выбор значения λ является субъективным и зависит от особенностей применения конкретной КПРЛ. В данной работе важность обоих показателей качества контура ФАПЧ считалась одинаковой, поэтому λ=0,5.

Поскольку результирующий показатель качества kr имеет стандартный вид, соответствующий ему критерий оптимальности определяется выражением:

kr _min=min_(α1,α1)(λδ_{с норм}(α₁, α₂)+(1-λ) t_{S норм}(α₁, α₂)                (7)

Оптимизация коэффициентов петлевого фильтра. В соответствии с критерием оптимальности (7) наилучшими являются значения коэффициентов α₁ и α₂ петлевого фильтра, обеспечивающие минимум результирующего показателя качества kr. С этой целью для различных значений отношения сигнал-шум в соответствии с выражениями (2)-(6) были рассчитаны зависимости δ_с от t_S, а затем определена пара значений δ_с и t_S, минимизирующая величину kr. На рисунке 2 приведены рассчитанные зависимости результирующего показателя качества kr. от времени установления режима синхронизма t_S при различных значениях отношения сигнал-шум q, при этом ось ординат имеет логарифмический масштаб.

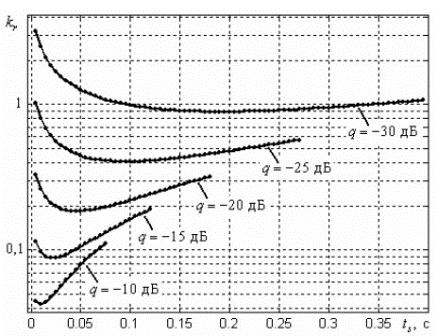
Рисунок 2 – Зависимости результирующего показателя качества от времени установления режима синхронизма

Расчет производился при значении скорости линейного изменения доплеровского сдвига частоты ω'_D=60 рад/c², являющегося типичным для среднеорбитальных спутниковых систем связи (ELLIPSO, Inmarsat, Odyssey) при малоподвижном наземном приемопередатчике. Как следует из анализа зависимостей, повышение отношения сигнал-шум q приводит к уменьшению времени вхождения в синхронизм t_S и снижению оптимального значения результирующего показателя качества kr, а значит, и фазовой ошибки в контуре ФАПЧ.

Повышение устойчивости контура ФАПЧ к изменению отношения сигнал-шум. Приемники спутниковых КПРЛ часто функционируют в условиях априорной неопределенности относительно значения отношения сигнал-шум. В связи с этим требуется выбрать значения коэффициентов α₁ и α₂ петлевого фильтра контура ФАПЧ, обеспечивающие робастность к изменению отношения сигнал-шум.

На рисунке 3 представлены зависимости результирующего показателя качества kr от отношения сигнал-шум для коэффициентов α₁ и α₂ петлевого фильтра контура ФАПЧ, оптимизированных для различных значений отношения сигнал-шум. При этом через α_1,2onm(q=L дБ) обозначена зависимость, построенная для петлевого фильтра, коэффициенты которого оптимизированы для отношения сигнал-шум L дБ. При усреднении каждой зависимости по всему диапазону отношений сигнал-шум минимальное среднее значение результирующего показателя качества kr получено для α_1,2onm(q=-25 дБ).

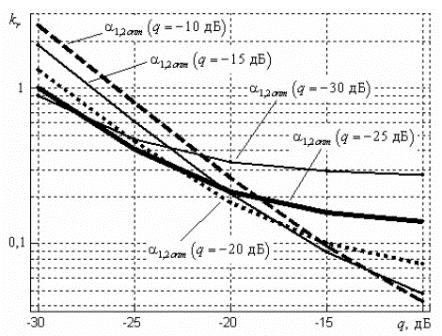
Рисунок 3 – Зависимости результирующего показателя качества от отношения сигнал-шум

Таким образом, использование коэффициентов петлевого фильтра контура ФАПЧ с астатизмом 2-го порядка, оптимальных для отношения сигнал-шум -25 дБ, позволяет достичь наилучшей устойчивости к изменению отношения сигнал-шум в диапазоне от -30 дБ до -10 дБ, характерном для приемников КПРЛ со слабонаправленными антеннами в нормальных условиях, а также при ослаблении сигнала вследствие наличия препятствий, замираний и т.д.

Заключение. Таким образом, обоснован критерий оптимальности контура ФАПЧ с астатизмом 2-го порядка спутниковых КПРЛ при наличии линейно изменяющегося доплеровского сдвига частоты сигнала. Произведена оптимизация коэффициентов петлевого фильтра, осуществлен выбор коэффициентов, обеспечивающих устойчивость к изменению отношения сигналшум в диапазоне от -30 дБ до -10 дБ.

Библиографический список

1. Цифровые радиоприемные системы: Справочник / Под ред. М.И. Жодзишского. – М.: Радио и связь, 1990. – 208 с.
2. Tausworthe R.C. A Second/Third Hybrid Phase-Locked Receiver for Tracking Doppler Rates. – JPL Technical Report 32-1526, Vol. 1.
3. Tausworthe R.C. Theory and Practical Design of Phase-Locked Receivers. – JPL Technical Report 32-819, Vol. 1, 1966.
4. Линдсей В. Системы синхронизации в связи и управлении. – М.: Сов. радио, 1978. – 600 с.
5. Гуткин Л.С. Оптимизация радиоэлектронных устройств по совокупности показателей качества. – М.: Сов. радио, 1975. – 368 с.

вверх

---

© Nesterenko Ann, 2011