RUS
| ENG
||
ДонНТУ
Портал
магістрів ДонНТУ

Носов Сергій Сергійович
Факультет комп'ютерних наук і технологій
Кафедра комп'ютерних систем моніторингу
Спеціальність: Комп'ютерний еколого-економічний моніторинг
Науковий керівник: Бєловодський Валерій Миколайович
Матеріали до теми випускної роботи: Про автора
Реферат з теми випускної роботи
Розробка кінцевої математичної моделі динаміки метеопараметрів і прогнозування їх поведінки на її основі
Актуальність теми
Однією з важливих сучасних проблем людства є достовірний прогноз погоди.
Нерідко, прогноз погоди здійснюється з метою урахування можливих негативних і катастрофічних впливів на людську діяльність і зазвичай
здійснюється з певною часткою достовірності. Для зберігання вихідних даних спостережуваних метеопоказників необхідне створення
однієї великої або декількох, розподілених за територіальниою або іншою ознакою, порівняно менших баз даних для збору інформації,
її належної обробки та здійснення прогнозу. Зазвичай, це дозволяє своєчасно реагувати на прогноз і приймати відповідні заходи.
Особливо помітний економічний ефект дає використання метеорологічної інформації в таких сферах діяльності, як авіація, будівництво, рибальство, енергетика, судноплавство, а також сільське господарство.
З наукової точки зору, прогнозування погоди - одна з найбільш складних задач фізики атмосфери. Удосконалення комп'ютерного обладнання дозволяє реалізовувати математичні підходи та методи дослідження атмосфери. Кожен з них дозволяє в тій чи іншій мірі прогнозувати метеопоказники.
Таким чином, тема і результати дослідження в області прогнозування динаміки метеопараметрів зумовлюються рішенням задачі прогнозу спостережуваних метеопараметрів.
Формулювання завдань
Мета магістерської роботи - розробити кінцеву математичну модель динаміки для прогнозування метеопараметрів у вигляді програмного продукту, що включає в себе ряд сучасних методів попередньої підготовки та складання прогнозів метеорологічних даних.
Об'єктом дослідження є часові ряди спостережуваних метеопараметрів: температура, вологість, тиск, швидкість вітру.
Предмети дослідження - методи попередньої підготовки і прогнозування даних, якість і дальність результатів прогнозу.
Гіпотеза дослідження - процес складання прогнозу буде проходити успішніше і продуктивніше за наступних умов:
1. Використання сучасних методів при роботі з тимчасовими рядами, таких як метод Еглайса [1], метод головних компонент [2], експоненціальне згладжування [3], критерій Ірвіна [3], лінійна інтерполяція [4];
2. Огляд існуючих методів і підходів, що використовуються для прогнозу метеопараметрів: виявлення переваг та недоліків; пропонування власної методики (математичної моделі);
3. 3. Програмна реалізація, впровадження в практику запропонованої математичної моделі.
Таким чином, завдання магістерської роботи наступні:
1. Вивчити існуючі методи попередньої підготовки і прогнозу тимчасових рядів, і впровадити їх в існуючий прогностичний комплекс;
2. Виконати огляд існуючих методів і походів прогнозування;
3. Розробити математичну модель динаміки метеопараметрів;
4. Провести апробацію математичної моделі;
5. Реалізувати програмно запропоновану модель;
6. Забезпечити інформаційний захист програмної математичної моделі.
Наукова значимість роботи
Виходячи з мети проведення прогнозу метеопоказників, важливе значення має його достовірність, яка, частково, визначається надійністю вихідних даних, важливим є завдання попереднього аналізу даних, з метою виключення, по можливості, випадкових шумів або, навпаки, заповнення відсутніх даних.
Наукова значимість (новизна) роботи з'являється у двох випадках:
- Вирішення старого завдання новими методами;
- Вирішення нового завдання старими методами.
Наукова значимість даної роботи полягає у використанні нових підходів до вирішення задачі прогнозування динаміки метеорядов, зокрема використання:
- Інтерполяційних методів на першому етапі роботи, для початкового навчання часового ряду;
- Методів визначення найменшої розмірності моделі, таких як метод помилкових сусідів і
“Гусениця”, що забезпечує однозначність прогнозу;
- Методу Еглайса для формування прогностичної моделі.
Результати реалізації використаних в роботі підходів планується порівняти з результатами, отриманими при здійсненні прогнозу за допомогою прогностичного комплексу.
Вагомість перерахованих явищ на кінцеві результати прогнозування досить істотна, тому нижче, на базі відомих методів, формулюються тези про практичну цінність магістерської роботи.
Практична цінність результатів роботи
Практична цінність роботи полягає в тому, що одержувані результати мають практичну спрямованість. У даній магістерській роботі таким практичним завданням є формування прогнозу.
Так, при проведенні чисельних експериментів по попередній підготовці часового ряду, в залежності від набору вихідних даних, відносна похибка відновлення пропущених значень становила близько 12%. Попередня підготовка є першим етапом пропонованої кінцевої математичної моделі, і дозволяє підвищити точність прогнозу внаслідок відсутності аномальних значень і прогалин у цих часових метеорядях.
Розроблювані і пропоновані методики обробки часових рядів, пропоновані способи прогнозування спрямовані, в кінцевому рахунку, на підвищення якості прогнозу. Практична цінність полягає у вирішенні завдання, що має практичну спрямованість, а саме: підвищення точності прогнозу.
Огляд предметної області досліджень за темою в ДонНТУ
Побудова математичної моделі динаміки заснована на обробці тимчасових метеорядов, отриманих з метеостанції Vantage Pro 2, встановленої на кафедрі КСМ факультету КНТ ДонНТУ. Дана метеостанція дозволяє знімати дані по наступних метеорологічним показниками:
- Температура;
- Вологість;
- Тиск;
- Швидкість вітру.
На даний момент на кафедрі КСМ вже розроблений програмний продукт, основою якого була розробка методики короткострокового прогнозу спостережуваних метеопоказників по часових рядах метеопараметорів [5]. Він дозволяє на основі рядів, що знімаються з метеостанції, здійснювати короткострокове прогнозування температури, вологості, тиску та швидкості вітру.
Всі дані за спостережуваними метеопоказниками зберігаються на сервері кафедри КСМ та апаратно-програмному комплексі екологічного моніторингу атмосферного повітря “АКІАМ”. Інтервал поміж вимірами метеопараметрів становить 10 хвилин [6]. Таким чином, в процесі експлуатації бази даних постійно формується і поступово накопичується сукупність тимчасових рядів. Наявність цієї інформації робить цілком реальним завдання розробки математичної моделі динаміки часових рядів в рамках досліджень в області здійснення прогнозу погоди, з використанням математичних методів і середовищ розробки для програмної реалізації виконаної роботи.
За темою магістерської роботи в даній предметній області проводилися дослідження в ДонНТУ і в попередні роки магістрами спеціальності КЕМ:
- Повзло Сергій Олексійович “Розробка системи моніторингу метеопараметрів атмосфери з використанням інструментальних засобів, що працюють в реальному масштабі часу” (2006 рік). Науковий керівник Аверін Геннадій Вікторович;
- Іващенко Алеся Борисівна “Чисельний аналіз математичних моделей прогнозу погоди” (2006 рік). Науковий керівник Бєловодський Валерій Миколайович;
- Гриценко Анна В'ячеславівна
“Прогнозування погодних умов за часовими рядами метеорологічних показників” (2010 рік). Науковий керівник Бєловодський Валерій Миколайович;
- Сивяков Артем Сергійович “Побудова прогностичного комплексу та впровадження його в електронну мережу університету” (2011 рік). Науковий керівник Бєловодський Валерій Миколайович.
Огляд предметної області досліджень у світі
За останні десятиріччя у світі використовується ряд методів для прогнозу погоди. Умовно їх можна розділити на наступні:
– Синоптичні методи - засновані на аналізі погодних карт. Сутність цих методів полягає в одночасному огляді стану атмосфери на великій території, що дозволяє визначити характер розвитку атмосферних процесів і подальшу зміну погодних умов [7];
– Чисельні методи - засновані на математичному рішенні систем повних рівнянь гідродинаміки та отриманні прогностичних полів тиску, температури на певні проміжки часу. Точність чисельних прогнозів залежить від швидкості розрахунку обчислювальних систем, від кількості та якості інформації, що надходить з метеостанцій [7];
– Анасамблеві піходи - засновані на припущенні про наявність невизначеності у відомостях про стан атмосфери. Ансамблеве прогнозування є чисельним методом прогнозування, що використовується для спроби створення репрезентативної вибірки з можливих майбутніх станів динамічної системи. Ансамблеве прогнозування є однією з форм аналізу Монте Карло: складається декілька чисельних прогнозів (з рядом незначною мірою відрізнених початкових умов), що є цілком правдоподібними, враховуючи набір минулих і нинішніх спостережень або вимірювань. Якщо ансамбль добре побудований, то його прогнози охоплять весь діапазон можливих результатів, включаючи ряд утворень, де можуть зростати невизначеності [8];
– Методи нелінійної динаміки. У рамках даних методів отримано ряд фундаментальних теоретичних результатів і розроблені методики, що обґрунтовують принципову можливість прогнозування фізичних процесів на базі їх тимчасових рядів. Теоретичним фундаментом цих розробок і методів є теорема Такенса. Однією з його основоположних ідей є те, що при побудові емпіричних моделей за часовим рядом як відсутніх змінних можна використовувати або послідовні значення доступною спостерігається величини, або її послідовні похідні. Було доведено, що при реконструкції за скалярною тимчасовою реалізацією динамічної системи і метод часових затримок, і метод послідовних похідних гарантують, що в нових змінних буде отримано еквівалентну опис вихідної динамічної системи при досить великій розмірності відновлених векторів D. А саме, повинна виконуватися умова D>2d, де d - розмірність множини M в фазовому просторі вихідної системи, на якому відбувається моделюємий рух [9]. Ці твердження складають зміст теорем Такенса.
– Статистичний метод - передбачає прогнозування погоди на основі деякої статистики, з якої формується часовий ряд, і проводиться реконструкція (відновлення) рівнянь. Відмінність від методів нелінійної динаміки полягає в тому, що в якості тхи даних використовуються значення, обчислені на основі рівняння, складеного на основі деякої статистики спостережуваної величини. Найпростіші методи відновлення, використовувані для прогнозування залежності, виходять із заданого часового ряду, тобто функції, визначеної в кінцевому числі точок на осі часу. Тимчасовий ряд при цьому часто розглядається в рамках тієї чи іншої ймовірнісної моделі. Він може бути багатовимірним. Основні розв'язувані завдання - інтерполяція і екстраполяція. Можуть виявитися корисними попереднє перетворення змінних, наприклад, логарифмування. Найбільш часто використовується метод найменших квадратів при декількох чинниках. Метод найменших модулів, сплайни та інші методи екстраполяції застосовуються менш часто, хоча їх статистичні властивості в деяких випадках краще [10].
Для оцінки точності прогнозу використовуються ймовірнісно-статистичні моделі відновлення залежності, наприклад, будується найкращий прогноз за методом максимальної правдоподібності. Існують параметричні (зазвичай на основі моделі нормальних помилок) та непараметричні оцінки точності прогнозу і довірчі межі для прогнозу (на основі Центральної Граничною Теореми теорії ймовірностей). Застосовуються також евристичні прийоми, які не засновані на ймовірнісно-статистичної теорії: метод ковзних середніх, метод експоненціального згладжування. Зазначені методи не є методами прогнозу, однак можуть використовуватися для оцінки його точності [11].
Зміст роботи по етапах
Етап 1. Попередня підготовка часового ряду.
1. Перегляд на наявність прогалин і їх заповнення (у разі виявлення).
На даному етапі попередньої обробки прогалини в даних генерувалися в тренувальному часовому ряду температури псевдовипадковим чином. Кожне значення часового ряду могло виявитися нульовим з деякою ймовірністю. Таким чином, у вихідному, тренувальному ряду утворювалися порожнечі різної довжини. Усунення порожнеч здійснювалося різними методами, в залежності від довжини утворюваних прогалин. Так, якщо довжина прогалин у цих була одиничною, та прогалини розташовувалися не по краях ряду, то пропущені значення замінялися середнім арифметичним їх сусідніх значень. Інакше використовувався метод лінійної інтерполяції, з деякими варіаціями. Залежно від місця розташування пробілу в даних, використовувалася лінійна інтерполяція “вперед”, “назад”, “нейтральна”. У розрахункових співвідношеннях лінійної інтерполяції “нейтральної” для отримання пропущених значень використовувались значення до і після прогалин в даних, а також їх індекси. Якщо використовувалася лінійна інтерполяція “вперед”, то в розрахункових співвідношеннях використовувалися значення перед пропуском в даних та їх індекси. У разі застосування лінійної інтерполяції “назад” проводилися аналогічні інтерполяції “вперед” за винятком використання в розрахункових співвідношеннях значень, що йдуть після прогалин в даних. Залежно від наявності пропусків на кінцях ряду, виконувалося комбінування методів. Отримані значення усереднювались, в залежності від кількості застосовуваних методів.
2. Повторний перегляд, виявлення і коректування аномальних значень.
Виявлення аномальних значень здійснювалося з використанням критерію Ірвіна. А їх подальше коректування здійснювалася методом лінійної інтерполяції (у разі аномалій, що мають довжину більше одиниці), що дозволяло замінити аномальні значення часового ряду значеннями, відповідними динаміці ряду. Так, наприклад, якщо на певному проміжку значення часового ряду зростали, то мала місце деяка тенденція і значення, на яке було замінено аномальне, відповідало еволюції певного проміжку ряду. У випадку з убиваючими значеннями ряду проводилися аналогічні операції. Аномальні значення тимчасових рядів одиничної довжини замінялися середнім арифметичним сусідніх значень.
3. Остаточний перегляд, згладжування.
Використання методу експоненціального згладжування стосовно отриманому, в результаті виконання другого етапу, часовому ряду. А саме до тих значень, які були отримані в результаті заміни аномальних значень новими. При згладжуванні, значенням поточного згладженого значення
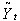 була функція від поточних не згладженого значення
була функція від поточних не згладженого значення  і попереднього згладженого
і попереднього згладженого  :
:
 ,
,
де 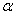 – параметр згладжування, причому
– параметр згладжування, причому 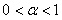 [12].
[12].
Вибір значення параметра згладжування вироблялося за допомогою складеного в середовищі розробки Visual Studio 2008 Professional програмного забезпечення. Пошук найкращого значення 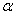 здійснювався в діапазоні
здійснювався в діапазоні 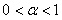 з кроком 0.0001: значення
з кроком 0.0001: значення 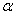 , за якого середньоквадратичне відхилення було мінімальним, вважалося найкращим. Вибране значення приймалося в якості найкращого і використовувалося при подальших розрахунках [12]. Результати згладжування виявилися задовільними, так як отриманий часової ряд не містив шумових складових.
, за якого середньоквадратичне відхилення було мінімальним, вважалося найкращим. Вибране значення приймалося в якості найкращого і використовувалося при подальших розрахунках [12]. Результати згладжування виявилися задовільними, так як отриманий часової ряд не містив шумових складових.
Вихідний часовий ряд зчитувався з файлу і завантажувався у пам'ять програми:
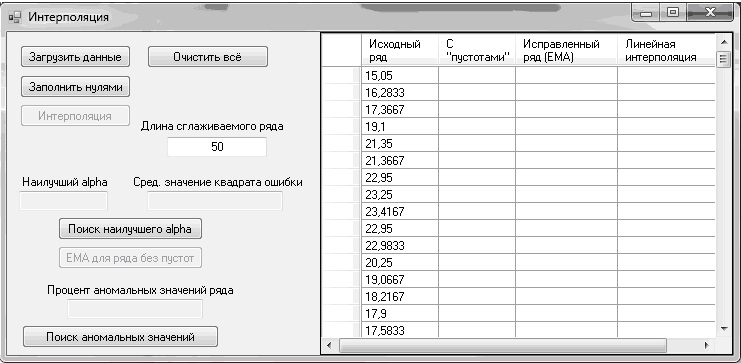
Малюнок 1 - Вихідний часовий ряд
Далі, вибиралося значення довжини загладжуваного ряду (наприклад, 50),
вихідні дані заповнювалися пробілами (натисканням на відповідні кнопки). Був отриманий результат чисельного експерименту
по попередній підготовці часового ряду, що містить:
- Результат пошуку найкращого значення параметра згладжування;
- Середнє значення квадрата помилки;
- Відсоток аномальних значень для 50 перших значень часового ряду [12]:

Малюнок 2 - Результат чисельного експерименту
Результат виконання етапу № 1 - підданий попередній підготовці часовий ряд.
Етап 2. Вибір розмірності моделі.
Для вирішення цього завдання використовуються різні методи оцінки:
неправдивих сусідів, головних компонент, Грассбергера - Прокаччіа, метод добре пристосованого базису.
Застосовується метод помилкових сусідів для визначення найменшої розмірності моделі, що забезпечує однозначність прогнозу.
Метод “Гусениця” є процедурою перетворення одновимірного часового ряду в багатовимірний.
Метод помилкових сусідів заснований на перевірці тієї властивості, що фазова траєкторія,
відновлена в просторі достатньої розмірності не повинна мати само перетинів. За пробної розмірності D для кожного відновленого вектора
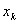 здійснюється пошук одного (найближчого) сусіда; збільшивши D на 1, визначають, які з сусідів виявилися хибними
(сильно розійшлися), а які - справжніми. Підраховують відношення числа помилкових сусідів до загальної кількості відновлених векторів.
Якщо при збільшенні D це число стає малим при деякому значенні D*, то останнє і є оцінкою розмірності простору,
в якому досягається вкладення траєкторії модельованого руху [6].
здійснюється пошук одного (найближчого) сусіда; збільшивши D на 1, визначають, які з сусідів виявилися хибними
(сильно розійшлися), а які - справжніми. Підраховують відношення числа помилкових сусідів до загальної кількості відновлених векторів.
Якщо при збільшенні D це число стає малим при деякому значенні D*, то останнє і є оцінкою розмірності простору,
в якому досягається вкладення траєкторії модельованого руху [6].
Існує ряд алгоритмів, які є реалізацією методу “Гусениця”. Базовий алгоритм складається з чотирьох послідовних етапів. При цьому розглядається часовий ряд
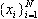 , утворений послідовністю N рівновіддалених значень деякої (можливо, випадкової) функції f(t):
, утворений послідовністю N рівновіддалених значень деякої (можливо, випадкової) функції f(t):
xi = f((i-1)*D*t),
де i = 1,2,…,N.
Розглянемо більш детально кожен етап.
Крок № 1 (Розгортка одновимірного ряду в багатовимірний).
Вибирається деяке число M < N, що називають довжиною гусениці, і представляються перші M значень послідовності f
в якості першого рядка матриці X. В якості другого рядка матриці беруться значення послідовності з x2 по xM+1.
Останнім рядком з номером k = N – M + 1 будуть останні M елементів послідовності.
У загальному випадку, вибір довжини гусениці М істотно залежить від завдання,
розв'язуваної цим методом. Найбільш типові і досліджені розробниками методу випадки:
1. Якщо вирішується завдання аналізу вихідного часового ряду, наприклад, з метою відшукання прихованих періодів з невідомими періодами, то можна використовувати значення довжини гусениці М, що дорівнює половині довжини ряду N:
М = N / 2.
Якщо часовий ряд довгий, то значення М вибирається таким, яке дозволяє використовувати комп'ютерні ресурси;
2. Якщо вирішується більш вузьке завдання, наприклад, згладжування вихідного часового ряду або виділення періодичності з відомим періодом, то працює інший механізм, пов'язаний з методом “Гусениця” - механізм фільтрації. Слід зазначити, що при виборі довжини гусениці М повинна виконуватися умова: M < N;
3. Якщо вирішується завдання найкращого виділення (або виключення) періодичного, але не обов'язково гармонійного, коливання з відомою частотою і, отже, періоду. У цьому випадку буває необхідно для кращого вирішення завдання зменшити довжину часового ряду N. Періодичні коливання найкращим чином виділяються, якщо М і N кратні довжині періоду, в якому виділяється коливання.
Далі, відповідно до даної схеми (за винятком стандартизації ознак), проводиться аналіз головних компонент (АГК).
Таким чином, вибране значення M є початковим. Далі використовується метод головних компонент для остаточного його визначення.
Крок №2. (Аналіз головних компонент: сингулярне розкладання вибіркової коваріаційної матриці)
Спочатку обчислюється матриця V = (1/k)XTX, де k = N – M + 1 – обсяг вибірки. Незважаючи на те, що її елементи не центровані, далі матриця V називається коваріаційною, іноді - нецентральною коваріаційною.
Наступний крок полягає в обчисленні власних чисел і власних векторів матриці V, тобто її розкладання V = PLPT,
де L – діагональна матриця, на діагоналі якої стоять впорядковані за спаданням власні числа, а P - ортогональна матриця власних векторів матриці V.
Матриці L і P спільно мають безліч інтерпретацій, заснованих на АГК. Зокрема, матрицю P можна розглядати як матрицю переходу до головних компонентів
XP = Y = (y1,y2,...,yM).
При виборі довжини гусениці, що дорівнює N – M + 1, власні вектора і головні компоненти (з точністю до нормування) міняються місцями.
Крок №3. (Відбір головних компонент)
З огляду властивостей матриці P можна представити матрицю ряду X як X = Y PT. Таким чином, виходить розкладання матриці на ряди за ортогональними складовими (головних компонентів).
У той же час перетворення 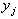 = X
= X є лінійним перетворенням вихідного процесу за допомогою дискретного оператора згортки, тобто:
є лінійним перетворенням вихідного процесу за допомогою дискретного оператора згортки, тобто:

Таким чином, процедура “Гусениця” породжує набір лінійних фільтрів, налаштованих на складові вихідного процесу. При цьому власні вектори матриці V виступають в ролі перехідних функцій відповідних фільтрів.
Візуальне і аналітичне вивчення, як власних векторів, так і головних компонент, отриманих в результаті лінійної фільтрації, може дати інформацію про структуру досліджуваного процесу і властивості складових його додатків.
Зокрема, серед головних компонент можна виділити:
1. Пов'язані з трендом (повільно мінливі);
2. періодичні;
3. шумові.
Для знаходження періодичних складових надзвичайно велику візуальну інформацію дає вивчення двовимірних графіків, аналогічних фігурам Ліссажу, коли по осях x і y відкладаються різні пари власних векторів або головних компонент.
Крок №4. (Відновлення одновимірного ряду)
Наступним ключовим елементом методу “Гусениця” є процедура відновлення. Ця процедура заснована на розкладанні
X = Y PT. Відновлення проводиться з даного набору головних компонентів, якщо при застосуванні формули відновлення
X = Y* PT матриця Y* отримана з матриці Y обнулінням всіх, що не входять в набір головних компонент. Таким чином, можна отримати наближення матриці ряду, що нас цікавить, або частини цієї матриці. Перехід до вихідного ряду формально може бути здійснений усередненням матриці ряду по побічних діагоналях і може призвести до деякого спотворення отриманої структури.
При програмній реалізації етапи наведеного вище алгоритму не відтворюються безпосередньо. Наприклад, етап побудови матриці X відсутній, а формули перетворені до вигляду, зручного для проведення прискорених обчислень.
Основним параметром методу є M – довжина гусениці.
При геометричній інтерпретації цей параметр є розмірністю простору, в якому досліджується траєкторія багатовимірної ламаної лінії, в яку переводиться вихідний часовий ряд методом “Гусениця”. Максимальним значенням
М є M <= N / 2,
оскільки розмірність множини k точок (вершин ламаної) в M - мірному просторі не перевершує min(M,k-1).
Цей підхід тісно пов'язаний з аналітичною інтерпретацією методу “Гусениця” як апроксимацією рішення рівняння в кінцевих різницях з l коефіцієнтами.
Можна сказати, що l – це число ступенів свободи функції f(t), а отже, і відповідного їй часового ряду. У методі “Гусениця” це виразиться в тому, що
M > l у коваріаційної матриці виявиться тільки l ненульових власних чисел (з огляду на обмежену точність обчислень, решта
M-l будуть майже нульовими). Однак, в реальних дослідженнях, ця ситуація є досить рідкісною.
Результат виконання етапу № 2 - цілочисельне значення - розмірність моделі, яка повинна бути меншою, ніж довжина часового ряду (згідно методу “Гусениця”).
Етап 3. Формування прогностичних моделей.
На даному етапі роботи проводиться формування прогностичних моделей, з використанням методу Еглайса (для отримання оператора еволюції), доцільність використання якого полягає в необхідності синтезу рівняння регресії.
Даний метод полягає в наступному. Нехай є інформація про об'єкт, задана у вигляді таблиці, де кожній точці в просторі параметрів відповідає певний відгук. Потрібно синтезувати відповідне рівняння регресії у вигляді
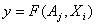 , де {
, де {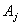 } – набір коефіцієнтів рівняння регресії, {
} – набір коефіцієнтів рівняння регресії, {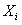 } – набір параметрів об'єкта [13].
} – набір параметрів об'єкта [13].
Алгоритм формування регресійного рівняння розбивається на наступні етапи:
1. Формування банку елементарних функцій {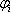 }. Вони задаються у вигляді:
}. Вони задаються у вигляді:
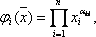
де n – число параметрів об'єкта, 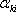 - різноманітні набори позитивних і негативних чисел. Причому
- різноманітні набори позитивних і негативних чисел. Причому
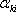 обмежено наступною умовою:
обмежено наступною умовою:
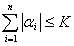 .
.
Передбачається, що K задається користувачем. Кожна функція представляється у вигляді масиву ступенів їх аргументів.
2. Відбір банку перспективних, в деякому сенсі, функцій.
На цьому етапі, з використанням методу найменших квадратів, здійснюється відбір функцій, що дають мінімальне відхилення.
3. почергове вилучення (елімінація) відібраних функцій і синтез регресійного рівняння.
Зміст останньої етапу полягає в наступному. Можна вважати, що серед відібраних функцій лише частина необхідна в синтезованому рівнянні регресії. Решту з банку відібраних функцій необхідно вилучити. Нехай відібрано, наприклад, всього p перспективних функцій. Тоді є p варіантів вилучення однієї функції зі складу перспективних. Для всіх функцій банку за методом найменших квадратів обчислюються коефіцієнти елементарних рівнянь регресії у вигляді
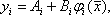 а також визначаються сумарні квадратичні відхилення:
а також визначаються сумарні квадратичні відхилення:
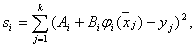
де  . Потім обчислюється відповідне середньоквадратичне відхилення
. Потім обчислюється відповідне середньоквадратичне відхилення 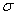 і виробляється побудова
і виробляється побудова 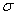 (i) на діаграмі елімінації. Доки з рівняння регресії виключаються несуттєві функції, доти
(i) на діаграмі елімінації. Доки з рівняння регресії виключаються несуттєві функції, доти
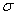 змінюється мало. Коли ж залишаються суттєві функції, то виключення будь-якої з них помітно збільшує середньоквадратичне відхилення
змінюється мало. Коли ж залишаються суттєві функції, то виключення будь-якої з них помітно збільшує середньоквадратичне відхилення 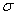 .
Тому, злам на діаграмі елімінації свідчить про отримання найбільш пріоритетним рівняння регресії [13].
.
Тому, злам на діаграмі елімінації свідчить про отримання найбільш пріоритетним рівняння регресії [13].
Таким чином, рівняння регресії, синтезоване за допомогою методу Еглайса, представляється алгебраїчним многочленом (поліномом):
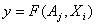 ,
,
де {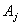 } – набір коефіцієнтів рівняння регресії,
} – набір коефіцієнтів рівняння регресії, 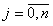 , {
, {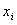 } – набір параметрів об'єкта,
} – набір параметрів об'єкта,
 , n – розмірність моделі, отримана на попередньому етапі. Ступінь полінома К спочатку роботи методу Еглайса задається користувачем, але, в кінцевому рахунку, визначається номером точки зламу на діаграмі елімінації, тобто при почерговому виключення з банку перспективних функцій.
, n – розмірність моделі, отримана на попередньому етапі. Ступінь полінома К спочатку роботи методу Еглайса задається користувачем, але, в кінцевому рахунку, визначається номером точки зламу на діаграмі елімінації, тобто при почерговому виключення з банку перспективних функцій.
Результат виконання етапу № 3 - оператор еволюції (динаміки) тимчасових рядів - регресійне рівняння, обмежене розмірністю моделі, отриманої на попередньому етапі.
Етап 4. Проведення експериментів
1. 1. Підгонка моделі.
Прогнозується динаміка часового метеоряду: значення розраховуються на основі отриманого в пункті 2 етапи 3 оператори еволюції.
2. Діагностична перевірка моделі.
Проводиться порівняння отриманих прогнозних значень з відповідними вихідними значеннями часового ряду спостережуваного метеопараметрів шляхом розрахунку відносної похибки (помилка, у відсотках) отриманого результату.
Так, було проведено 48 експериментів на розробленому прогностичному комплексі (в якості прогнозованого метеопараметру була температура), з використанням таких методів:
а) метод головних компонент:
Проведено 24 експерименти. Найкращі результати прогнозу на:
- 1 годину: лінійна - 2, нелінійна - 4, регресійна - 0
- 3 години: лінійна - 2, нелінійна - 0, регресійна - 4
- 6 годин: лінійна - 2, нелінійна - 3, регресійна - 1
- 9 годин: лінійна - 2, нелінійна - 2, регресійна - 2
Підсумок: лінійна - 8, нелінійна - 9, регресійна - 7 [14].
При здійсненні прогнозу із завчасністю в 1 і 6 годин, нелінійна нейронна мережа є найкращою. Регресійна нейронна мережа є найбільш кращою при здійсненні прогнозу із завчасністю 3 години;
б) метод помилкових сусідів:
Проведено 24 експерименти. Найкращі результати прогнозу на:
- 1 годину: лінійна - 3, нелінійна - 1, регресійна - 2
- 3 години: лінійна -1, нелінійна - 2, регресійна - 3
- 6 годин: лінійна - 4, нелінійна - 0, регресійна - 2
- 9 9 годин: лінійна - 3, нелінійна - 1, регресійна - 2
Підсумок: лінійна - 11, нелінійна - 4, регресійна - 9 [14].
При здійсненні прогнозу із завчасністю в 1, 6 і 9 годин, лінійна нейронна мережа є найкращою, випереджаючи за точністю регресійну мережу.
Загальний підсумок (48 експериментів). Найкращі результати:
Лінійна - 19 з 48 - 39,58%
Нелінійна - 13 з 48 - 27,01%
Регресійна - 16 з 48 - 33,3%
Таким чином, найкращою нейронної мережею є лінійна, оскільки в більшості випадків вона забезпечує найбільшу точність прогнозу температури.
3. Придатність моделі.
На підставі попереднього (пункт 2 етапи 4) пункту робиться висновок про придатність моделі для прогнозу значень. Визначається середнє значення квадрата помилки розрахунків, а також мінімум і максимум. Якщо похибка лежить в допустимих межах, то здійснюється перехід до пункту 4 етапи 4, інакше - перехід до другого етапу.
4. Використання моделі.
Здійснюється прогноз динаміки часового ряду спостережуваного метеопараметрів (згідно розрахованого оператора еволюції) з наперед заданою завчасністю (кількість часових проміжків, на які здійснюється прогноз).
Суть даного кроку етапу полягає в наступному.
4.1. За допомогою розробленого прогностичного комплексу вибирається найкраща нейронна мережа;
4.2. Розробляється програмне забезпечення, що реалізують прогнозування метеопоказників із заданою завчасністю, з використанням обраної нейронної мережі і методу Еглайса;
4.3. Проводяться обчислювальні експерименти для різних сезонних проміжків часу (літо, осінь і т.д.);
4.4. Порівнюються результати;
4.5. Формулюються висновки.
В загальному вигляі, передбачувані етапи роботи можна представити наступним чином:
 Малюнок 3 - Схема роботи розробленої математичної моделі
Малюнок 3 - Схема роботи розробленої математичної моделі
(анімація: об'єм - 171 КБ, розмір - 313х452; кількість кадрів - 14;
нескінченне число циклів повторення; затримка поміж кадрами - 30 мс; затримка поміж першим та останнім кадрами - 150 мс)
Етап 5. Програмна реалізація.
Розробка програмного забезпечення, що реалізує розроблену кінцеву математичну модель динаміки метеопараметрів у вигляді додаткового функціоналу до розробленого прогностичного комплексу, з метою збільшення достовірності прогнозу. Проведення серії обчислювальних експериментів для порівняння розробленої моделі з моделями, присутніми в прогностичному комплексі.
Апробація
Результати першого етапу роботи доповідалися на II всеукраїнській науково-технічній конференції студентів, аспірантів та молодих вчених “Інформаційні управляючі системи та комп'ютерний моніторинг” 12-14 квітня 2011р. і опубліковані у відповідному збірнику (с. 119-123) [12].
Висновки
В якості основного завдання розробки кінцевої математичної моделі динаміки метеопараметрів була прийняте завдання доповнення і вдосконалення розробленого прогностичного комплексу, а також адаптація розробленої моделі для лабораторних досліджень. В результаті роботи був проведений аналіз літератури щодо методів попередньої підготовки і прогнозування тимчасових рядів. Був програмно реалізований перший етап роботи математичної моделі, а також проведений ряд обчислювальних експериментів за попередньою підготовкою тимчасових рядів для подальшої роботи з ними. Результати роботи доповідались на II міжнародній конференції студентів, аспірантів та молодих вчених (матеріали: том 1, с.119-123) [12]. Запропонована модель має можливість прогнозування метеопараметрів, за допомогою методів реконструкції модельних рівнянь, заснованих на аналізі тимчасових рядів, для здійснення чисельного прогнозу погоди з метою підвищення якості та завчасності прогнозу.
При написанні даного автореферату магістерська робота ще не завершена. Термін остаточної готовності роботи - грудень 2011 року. Повний текст роботи та матеріали за темою можуть бути отримані у автора або його керівника після зазначеної дати.
Список літератури
1. Эглайс В.О. Аппроксимация табличных данных многомерным уравнением регрессии. –
Вопросы динамики и прочности: Рига, 1981, Вып. 39. – с.120-125.
2. Википедия: свободная энциклопедия. [Электронный ресурс]:
http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D1%8B%D1%85%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82 (15.05.2011).
3. Татаренко С.И. Методы и модели анализа временных рядов: Метод. указания к лабораторным работам. Тамбов: Тамбовский государственный технический университет, 2008. – 19с.
4. Википедия: свободная энциклопедия. [Электронный ресурс]:
http://ru.wikipedia.org/wiki/Линейная_интерполяция (15.05.2011).
5. Гриценко А.В. Реконструкция уравнений и прогнозирование метеопараметров по их временным рядам. – Донецк, ДонНТУ, 2010. – 149с.
6. Сивяков А.С. Построение прогностического комплекса и внедрение его в электронную сеть университета. – Донецк, ДонНТУ, 2010. [Электронный ресурс]:
http://www.masters.donntu.ru/2010/fknt/sivyakov/diss/index.htm (28.04.2011).
7. Онлайн Энциклопедия Кругосвет ПРОЯВЛЕНИЯ СОЛНЕЧНОЙ АКТИВНОСТИ НА ЗЕМЛЕ. [Электронный ресурс]:
http://www.krugosvet.ru/enc/nauka_i_tehnika/astronomiya/PROYAVLENIYA_SOLNECHNO_AKTIVNOSTI_NA_ZEMLE.html?page=0,1 (10.05.2011).
8. Комиссия по атмосферным наукам. Тринадцатая сессия ОСЛО, НОРВЕГИЯ, 12-20 февраля 2002г. КАН-XIII/PINK 8 (19.02.2002 г.). [Электронный ресурс]:
http://meteoinfo.ru/climate-WMO (16.05.2011).
9. Takens F. Detecting strange attractors in turbulence // Lec. NotesMath., 1981. V. 898. 366-381.
10. Орлов А.И. Статистические методы прогнозирования. Источник: Международная Академия исследований будущего (IFRA). Российское отделение – Академия прогнозирования. [Электронный ресурс]:
http://www.maib.ru/prognostication/methodsandmodels/methodsandmodels_45.html (14.05.2011).
11. Википедия: свободная энциклопедия. [Электронный ресурс]:
http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7 (14.05.2011).
12. Носов С.С., Беловодский В.Н. Предварительная обработка временных метеорядов: методы, эксперименты, результаты. Источник: Информационные управляющие системы и компьютерный мониторинг – 2011 / Материалы II всеукраинской научно-технической конференции студентов, аспирантов и молодых учёных. – Донецк, ДонНТУ – 2011, с. 119-123.
13. Сивяков А.С., Трофименко Е.С., Беловодский В.Н. Регрессионное уравнение Эглайса: метод, реализация, эксперимент. Источник: Компьютерный мониторинг и информационные технологии 2009 / Материалы V международной научной конференции студентов, аспирантов и молодых ученых. – Донецк, ДонНТУ – 2009. [Электронный ресурс]:
http://www.uran.donetsk.ua/~masters/2010/fknt/sivyakov/library/article4.htm (02.05.2011).
14. Климова Е.А. Разработка дифференциальной математической модели эволюции метеопараметров и решение задач прогноза на ее основе. – Донецк, ДонНТУ, 2011. [Электронный ресурс]:
http://www.masters.donntu.ru/2011/fknt/klimova/diss/index.htm (на момент выполнения автореферата материалы автора не индексируются, однако переданы в электронном виде).
Про автора
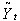 була функція від поточних не згладженого значення
була функція від поточних не згладженого значення  і попереднього згладженого
і попереднього згладженого  :
:
 ,
,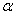 – параметр згладжування, причому
– параметр згладжування, причому 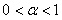 [12].
[12].

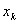 здійснюється пошук одного (найближчого) сусіда; збільшивши D на 1, визначають, які з сусідів виявилися хибними
(сильно розійшлися), а які - справжніми. Підраховують відношення числа помилкових сусідів до загальної кількості відновлених векторів.
Якщо при збільшенні D це число стає малим при деякому значенні D*, то останнє і є оцінкою розмірності простору,
в якому досягається вкладення траєкторії модельованого руху [6].
здійснюється пошук одного (найближчого) сусіда; збільшивши D на 1, визначають, які з сусідів виявилися хибними
(сильно розійшлися), а які - справжніми. Підраховують відношення числа помилкових сусідів до загальної кількості відновлених векторів.
Якщо при збільшенні D це число стає малим при деякому значенні D*, то останнє і є оцінкою розмірності простору,
в якому досягається вкладення траєкторії модельованого руху [6].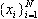 , утворений послідовністю N рівновіддалених значень деякої (можливо, випадкової) функції f(t):
, утворений послідовністю N рівновіддалених значень деякої (можливо, випадкової) функції f(t):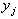 = X
= X є лінійним перетворенням вихідного процесу за допомогою дискретного оператора згортки, тобто:
є лінійним перетворенням вихідного процесу за допомогою дискретного оператора згортки, тобто:
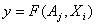 , де {
, де {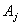 } – набір коефіцієнтів рівняння регресії, {
} – набір коефіцієнтів рівняння регресії, {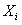 } – набір параметрів об'єкта [13].
} – набір параметрів об'єкта [13].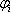 }. Вони задаються у вигляді:
}. Вони задаються у вигляді: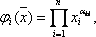
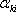 - різноманітні набори позитивних і негативних чисел. Причому
- різноманітні набори позитивних і негативних чисел. Причому
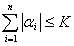 .
.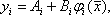 а також визначаються сумарні квадратичні відхилення:
а також визначаються сумарні квадратичні відхилення: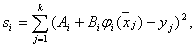
 . Потім обчислюється відповідне середньоквадратичне відхилення
. Потім обчислюється відповідне середньоквадратичне відхилення 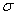 і виробляється побудова
і виробляється побудова 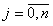 , {
, {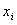 } – набір параметрів об'єкта,
} – набір параметрів об'єкта,
 , n – розмірність моделі, отримана на попередньому етапі. Ступінь полінома К спочатку роботи методу Еглайса задається користувачем, але, в кінцевому рахунку, визначається номером точки зламу на діаграмі елімінації, тобто при почерговому виключення з банку перспективних функцій.
, n – розмірність моделі, отримана на попередньому етапі. Ступінь полінома К спочатку роботи методу Еглайса задається користувачем, але, в кінцевому рахунку, визначається номером точки зламу на діаграмі елімінації, тобто при почерговому виключення з банку перспективних функцій.