RUS | UKR
| ENG
|| ДонНТУ
Портал магистров ДонНТУ

Носов Сергей Сергеевич
Факультет компьютерных наук и технологий
Специальность: Компьютерный эколого-экономический мониторинг
Научный руководитель: Беловодский Валерий Николаевич
Материалы по теме выпускной работы: Об авторе
| Библиотека
| Ссылки
| Отчет о поиске | |
Индивидуальный раздел
Реферат по теме выпускной работы
«Разработка конечной математической модели динамики метеопараметров и
прогнозирование их поведения на ее основе»
Актуальность темы
Одной из важных современных проблем человечества является достоверный прогноз погоды.
Нередко, прогноз погоды проводится с целью учета возможных негативных и катастрофических воздействий
на человеческую деятельность и обычно осуществляется с определенной долей достоверности.
Для хранения исходных данных наблюдаемых метеопоказателей необходимо создание одной большой или нескольких,
распределенных по территориальному или иному признаку, сравнительно меньших баз данных для сбора информации,
ее надлежащей обработке и осуществления прогноза. Как правило, это позволяет своевременно
реагировать на прогноз и принимать соответствующие меры.
Особенно заметный экономический эффект дает использование метеорологической информации в таких сферах деятельности,
как авиация, строительство, рыболовство, энергетика, судоходство, а также сельское хозяйство.
С научной точки зрения, предсказание погоды – одна из сложнейших задач физики атмосферы.
Совершенствование компьютерного оборудования позволяет реализовывать математические подходы и методы исследования атмосферы.
Каждый из них позволяет в той или иной степени прогнозировать метеоявления.
Таким образом, тема и результаты исследования в области прогнозирования
динамики метеопараметров обуславливаются решением задачи прогноза наблюдаемых метеопараметров.
Формулирование задач
Цель магистерской работы – разработать конечную математическую модель
динамики для прогнозирования метеопараметров в виде программного продукта, включающего в себя
ряд современных методов предварительной подготовки и составления прогнозов метеорологических данных.
Объектом исследования являются временные ряды наблюдаемых метеопараметров: температура, влажность, давление, скорость ветра.
Предметы исследования – методы предварительной подготовки и прогнозирования данных, качество и дальность результатов прогноза.
Гипотеза исследования – процесс составления прогноза будет проходить успешнее и продуктивнее при следующих условиях:
1. Использование современных методов при работе с временными рядами, таких как метод Эглайса [1],
метод главных компонент [2], экспоненциальное сглаживание [3], критерий Ирвина [3], линейная интерполяция [4];
2. Обзор существующих методов и подходов, используемых для прогноза метеопараметров:
выявление достоинств и недостатков; предложение собственной методики (математической модели);
3. Программная реализация, внедрение в практику предложенной математической модели.
Таким образом, задачами магистерской работы являются:
1. Изучить существующие методы предварительной подготовки и прогноза временных рядов,
и внедрить их в существующий прогностический комплекс;
2. Выполнить обзор существующих методов и походов прогнозирования;
3. Разработать математическую модель динамики метеопараметров;
4. Провести апробацию математической модели;
5. Реализовать программно предложенную модель;
6. Обеспечить информационную защиту программной математической модели.
Научная значимость работы
Исходя из цели проведения прогноза метеопоказателей, немаловажное значение имеет его достоверность,
которая, отчасти, определяется надежностью исходных данных, важной является задача предварительного анализа данных,
с целью исключения, по возможности, случайных помех или, наоборот, заполнения отсутствующих данных.
Научная значимость (новизна) работы появляется в двух случаях:
- решение старой задачи новыми методами;
- решение новой задачи старыми методами.
Научная значимость данной работы заключается в использовании новых подходов
к решению задачи прогнозирования динамики метеорядов, в частности использование:
- Интерполяционных методов на первом этапе работы, для первоначальной подготовки временного ряда;
- Методов определения наименьшей размерности модели, таких как метод ложных соседей и «Гусеница», что обеспечивает однозначность прогноза;
- Метода Эглайса для формирования прогностической модели.
Результаты реализации использованных в работе подходов планируется сравнить с результатами,
полученными при осуществлении прогноза с помощью прогностического комплекса.
Весомость перечисленных явлений на конечные результаты прогнозирования весьма существенна,
поэтому ниже на базе известных методов формулируются тезисы о практической ценности магистерской работы.
Предполагаемая практическая ценность результатов работы
Предполагаемая практическая ценность работы заключается в том, что получаемые результаты имеют практическую направленность.
В данной магистерской работе такой практической задачей является формирование прогноза.
Так, при проведении численных экспериментов по предварительной подготовке временного ряда, в зависимости от набора исходных данных,
относительная погрешность восстановления пропущенных значений составляет порядка 12%. Предварительная подготовка является первым этапом
предлагаемой конечной математической модели, и позволяет повысить точность прогноза вследствие
отсутствия аномальных значений и пробелов в данных временных метеорядов.
Разрабатываемые и предлагаемые методики обработки временных рядов,
предлагаемые способы прогнозирования направлены, в конечном счете, на повышение качества прогноза.
Практическая ценность заключается в решении задачи, имеющей практическую направленность, а именно: повышение точности прогноза.
Обзор исследований по теме в ДонНТУ
Построение математической модели динамики основано на обработке временных метеорядов,
полученных c метеостанции Vantage Pro 2, установленной на кафедре КСМ факультета КНТ ДонНТУ.
Данная метеостанция позволяет снимать данные по следующим метеорологическим показателям:
- Температура;
- Влажность;
- Давление;
- Скорость ветра.
На данный момент на кафедре КСМ уже разработан программный продукт, основой которого была
разработка методики краткосрочного прогноза наблюдаемых метеопоказателей по временным рядам метеопараметоров [5].
Он позволяет на основе рядов, снимаемых с метеостанции, осуществлять краткосрочное прогнозирование температуры, влажности, давления и скорости ветра.
Все данные по наблюдаемым метеопоказателям сохраняются на сервере кафедры КСМ
и аппаратно-программном комплексе экологического мониторинга атмосферного воздуха «АКИАМ».
Интервал замеров метеопараметров составляет 10 минут [6]. Таким образом, в процессе эксплуатации базы данных постоянно
формируется и постепенно накапливается совокупность временных рядов. Наличие этой информации делает вполне реальной задачу
разработки математической модели динамики временных рядов в рамках исследований в области осуществления прогноза погоды,
с использованием математических методов и сред разработки для программной реализации выполненной работы.
По теме магистерской работы в данной предметной области проводились исследования в ДонНТУ и в предыдущие года магистрами специальности КЭМ:
- Повзло Сергей Алексеевич «Разработка системы мониторинга метеопараметров атмосферы
с использованием инструментальных средств, работающих в реальном масштабе времени» (2006 год). Научный руководитель Аверин Геннадий Викторович;
- Иващенко Алеся Борисовна «Численный анализ математических моделей прогноза погоды» (2006 год).
Научный руководитель Беловодский Валерий Николаевич;
- Гриценко Анна Вячеславовна «Прогнозирование погодных условий по временным рядам метеовеличин» (2010 год).
Научный руководитель Беловодский Валерий Николаевич;
- Сивяков Артем Сергеевич «Построение прогностического комплекса и внедрение его в электронную сеть университета» (2011 год).
Научный руководитель Беловодский Валерий Николаевич.
Обзор предметной области исследований в мире
За последние десятилетия в мире используется ряд методов для прогноза погоды. Условно их можно разделить на следующие:
– синоптические методы – основаны на анализе погодных карт.
Сущность этих методов состоит в одновременном обзоре состояния атмосферы на обширной территории,
позволяющей определить характер развития атмосферных процессов и дальнейшее изменение погодных условий [7];
– численные методы – основаны на математическом решении систем полных уравнений
гидродинамики и получении прогностических полей давления, температуры на определенные промежутки времени.
Точность численных прогнозов зависит от скорости расчета вычислительных систем, от количества и качества информации, поступающей с метеостанций [7];
– анасамблевые походы – основаны на предположении о наличии неопределенности в сведениях о состоянии атмосферы.
Ансамблевое прогнозирование является численным методом прогнозирования, который используется для попытки создания репрезентативной выборки
из возможных будущих состояний динамической системы. Ансамблевое прогнозирование является одной из форм анализа Монте Карло: составляется
несколько численных прогнозов (с рядом незначительно отличающихся начальных условий), являющихся вполне правдоподобными,
учитывая набор прошлых и нынешних наблюдений или измерений. Если ансамбль хорошо построен, то его прогнозы охватят весь диапазон возможных результатов,
включая ряд образований, где могут возрастать неопределенности [8];
– методы нелинейной динамики. В рамках данных методов получен ряд фундаментальных теоретических результатов
и разработаны методики, обосновывающие принципиальную возможность прогнозирования физических процессов на базе их временных рядов.
Теоретическим фундаментом этих разработок и методов является теорема Такенса. Одной из его основополагающих идей является то,
что при построении эмпирических моделей по временному ряду в качестве недостающих переменных можно использовать или последовательные значения доступной
наблюдаемой величины, или ее последовательные производные. Было доказано, что при реконструкции по скалярной временной реализации динамической системы и
метод временных задержек, и метод последовательных производных гарантируют, что в новых переменных будет получено эквивалентное описание исходной
динамической системы при достаточно большой размерности восстановленных векторов D. А именно, должно выполняться условие D>2d, где d – размерность
множества M в фазовом пространстве исходной системы, на котором происходит моделируемое движение [9]. Эти утверждения составляют содержание теорем Такенса.
– статистический метод – предполагает прогнозирование погоды на основе некоторой статистики,
из которой формируется временной ряд, и производится реконструкция (восстановление) уравнений. Отличие от методов нелинейной динамики состоит в том,
что в качестве недостающих данных используются значения, вычисленные на основе уравнения, составленного на основе некоторой статистики наблюдаемой величины.
Простейшие методы восстановления, используемые для прогнозирования зависимости, исходят из заданного временного ряда, т.е. функции,
определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели.
Он может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Могут оказаться полезными предварительные преобразования переменных,
например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах. Метод наименьших модулей,
сплайны и другие методы экстраполяции применяются реже, хотя их статистические свойства зачастую лучше [10].
Для оценки точности прогноза используются вероятностно-статистические модели восстановления зависимости,
например, строят наилучший прогноз по методу максимального правдоподобия. Существуют параметрические (обычно на основе модели нормальных ошибок)
и непараметрические оценки точности прогноза и доверительные границы для прогноза (на основе Центральной Предельной Теоремы теории вероятностей).
Применяются также эвристические приемы, которые не основаны на вероятностно-статистической теории: метод скользящих средних,
метод экспоненциального сглаживания. Указанные методы не являются методами прогноза, однако могут использоваться для оценки его точности [11].
Содержание работы по этапам
Этап 1. Предварительная подготовка временного ряда.
1. Просмотр на наличие пустот и их заполнение (в случае обнаружения).
На данном этапе предварительной обработки пробелы в данных генерировались
в тренировочном временном ряду температуры псевдослучайным образом. Каждое значение временного ряда могло оказаться нулевым с некоторой вероятностью.
Таким образом, в исходном, тренировочном ряду образовывались пустоты различной длины. Устранение пустот осуществлялось различными методами,
в зависимости от длины образовавшихся пустот. Так, если длина пробелов в данных была единичной, и пробелы располагались не по краям ряда,
то пропущенные значения заменялись средним арифметическим их соседних значений. Иначе использовался метод линейной интерполяции, с некоторыми вариациями.
В зависимости от местоположения пробела в данных, использовалась линейная интерполяция «вперед», «назад», «нейтральная».
В расчетных соотношениях линейной интерполяции «нейтральной» для получения пропущенных значений использовались значения до и после пробелов в данных,
а также их индексы. Если использовалась линейная интерполяция «вперед», то в расчетных соотношениях использовались значения перед пробелом в данных
и их индексы. В случае применения линейной интерполяции «назад» производились аналогичные интерполяции «вперед» за исключением использования
в расчетных соотношениях значений, идущих после пробелов в данных. В зависимости от наличия пробелов на концах ряда, выполнялось комбинирование методов.
Полученные значения усреднялись, в зависимости от количества применявшихся методов.
2. Повторный просмотр, выявление и корректировка аномальных значений.
Выявление аномальных значений осуществлялось с использованием критерия Ирвина.
А их последующая корректировка осуществлялась методом линейной интерполяции (в случае аномалий, имеющих длину более единицы),
позволяющего заменить аномальные значения временного ряда значениями, соответствующими динамике ряда. Так, например,
если на определенном промежутке значения временного ряда возрастали, то имела место некоторая тенденция и значение,
на которое было заменено аномальное, соответствовало эволюции определенного промежутка ряда. В случае с убывающими значениями ряда
производились аналогичные операции. Аномальные значения временных рядов единичной длины заменялись средним арифметическим соседних значений.
3. Окончательный просмотр, сглаживание.
Использование метода экспоненциального сглаживания применительно к полученному, в результате выполнения второго этапа, временному ряду.
А именно к тем значениям, которые были получены в результате замены аномальных значений новыми. При сглаживании, значением текущего сглаженного значения
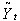 являлась функция от текущего не сглаженного значения
являлась функция от текущего не сглаженного значения  и предыдущего сглаженного
и предыдущего сглаженного  :
:
 ,
,
где 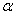 – параметр сглаживания, причем
– параметр сглаживания, причем 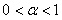 [12].
[12].
Выбор значения параметра сглаживания производился с помощью составленного
в среде разработки Visual Studio 2008 Professional программного обеспечения. Поиск наилучшего значения 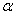 осуществлялся
в диапазоне
осуществлялся
в диапазоне 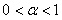 с шагом 0.0001: значение
с шагом 0.0001: значение 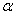 , при котором среднеквадратичное отклонение
было минимальным, считалось наилучшим. Выбранное значение принималось в качестве наилучшего и использовалось при дальнейших расчетах [12].
Результаты сглаживания оказались удовлетворительными, так как полученный временной ряд не содержал шумовых составляющих.
, при котором среднеквадратичное отклонение
было минимальным, считалось наилучшим. Выбранное значение принималось в качестве наилучшего и использовалось при дальнейших расчетах [12].
Результаты сглаживания оказались удовлетворительными, так как полученный временной ряд не содержал шумовых составляющих.
Исходный временной ряд считывался из файла и загружался в память программы:
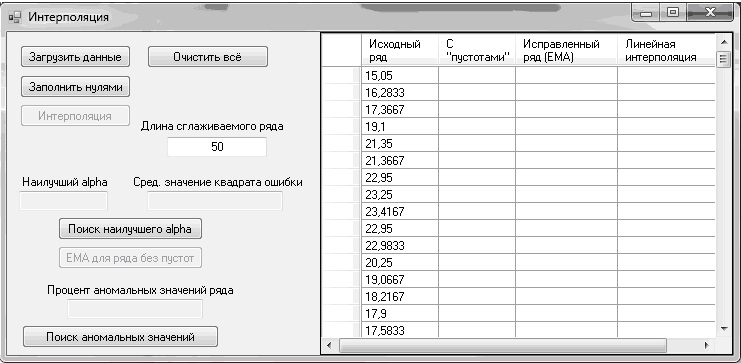
Рисунок 1 – Исходный временной ряд
Далее, выбиралось значение длины сглаживаемого ряда (например, 50),
исходные данные заполнялись пробелами (нажатием на соответствующие кнопки).
Был получен результат численного эксперимента по предварительной подготовке временного ряда, содержащий:
- результат поиска наилучшего значения параметра сглаживания;
- среднее значения квадрата ошибки;
- процент аномальных значений для 50 первых значений временного ряда [12]:

Рисунок 2 – Результат численного эксперимента
Результат выполнения этапа №1 – подвергнутый предварительной подготовке временной ряд.
Этап 2. Выбор размерности модели.
Для решения этой задачи используется различные методы оценки: ложных соседей, главных компонент, Грассбергера – Прокаччиа,
метод хорошо приспособленного базиса. Применяется метод ложных соседей для определения наименьшей размерности модели,
которая обеспечивает однозначность прогноза. Метод «Гусеница» является процедурой преобразования одномерного временного ряда в многомерный.
Метод ложных соседей основан на проверке того свойства, что фазовая траектория,
восстановленная в пространстве достаточной размерности не должна иметь самопересечений.
При пробной размерности D для каждого восстановленного вектора
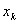 осуществляется поиск одного (самого близкого) соседа; увеличив D на 1, определяют, какие из соседей оказались ложными
(сильно разошлись), а какие – истинными. Подсчитывают отношение числа ложных соседей к общему числу восстановленных векторов.
Если при увеличении D это число становится малым при некотором значении D*, то последнее и есть оценка размерности пространства,
в котором достигается вложение траектории моделируемого движения [6].
осуществляется поиск одного (самого близкого) соседа; увеличив D на 1, определяют, какие из соседей оказались ложными
(сильно разошлись), а какие – истинными. Подсчитывают отношение числа ложных соседей к общему числу восстановленных векторов.
Если при увеличении D это число становится малым при некотором значении D*, то последнее и есть оценка размерности пространства,
в котором достигается вложение траектории моделируемого движения [6].
Существует ряд алгоритмов, являющихся реализацией метода «Гусеница».
Базовый алгоритм состоит из четырех последовательных этапов. При этом рассматривается временной ряд
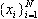 , образованный последовательностью N равноотстоящих значений некоторой (возможно, случайной) функции f(t):
, образованный последовательностью N равноотстоящих значений некоторой (возможно, случайной) функции f(t):
xi = f((i-1)*D*t),
где i = 1,2,…,N.
Рассмотрим более подробно каждый этап.
Шаг №1 (Развертка одномерного ряда в многомерный).
Выбирается некоторое число M < N, называемое длиной гусеницы, и представляются первые M значений последовательности f
в качестве первой строки матрицы X. В качестве второй строки матрицы берутся значения последовательности с x2 по xM+1.
Последней строкой с номером k = N – M + 1 будут последние M элементов последовательности.
В общем случае, выбор длины гусеницы М существенно зависит от задачи,
решаемой этим методом. Наиболее типичные и исследованные разработчиками случаи:
1. Если решается задача анализа исходного временного ряда, например, с целью отыскания скрытых периодичностей
с неизвестными периодами, то можно использовать значение длины гусеницы М, равное половине длины ряда N:
М = N / 2.
Если временной ряд длинный, то значение М выбирается такое, которое позволяет использовать компьютерные ресурсы;
2. Если решается более узкая задача, например, сглаживание исходного временного ряда или
выделение периодичности с известным периодом, то работает другой механизм, связанный с методом «Гусеница» – механизм фильтрации.
Следует отметить, что при выборе длины гусеницы М должно выполняться условие: M < N;
3. Если решается задача наилучшего выделения (или исключения) периодического, но
не обязательно гармонического, колебания с известной частотой и, следовательно, периода. В этом случае бывает необходимо для лучшего решения задачи
уменьшить длину временного ряда N. Периодические колебания наилучшим образом выделяются, если М и N кратны длине периода выделяемого колебания.
Далее, согласно данной схеме (за исключением стандартизации признаков), проводится анализ главных компонент (АГК).
Таким образом, выбранное значение M является начальным. Далее используется метод главных компонент для окончательного его определения.
Шаг №2. (Анализ главных компонент: сингулярное разложение выборочной ковариационной матрицы)
Сначала вычисляется матрица V = (1/k)XTX, где k = N – M + 1 – объём выборки. Несмотря на то,
что ее элементы не центрированы, далее матрица V называется ковариационной, иногда – нецентральной ковариационной.
Следующий шаг состоит в вычислении собственных чисел и собственных векторов матрицы V, т.е. разложение ее V = PLPT,
где L – диагональная матрица, на диагонали которой стоят упорядоченные по убыванию собственные числа, а P – ортогональная матрица собственных векторов матрицы V.
Матрицы L и P совместно имеют множество интерпретаций, основанных на АГК. В частности, матрицу P можно рассматривать как матрицу перехода к главным компонентам
XP = Y = (y1,y2,...,yM).
При выборе длины гусеницы, равной N – M + 1, собственные вектора и главные компоненты (с точностью до нормировки) меняются местами.
Шаг №3. (Отбор главных компонент)
В силу свойств матрицы P можно представить матрицу ряда X как X = Y PT. Таким образом, получается разложение
матрицы ряда по ортогональным составляющим (главным компонентам).
В то же время преобразование 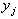 = X
= X является линейным преобразованием
исходного процесса с помощью дискретного оператора свертки, т.е.
является линейным преобразованием
исходного процесса с помощью дискретного оператора свертки, т.е.

Таким образом, процедура «Гусеница» порождает набор линейных фильтров, настроенных на составляющие исходного процесса.
При этом собственные векторы матрицы V выступают в роли переходных функций соответствующих фильтров.
Визуальное и аналитическое изучение, как собственных векторов, так и главных компонент,
полученных в результате линейной фильтрации, может дать информацию о структуре изучаемого процесса и свойствах составляющих его слагаемых.
В частности, среди главных компонент можно выделить:
1. относящиеся к тренду (медленно меняющиеся);
2. периодические;
3. шумовые.
Для нахождения периодических составляющих чрезвычайно большую визуальную информацию
дает изучение двумерных графиков, аналогичных фигурам Лиссажу, когда по осям x и y откладываются различные пары собственных векторов или главных компонент.
Шаг №4. (Восстановление одномерного ряда)
Следующим ключевым элементом метода «Гусеница» является процедура восстановления. Эта процедура основана
на разложении X = Y PT. Восстановление проводится по данному набору главным компонентам, если при
применении формулы восстановления X = Y* PT матрица Y* получена из матрицы Y обнулением всех не входящих в набор главных компонент.
Таким образом, можно получить интересующее нас приближение матрицы ряда или интерпретируемую часть этой матрицы.
Переход к исходному ряду формально может быть осуществлен усреднением матрицы ряда по побочным диагоналям и может привести к некоторому искажению полученной структуры.
При программной реализации этапы приведенного выше алгоритма не воспроизводятся непосредственно.
Например, этап построения матрицы X отсутствует, а формулы преобразованы к виду, удобному для проведения ускоренных вычислений.
Основным управляющим параметром метода является M – длина гусеницы.
При геометрической интерпретации этот параметр является размерностью пространства, в котором исследуется траектория многомерной ломаной линии,
в которую переводится исходный временной ряд методом «гусеница». Максимальным значением М является M <= N / 2,
так как размерность множества k точек (вершин ломаной) в M - мерном пространстве не превосходит min(M,k-1).
Этот подход тесно связан с аналитической интерпретацией метода гусеница как аппроксимацией решения уравнения в конечных разностях с l коэффициентами.
Можно сказать, что l – это число степеней свободы функции f(t), а следовательно, и соответствующего ей временного ряда.
В методе «Гусеница» это выразится в том, что при M > l у ковариационной матрицы окажется только l ненулевых собственных чисел
(учитывая ограниченную точность вычислений, остальные M-l будут почти нулевые). Однако, в реальных исследованиях, эта ситуация достаточно редкая.
Результат выполнения этапа №2 – целочисленное значение – размерность модели,
которая должна быть меньше, чем длина временного ряда (согласно методу «Гусеница»).
Этап 3. Формирование прогностических моделей.
На данном этапе работы производится формирование прогностических моделей, с
использованием метода Эглайса (для получения оператора эволюции), целесообразность использования которого состоит в необходимости синтеза уравнения регрессии.
Данный метод заключается в следующем. Пусть имеется информация об объекте, заданная в виде таблицы,
где каждой точке в пространстве параметров соответствует определенный отклик. Требуется синтезировать соответствующее уравнение регрессии в виде
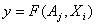 , где {
, где {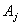 } – набор коэффициентов уравнения регрессии, {
} – набор коэффициентов уравнения регрессии, {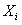 } – набор параметров объекта [13].
} – набор параметров объекта [13].
Алгоритм формирования регрессионного уравнения разбивается на следующие этапы:
1. формирование банка элементарных функций {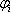 }. Они задаются в виде:
}. Они задаются в виде:
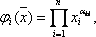
где n – число параметров объекта, 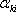 - всевозможные наборы положительных и отрицательных чисел.
Причем
- всевозможные наборы положительных и отрицательных чисел.
Причем 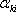 ограничено следующим условием:
ограничено следующим условием:
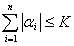 .
.
Предполагается, что K задаётся пользователем. Каждая функция представляется в виде массива степеней их аргументов.
2. отбор банка перспективных, в некотором смысле, функций.
На этом этапе, с использованием метода наименьших квадратов, осуществляется отбор функций, дающих минимальное отклонение.
3. поочередное исключение (элиминация) отобранных функций и синтез регрессионного уравнения.
Смысл последнего этапа заключается в следующем. Можно полагать, что среди отобранных функций
только часть необходима в синтезируемом уравнении регрессии. Остальные из банка отобранных функций необходимо исключить.
Пусть отобрано, например, всего p перспективных функций. Тогда имеется p вариантов исключения одной функции из состава перспективных.
Для всех функций банка по методу наименьших квадратов вычисляются коэффициенты элементарных уравнений регрессии в виде
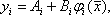 а также определяются суммарные квадратичные отклонения:
а также определяются суммарные квадратичные отклонения:
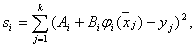
где  . Затем вычисляется соответствующее среднеквадратичное отклонение
. Затем вычисляется соответствующее среднеквадратичное отклонение 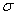 и производится построение
и производится построение 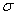 (i) на диаграмме элиминации. Пока из уравнения регрессии исключаются несущественные функции,
(i) на диаграмме элиминации. Пока из уравнения регрессии исключаются несущественные функции,
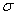 меняется мало. Когда же остаются существенные функции, то исключение любой из них заметно увеличивает среднеквадратичное отклонение
меняется мало. Когда же остаются существенные функции, то исключение любой из них заметно увеличивает среднеквадратичное отклонение 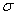 .
Поэтому, излом на диаграмме элиминации свидетельствует о получении наиболее предпочтительного уравнения регрессии [13].
.
Поэтому, излом на диаграмме элиминации свидетельствует о получении наиболее предпочтительного уравнения регрессии [13].
Таким образом, уравнение регрессии, синтезированное при помощи метода Эглайса, представляется алгебраическим многочленом (полиномом):
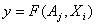 ,
,
где {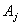 } – набор коэффициентов уравнения регрессии,
} – набор коэффициентов уравнения регрессии, 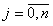 , {
, {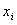 } – набор параметров объекта,
} – набор параметров объекта,
 , n – размерность модели, полученная на предыдущем этапе. Степень полинома К вначале работы метода Эглайса задаётся пользователем,
но, в конечном итоге, определяется номером точки излома на диаграмме элиминации, то есть при поочередном исключении из банка перспективных функций.
, n – размерность модели, полученная на предыдущем этапе. Степень полинома К вначале работы метода Эглайса задаётся пользователем,
но, в конечном итоге, определяется номером точки излома на диаграмме элиминации, то есть при поочередном исключении из банка перспективных функций.
Результат выполнения этапа №3 – оператор эволюции (динамики) временных рядов – регрессионное уравнение,
ограниченное размерностью модели, полученной на предыдущем этапе.
Этап 4. Проведение экспериментов
1. Подгонка модели.
Прогнозируется динамика временного метеоряда: значения рассчитываются на основе полученного в пункте 2 этапа 3 оператора эволюции.
2. Диагностическая проверка модели.
Производится сравнение полученных прогнозных значений с соответствующими исходными значениями
временного ряда наблюдаемого метеопараметра путем расчета относительной погрешности (ошибка, в процентах) полученного результата.
Так, было проведено 48 экспериментов [14] на разработанном прогностическом комплексе (в качестве прогнозируемого метеопараметра служила температура),
с использованием следующих методов:
а) метод главных компонент:
Проведено 24 эксперимента. Наилучшие результаты прогноза на:
- 1 час: линейная – 2, нелинейная – 4, регрессионная – 0
- 3 часа: линейная – 2, нелинейная – 0, регрессионная – 4
- 6 часов: линейная – 2, нелинейная – 3, регрессионная – 1
- 9 часов: линейная – 2 , нелинейная – 2, регрессионная – 2
Итог: линейная – 8, нелинейная – 9, регрессионная – 7 [14].
При осуществлении прогноза с заблаговременностью в 1 и 6 часов, нелинейная нейронная сеть является наилучшей.
Регрессионная нейронная сеть является наиболее предпочтительной при осуществлении прогноза с заблаговременностью 3 часа;
б) метод ложных соседей:
Проведено 24 эксперимента. Наилучшие результаты прогноза на:
- 1 час: линейная – 3, нелинейная – 1, регрессионная – 2
- 3 часа: линейная – 1, нелинейная – 2, регрессионная – 3
- 6 часов: линейная – 4, нелинейная – 0, регрессионная – 2
- 9 часов: линейная – 3, нелинейная – 1, регрессионная – 2
Итог: линейная – 11 , нелинейная – 4, регрессионная – 9 [14].
При осуществлении прогноза с заблаговременностью в 1, 6 и 9 часов, линейная нейронная сеть является наилучшей, опережая по точности регрессионную сеть.
Общий итог (48 экспериментов). Наилучшие результаты:
Линейная – 19 из 48 – 39,58%
Нелинейная – 13 из 48 – 27,01%
Регрессионная – 16 из 48 – 33,3%
Таким образом, наилучшей нейронной сетью является линейная, так как в большинстве случаев она обеспечивает наибольшую точность прогноза температуры.
3. Пригодность модели.
На основании предыдущего (пункт 2 этапа 4) пункта делается вывод о пригодности модели для прогноза значений.
Определяется среднее значение квадрата ошибки расчетов, а также минимум и максимум. Если погрешность лежит в допустимых пределах,
то производится переход к пункту 4 этапа 4, иначе – переход ко второму этапу.
4. Использование модели.
Осуществляется прогноз динамики временного ряда наблюдаемого метеопараметра (согласно рассчитанному оператору эволюции)
с заранее заданной заблаговременностью (количество временных промежутков, на которые осуществляется прогноз).
Суть данного шага этапа состоит в следующем.
4.1. С помощью разработанного прогностического комплекса выбирается наилучшая нейронная сеть;
4.2. Разрабатывается программное обеспечение, реализующие прогнозирование метеопоказателей
с заданной заблаговременностью, с использованием выбранной нейронной сети и метода Эглайса;
4.3. Проводятся вычислительные эксперименты для различных сезонных промежутков времени (лето, осень и т.д.);
4.4. Сравниваются результаты;
4.5. Формулируются выводы.
В общем виде, предполагаемые этапы работы можно представить следующим образом:
 Рисунок 3 - Схема работы разработанной математической модели
Рисунок 3 - Схема работы разработанной математической модели
(анимация: объём - 171 КБ, размер - 313х452; количество кадров - 14;
бесконечное число циклов повторения; задержка между кадрами - 30 мс; задержка между последним и первым кадром - 150 мс)
Этап 5. Программная реализация.
Разработка программного обеспечения, реализующего разработанную конечную математическую модель динамики метеопараметров
в виде дополнительного функционала к разработанному прогностическому комплексу, с целью увеличения достоверности прогноза.
Проведение серии вычислительных экспериментов для сравнения разработанной модели с моделями, присутствующими в прогностическом комплексе.
Апробация
Результаты первого этапа работы докладывались на II всеукраинской научно-технической конференции студентов,
аспирантов и молодых ученных «Информационные управляющие системы и компьютерный мониторинг» 12-14 апреля 2011г.
и опубликованы в соответствующем сборнике (с. 119-123) [12].
Выводы
В качестве основной задачи разработки конечной математической модели динамики метеопараметров
была принята задача дополнения и усовершенствования разработанного прогностического комплекса, а также адаптация
разработанной модели для лабораторных исследований. В результате работы был проведен анализ литературы по методам
предварительной подготовки и прогнозирования временных рядов. Был программно реализован первый этап работы математической модели,
а также проведен ряд вычислительных экспериментов по предварительной подготовке временных рядов для дальнейшей работы с ними.
Результаты работы докладывались на II международной конференции студентов, аспирантов и молодых ученых (материалы: том 1, с.119-123) [12].
Предлагаемая модель имеет возможность прогнозирования метеопараметров, с помощью методов реконструкции модельных уравнений,
основанных на анализе временных рядов, для осуществления численного прогноза погоды с целью повышения качества и заблаговременности прогноза.
При написании данного автореферата магистерская работа еще не завершена. Срок окончательной готовности работы – декабрь 2011 года.
Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список литературы
1. Эглайс В.О. Аппроксимация табличных данных многомерным уравнением регрессии. –
Вопросы динамики и прочности: Рига, 1981, Вып. 39. – с.120-125.
2. Википедия: свободная энциклопедия. [Электронный ресурс]:
http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D1%8B%D1%85%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82 (15.05.2011).
3. Татаренко С.И. Методы и модели анализа временных рядов: Метод. указания к лабораторным работам. Тамбов: Тамбовский государственный технический университет, 2008. – 19с.
4. Википедия: свободная энциклопедия. [Электронный ресурс]:
http://ru.wikipedia.org/wiki/Линейная_интерполяция (15.05.2011).
5. Гриценко А.В. Реконструкция уравнений и прогнозирование метеопараметров по их временным рядам. – Донецк, ДонНТУ, 2010. – 149с.
6. Сивяков А.С. Построение прогностического комплекса и внедрение его в электронную сеть университета. – Донецк, ДонНТУ, 2010. [Электронный ресурс]:
http://www.masters.donntu.ru/2010/fknt/sivyakov/diss/index.htm (28.04.2011).
7. Онлайн Энциклопедия Кругосвет ПРОЯВЛЕНИЯ СОЛНЕЧНОЙ АКТИВНОСТИ НА ЗЕМЛЕ. [Электронный ресурс]:
http://www.krugosvet.ru/enc/nauka_i_tehnika/astronomiya/PROYAVLENIYA_SOLNECHNO_AKTIVNOSTI_NA_ZEMLE.html?page=0,1 (10.05.2011).
8. Комиссия по атмосферным наукам. Тринадцатая сессия ОСЛО, НОРВЕГИЯ, 12-20 февраля 2002г. КАН-XIII/PINK 8 (19.02.2002 г.). [Электронный ресурс]:
http://meteoinfo.ru/climate-WMO (16.05.2011).
9. Takens F. Detecting strange attractors in turbulence // Lec. NotesMath., 1981. V. 898. 366-381.
10. Орлов А.И. Статистические методы прогнозирования. Источник: Международная Академия исследований будущего (IFRA). Российское отделение – Академия прогнозирования. [Электронный ресурс]:
http://www.maib.ru/prognostication/methodsandmodels/methodsandmodels_45.html (14.05.2011).
11. Википедия: свободная энциклопедия. [Электронный ресурс]:
http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7 (14.05.2011).
12. Носов С.С., Беловодский В.Н. Предварительная обработка временных метеорядов: методы, эксперименты, результаты. Источник: Информационные управляющие системы и компьютерный мониторинг – 2011 / Материалы II всеукраинской научно-технической конференции студентов, аспирантов и молодых учёных. – Донецк, ДонНТУ – 2011, с. 119-123.
13. Сивяков А.С., Трофименко Е.С., Беловодский В.Н. Регрессионное уравнение Эглайса: метод, реализация, эксперимент. Источник: Компьютерный мониторинг и информационные технологии 2009 / Материалы V международной научной конференции студентов, аспирантов и молодых ученых. – Донецк, ДонНТУ – 2009. [Электронный ресурс]:
http://www.uran.donetsk.ua/~masters/2010/fknt/sivyakov/library/article4.htm (02.05.2011).
14. Климова Е.А. Разработка дифференциальной математической модели эволюции метеопараметров и решение задач прогноза на ее основе. – Донецк, ДонНТУ, 2011. [Электронный ресурс]:
http://www.masters.donntu.ru/2011/fknt/klimova/diss/index.htm (на момент выполнения автореферата материалы автора не индексируются, однако переданы в электронном виде).
ДонНТУ
>
Портал магистров ДонНТУ ||
Об авторе | Библиотека
| Ссылки
| Отчет о поиске | |
Индивидуальный раздел
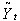 являлась функция от текущего не сглаженного значения
являлась функция от текущего не сглаженного значения  и предыдущего сглаженного
и предыдущего сглаженного  :
:
 ,
,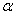 – параметр сглаживания, причем
– параметр сглаживания, причем 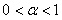 [12].
[12].

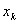 осуществляется поиск одного (самого близкого) соседа; увеличив D на 1, определяют, какие из соседей оказались ложными
(сильно разошлись), а какие – истинными. Подсчитывают отношение числа ложных соседей к общему числу восстановленных векторов.
Если при увеличении D это число становится малым при некотором значении D*, то последнее и есть оценка размерности пространства,
в котором достигается вложение траектории моделируемого движения [6].
осуществляется поиск одного (самого близкого) соседа; увеличив D на 1, определяют, какие из соседей оказались ложными
(сильно разошлись), а какие – истинными. Подсчитывают отношение числа ложных соседей к общему числу восстановленных векторов.
Если при увеличении D это число становится малым при некотором значении D*, то последнее и есть оценка размерности пространства,
в котором достигается вложение траектории моделируемого движения [6].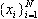 , образованный последовательностью N равноотстоящих значений некоторой (возможно, случайной) функции f(t):
, образованный последовательностью N равноотстоящих значений некоторой (возможно, случайной) функции f(t):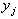 = X
= X является линейным преобразованием
исходного процесса с помощью дискретного оператора свертки, т.е.
является линейным преобразованием
исходного процесса с помощью дискретного оператора свертки, т.е.
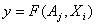 , где {
, где {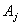 } – набор коэффициентов уравнения регрессии, {
} – набор коэффициентов уравнения регрессии, {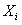 } – набор параметров объекта [13].
} – набор параметров объекта [13].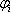 }. Они задаются в виде:
}. Они задаются в виде: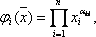
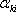 - всевозможные наборы положительных и отрицательных чисел.
Причем
- всевозможные наборы положительных и отрицательных чисел.
Причем 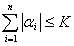 .
.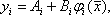 а также определяются суммарные квадратичные отклонения:
а также определяются суммарные квадратичные отклонения: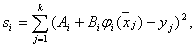
 . Затем вычисляется соответствующее среднеквадратичное отклонение
. Затем вычисляется соответствующее среднеквадратичное отклонение 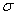 и производится построение
и производится построение 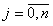 , {
, {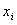 } – набор параметров объекта,
} – набор параметров объекта,
 , n – размерность модели, полученная на предыдущем этапе. Степень полинома К вначале работы метода Эглайса задаётся пользователем,
но, в конечном итоге, определяется номером точки излома на диаграмме элиминации, то есть при поочередном исключении из банка перспективных функций.
, n – размерность модели, полученная на предыдущем этапе. Степень полинома К вначале работы метода Эглайса задаётся пользователем,
но, в конечном итоге, определяется номером точки излома на диаграмме элиминации, то есть при поочередном исключении из банка перспективных функций.