Источник: Информационные управляющие системы и компьютерный мониторинг — 2011 / Материалы II всеукраинской научно-технической конференции студентов, аспирантов и молодых учёных. - Донецк, ДонНТУ - 2011, с. 119-123.
Введение
Во многих сферах деятельности человека важным моментом является прогнозирование событий.
В настоящее время, с ростом вычислительных возможностей техники, число методов и математических моделей обработки и прогноза увеличивается.
Все существующие методы условно можно разделить на фактографические и экспертные. Фактографические методы основаны на анализе информации об объекте,
а экспертные – на суждениях экспертов, которые получены при проведении коллективных или индивидуальных опросов. Каждая группа имеет достоинства, недостатки и
свою область применения. В статье рассматриваются фактографические методы.
Прогнозирование метеопараметров основано на идее экстраполяции. Под экстраполяцией обычно понимают распространение закономерностей, связей и соотношений, действующих в рассматриваемом периоде. Или, в более широком смысле, ее рассматривают как получение представлений о будущем на основе информации, относящейся к прошлому и настоящему. В процессе построения прогнозных моделей в их структуру иногда закладываются элементы будущего предполагаемого состояния метеопараметра, но в целом эти модели отражают закономерности, наблюдаемые в прошлом и настоящем. То есть прогноз возможен лишь относительно таких значений, которые в значительной степени детерминируются прошлым и настоящим.
Постановка задачи
Нередко, прогноз погоды проводится для учета возможных негативных и катастрофических воздействий на человеческую деятельность и обычно осуществляется
с определенной долей достоверности (вероятностью осуществления прогноза). В немалой степени, точность прогноза определяется надежностью исходных данных,
поэтому важной является задача предварительного их анализа, с целью исключения, по возможности, случайных помех или, наоборот, заполнения отсутствующих данных.
К числу характерных отрицательных моментов, которые желательно было бы учесть и устранить на этапе предварительного анализа,
можно отнести исключение случайных составляющих типа:
- пробелы – отсутствующие в базе данных значения измеряемого показателя (так называемые пустоты). Они могут возникать вследствие сбоя в канале передаче данных, или при неисправности датчиков измеряемых метеопоказателей, вследствие различного рода недоработок программного обеспечения, или сбоях в базах данных. Такие ошибки называются ошибками первого рода.
- аномальные значения – значения, которые не отвечают природе исследуемого временного ряда метеопоказателя и оказывающие существенное влияние на снижение точности и уменьшение заблаговременности (дальности) прогноза. Причинами появления аномальных значений могут быть технические ошибки при сборе, обработке и передаче информации, их можно постараться выявить и устранить, путем установки некоторых ограничений на значения конкретного метеопоказателя или принять меры к их недопущению (комбинирование методов обработки). Кроме того, аномальные значения могут возникать из-за воздействия факторов, имеющих объективный характер, но действующих эпизодически. Такие ошибки называются ошибками второго рода. Их невозможно устранить. Они исключаются из рассмотрения путем замены аномального значения ряда на среднее арифметическое двух соседних значений.
Весомость перечисленных явлений на конечные результаты прогнозирования весьма существенна, поэтому ниже на базе известных методов формулируются предложения, направленные на корректировку и реконструкцию исходных временных рядов, которые реализуются программно и проверяются экспериментально.
Рассматриваемые методы
При предварительной обработке временных рядов основное внимание уделяется выявлению и корректировке аномальных значений и осуществлении процедуры сглаживания ряда. Наиболее распространенными фактографическими методами предварительной обработки временных рядов являются:
1) определение наличия динамики и сезонных колебаний в данных;
2) определение смещения в данных;
3) предварительная фильтрация (частотные фильтры);
4) выявление и корректировка аномальных значений и заполнение пробелов в данных.
Так, определение наличия динамики представляет собой процедуру поиска во временном ряду последовательности наблюдений одного признака, в зависимости от последовательно возрастающих или убывающих значений другого признака. В таком случае, можно говорить о ряде динамики. Определение сезонных колебаний представляет собой частный случай определения динамики, подразумевающий определение динамики для сезонов года, сменяющих друг друга и повторяющихся.
Определение смещения в данных позволяет выявить закономерности (смещения друг относительно друга), например, в сезонных данных по каждому году. Производится сравнение данных некоторого периода одного года с данными соответствующего периода другого года. Таким образом, определяется смещение одних данных относительно других. Это может использоваться, например, при сравнении усредненных показателей температуры за определенные периоды.
Частотные фильтры лишь производят снижение амплитудно-частотной характеристики (АЧХ) данных, так как, в основном, являются частотными фильтрами невысоких порядков и обеспечивают требуемые характеристики АЧХ (в частности, хорошее подавление частот из полосы подавления и пренебрежение гладкостью АЧХ на частотах полос пропускания и подавления).
Первые три метода из числа рассматриваемых не учитывают наличие проблем, приводящих к появлению случайных составляющих в исходных данных. Следовательно, при их использовании, точность прогноза метеопоказателя будет ниже, чем при использовании метода выявления и корректировки аномальных значений и заполнения пробелов в данных. Данный метод учитывает проблемы, как правило, связанные с наличием поступления сигналов неизвестной ранее природы (так называемые аномалии или аномальные значения измеряемых показателей), пробелов в данных и так далее. Каждая из проблем может возникать по тем или иным причинам, среди которых могут быть как объективные причины, так и субъективные. В результате наличия проблем, в исходных данных могут содержаться случайные составляющие, снижающие достоверность исходных данных. Вследствие этого, первые три метода включены в число рассматриваемых, но в работе не используются.
Для выявления аномальных значений временных рядов используется критерий Ирвина, согласно которому, во временном ряду аномальным считается значение Yt в том случае, если значение критерия Ирвина для данного значения превышает допустимое (таблица 1):
lambda(t) = |Y(t) - Y(t-1)| / ksi,
где lambda(t) - критерий Ирвина, Y(t-1) - значение, предшествующее Y(t), ksi - среднеквадратичное отклонение.
То есть, во временном ряду Y(t) - аномальное значение, если lambda(t) > lambda(доп). Допустимые значения lambda(доп) уменьшаются с ростом длины ряда n.
Таблица 1 – Допустимые значения критерия Ирвина
| n | 10 | 20 | 30 | 50 | 100 |
| lambda(доп) | 1.5 | 1.3 | 1.2 | 1.1 | 1.0 |
Следует отметить, что любое значение во временном ряду может быть случайной составляющей. Для выявления и корректировки таковых проводились вычислительные эксперименты.
Вычислительные эксперименты
При сравнительном анализе и выборе процедур предварительной обработки акцент делался на указанные проблемы. Использовались «тренировочные» временные ряды: из базы данных метеостанции ДонНТУ Vantage Pro 2 определенной длины. Были предложены некоторые процедуры для заполнения пустот, которые были реализованы программно и проверены экспериментально. Суть этих процедур заключается в следующем.
При разработке метода предварительной обработки временных рядов вычислительные эксперименты (на примере временного ряда температуры) проводились по следующей схеме:
1. Просмотр на наличие пустот и их заполнение (в случае обнаружения).
На данном этапе предварительной обработки пробелы в данных генерировались
в тренировочном временном ряду температуры псевдослучайным образом. Каждое значение временного ряда могло оказаться нулевым с некоторой вероятностью.
Таким образом, в исходном, тренировочном ряду образовывались пустоты различной длины. Устранение пустот осуществлялось различными методами,
в зависимости от длины образовавшихся пустот. Так, если длина пробелов в данных была, и пробелы располагались не по краям ряда, то пропущенные
значения заменялись средним арифметическим их соседних значений. Иначе использовался метод линейной интерполяции, с некоторыми вариациями.
В зависимости от местоположения пробела в данных, использовалась линейная интерполяция «вперед», «назад», «нейтральная». В расчетных соотношениях линейной интерполяции
«нейтральной» для получения пропущенных значений использовались значения до и после пробелов в данных, а также их индексы. Если использовалась линейная интерполяция «вперед»,
то в расчетных соотношениях использовались значения перед пробелом в данных и их индексы. В случае применения линейной интерполяции «назад» производились аналогичные
интерполяции «вперед» за исключением использования в расчетных соотношениях значений, идущих после пробелов в данных. В зависимости от наличия пробелов на концах ряда,
выполнялось комбинирование методов. Полученные значения усреднялись, в зависимости от количества применявшихся методов.
2. Повторный просмотр, выявление и корректировка аномальных значений.
Выявление аномальных значений осуществлялось с использованием критерия Ирвина. А их последующая корректировка осуществлялась методом линейной интерполяции (в случае аномалий, имеющих длину более единицы), позволяющего заменить аномальные значения временного ряда значениями, соответствующими динамике ряда. Так, например, если на определенном промежутке значения временного ряда возрастали, то имела место некоторая тенденция и значение, на которое было заменено аномальное, соответствовало эволюции определенного промежутка ряда. В случае с убывающими значениями ряда производились аналогичные операции. Аномальные значения временных рядов единичной длины заменялись средним арифметическим соседних значений.
3. Окончательный просмотр, сглаживание.
На данном этапе использовался метод экспоненциального сглаживания применительно к полученному, в результате выполнения второго этапа, временному ряду. А именно к тем значениям, которые были получены в результате замены аномальных значений новыми [5]. При сглаживании, значением текущей сглаженного значения Y'(t) являлась функция от текущего не сглаженного значения Y(t) и предыдущего сглаженного Y'(t-1):
Y'(t) = alpha * Y(t) + (1 - alpha) * Y'(t-1),
где alpha - параметр сглаживания, причем 0 < alpha < 1
Выбор значения параметра сглаживания производилось с помощью составленного в среде разработки Visual Studio 2008 Professional программного обеспечения. Поиск наилучшего значения alpha осуществлялся в диапазоне 0 < alpha < 1 с шагом 0.0001: значение alpha, при котором среднеквадратичное отклонение было минимальным, считалось наилучшим. Выбранное значение принималось в качестве наилучшего и использовалось при дальнейших расчетах.
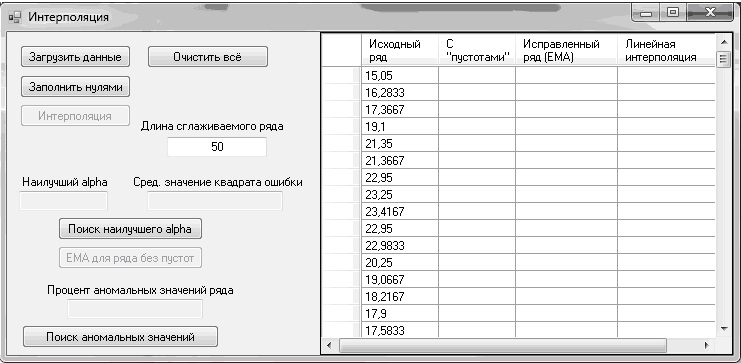
Исходный временной ряд считывался из файла и загружался в память программы:

Рисунок 1 – Исходный временной ряд
Далее, выбрав значение длины сглаживаемого ряда (например, 50), заполнив исходные данные пробелами, осуществив нажатия на соответствующие кнопки, был получен результат численного эксперимента, содержащий:
- результат поиска наилучшего значения параметра сглаживания;
- значение среднеквадратичного отклонения (среднего значения квадрата ошибки);
- процент аномальных значений в сглаживаемом ряду (50 первых значений):

Рисунок 2 – Результат численного эксперимента
Заключение
В работе предложен алгоритм, включающий в себя три последовательно выполняемые этапа. Произведены попытки учесть некоторые нюансы (для последующей корректной работы используемых методов обработки) в исходных временных рядах, такие как наличие:
- пустот в начале или в конце ряда;
- пустот с длиной более единицы;
- подряд идущих пустот, содержащих одно-два ненулевых значения.
Средняя относительная погрешность восстановления пропущенных значений, по результатам вычислительного эксперимента, составила (10 ± 2)%.