Автоматизированная система оптимального управления и координации деятельности сети предприятий, связанных взаимными поставками

Ситникова О.Д., Прокофьев А.В.
Кафедра ПМиИ ДонГТУ

Abstract

Sitnikova О., Prokoj'ev А. А computer-aided system of optimal management апd activity coordination of enterprises which linked bу supplies. Тhis work describes system оf optimal planning of industrial activity оf а corporation оr сопсеrn. Тhe planning directed tо realization оf а tеrminаl result (maxiтal profit) with тiniтal ехрепses оf таteriаl and financial resources. Тhis work includes description оf а mathematical model, used optimization methods, and а system structure.

Введение

В мировой практике известно множество форм организации хозяйственной деятельности – это различного рода синдикаты, корпорации, концерны, тресты. Они функционируют практически во всех сферах хозяйствования: в банковском деле, промышленности, транспорте, торговле и т. д. [1, 2, 5]

Наличие единого информационного пространства региона может способствовать внедрению передовых технологий в различных сферах, связанных с принятием обоснованных решений. Доступ к информационным источникам об экономической и производственной деятельности предприятий позволяет на основе глубокого анализа конъюнктуры рынка и объективных маркетинговых исследований успешно осуществлять организационную, посредническую и управленческую деятельность [3, 4].

В работе описывается разработанная авторами система оптимального планирования производственной деятельности .объединения предприятий типа корпорации или концерна, которое направлено на достижение конечного результата (максимальной прибыли) с минимальными затратами материальных и финансовых ресурсов. Система предназначена для поиска оптимальной схемы движения этих ресурсов между предприятиями-участниками объединения в соответствии с основными направлениями его деятельности в заданном временном периоде. В работе приведены: разработанная обобщенная математическая детерминированная модель задачи, используемые оптимизационные методы, структура программного комплекса.

1. Постановка задачи, математическая модель, методы

1. 1 Упрощенная модель

Имеется N предприятий, входящих в состав объединения. Продукция одних может являться сырьем для других. Продукция во всей схеме задается в одинаковых единицах (например, гривнах). Каждое предприятие можно представить в виде вершины с множеством входных дуг K_i, соответствующих возможным поставкам сырья, и множеством выходных дуг L_i, соответствующих возможным поставкам готовой продукции. Одно из предприятий является конечным получателем прибыли, пусть N-ое, тогда L_N=0.

Для каждой пары предприятий i и j известны:

U_ij и V_ij – нижняя и верхняя границы возможных поставок;

G_ij – коэффициенты изменения цены продукции или отношение цены продажи j к цене покупки i (с учетом всех дополнительных расходов), если G_ij >1, то дуга прибыльная.

Необходимо так организовать поставки, чтобы прибыль, полученная N-ым предприятием, была максимальной.

Неизвестные:

X_ij – объем поставки от i к j (на выходе из i).

Ограничения:

а) по дугам

U_ij ≤X_ij ≤V_ij, i,j=1..N;

б) по балансу предприятия (отдает на сумму полученного)

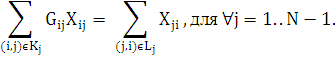
Функция цели:

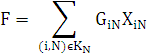
По модели это задача линейного программирования или в графовой интерпретации задача о максимальном циклическом потоке в сети с выигрышами [6]. Для ее решения построен эффективный полиноминальный алгоритм. Идея алгоритма заключается в следующем. От выигрышей дуг G_ij можно перейти к весам дуг G_ij= –log G_ij. Стираются циклы с оттоком в вершине N. Если вес такого цикла меньше нуля, он увеличивает функцию цели, по нему пропускается максимально возможный поток. Оптимальное решение найдено, когда ни для одной вершины не существует цикла отрицательного веса.

С помощью алгоритма решались задачи с сотнями предприятий и тысячами связей, время решения порядка нескольких секунд.

1.2 Обобщенная модель

Имеется N предприятий, входящих в состав объединения. Каждое выпускает K_j видов продукции. Продукция одних может являться сырьем для других. По каждому предприятию допускается наличие нижней и верхней границ на общий объем производимой продукции (если продукция измеряется в одинаковых единицах): d_i и h_i. По каждому виду продукции могут задаваться, исходя из возможностей предприятия, нижняя и верхняя границы отдаваемой р-ой продукции – а_i^p и b_i^p. Для каждого участника по каждому виду продукции указывается тип взаимоотношений с партнером по данной продукции. Возможны следующие варианты работы предприятия:

по схеме «ИЛИ» (например, на электростанцию уголь может поставляться с нескольких шахт в любом соотношении);

по схеме «И» (если требуется строгое соотношение видов сырья из заданного списка, например, для получения 1 т кокса по «давальческой схеме» необходимо 1.62 т концентрата + 20 грн. за оплату его доставки).

Если невозможно задать условия работы по одному из типов, то за счет введения фиктивных вершин можно представить любую смешанную схему.

Для каждой возможной дуги от участника i, поставляющего продукцию р, к участнику j, производящему продукцию q, задается следующая информация:

G_ij^pq – коэффициент пересчета количества товара р по дуге от i-гo предприятия к j-мy для продукции q, если на выходе i и на входе j продукция р измеряется в разных единицах, например, в тоннах и гривнах, иначе коэффициент изменения цены продукции р, т. е. отношение цены продажи по предприятию j для продукции q к цене покупки от предприятия i (с учетом налогов, таможенных выплат и других расходов), если равна 1, то без изменения, меньше 1 – с убытком по дуге, больше 1 – с прибылью;

R_ij^pq – коэффициент для давальческой схемы (тип «И»), если дуга (i,j) по продукции (р, q) является для j входной дугой давальческой схемы, показывает количество товара р, необходимого для получения единицы товара q, иначе R_ij^pq = О;

U_ij^pq , V_ij^pq – нижняя и верхняя границы количества товара по дуге (i,j) для продукции (р, q), выходящего из i, если границы не заданы, то U_ij^pq=0 , V_ij^pq= ∞ ;

M_ij^pq – доля продукции р в выходном потоке из предприятия 1, если это требование отсутствует, то M_ij^pq = 1;

S_ij^pq – количество товара р, поставленного в прошлом периоде от i к j под продукцию q и оставленного на предприятии j в единицах измерения для j;

Т_ij^pq – планируемый минимальный остаток продукции р, поставляемой от i к j под продукцию q, т. е. перепоставка, «оседает» на предприятии j в единицах измерения для j, если не планируется, то равна 0;

W_ij^pq – максимально возможная недопоставка продукции р от i к j под продукцию q в единицах измерения для j с перспективой в будущем рассчитаться с предприятием j за получаемую у него продукцию q, если долг на этом узле не планируется, то равна 0.

Среди множества предприятий условно выделено одно или несколько, являющихся конечными получателями прибыли, прибыль может получаться любыми или фиксированными видами продукции (деньги, векселя также рассматриваются как продукция). Необходимо рассчитать объемы поставок материалов и денежных ресурсов на некоторый период, с учетом планируемых остатков (создание резерва) и допустимых недопоставок по известным видам продукции на предприятиях с целью максимизации общей прибыли объединением (конечными получателями).

Неизвестные:

Х_ij^pq – количество продукции р, поставляемое от i к j под продукцию q (количество товара в единицах измерения выхода из i);

Y_ij^pq – количество продукции р, осевшей в j под продукцию q и пришедшей от i в единицах измерения j (перепоставка);

Y_ij^*pq – количество продукции р, недопоставленной j под продукцию q и пришедшей от i в единицах измерения j, остается как долг предприятия i перед j.

Заметим, что для конечных получателей в обозначениях исходных данных и неизвестных индекс q отсутствует.

Ограничения:

а) по переменным

Х_ij^pq ≥ 0, Y_ij^pq ≥ 0, Y_ij^*pq ≥ 0 для ∀ i,j=1..N, p=1..K_i, q= 1..K_j;

б) по поставке по дуге (i, j) по продукции (р, q)

U_ij ≤X_ij ≤V_ij для i,j=1..N, p=1..K_i, q= 1..K_j;

в) по планируемым остаткам

Y_ij^pq ≥ T_ij^pq для i,j=1..N, p=1..K_i, q= 1..K_j;

г) по планируемым недопоставкам

Y_ij^*pq ≤ W_ij^pq для i,j=1..N, p=1..K_i, q= 1..K_j;

д) по балансу предприятия

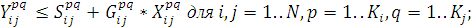
е) по возможностям поставщиков по каждому виду продукции

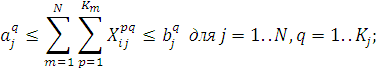
ж) по суммарным возможностям поставщиков

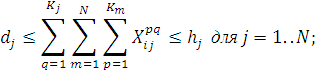
з) по вершинам схем типа «ИЛИ»

для j=1..N, q= 1..K_j;

и) по вершинам схем типа «И»

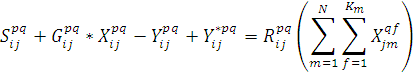
для i=1..N, j=1..N, p= 1..K_i, q= 1..K_j;

к) по доле продукция в выходном потоке предприятия

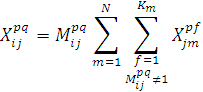
Функция цели:

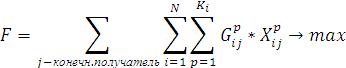
По модели это задача линейного программирования. Для ее решения на языке С++ реализован алгоритм, использующий модифицированный симплекс-метод с двусторонними ограничениями на неизвестные.

2. Структура автоматизированной системы

Программно система состоит из двух частей: оболочка и ядро системы,

Оболочка системы включает:

• интерфейс пользователя;
• блок ввода и редактирования исходных данных;
• блок формирования массивов информации;
• блок расшифровки оптимального решения;
• блок формирования выходных документов;
• блок поддержки сервисных функций.

Ядро системы включает:

• блок формирования уравнений, ограничений и функции цели;
• блок решения оптимизационной задачи.

Первая версия оболочки была реализована на языке Clipper, усовершенствованная – в среде Мiсrоsоft Ассеsа 97. Система успешно применялась для расчетов поставок по нескольким регионам Украины и России.

Литература

1. Мильнер Б. Крупные корпорации – основа подъема и ускоренного развития экономики. –Вопросы экономики, 1998, № 9, С. 67-72.
2. Мартынов Г. В. Многоотраслевые комплексы: проблемы и методы оптимизации. – М.: Наука, 1986. – 138 с.
3. Ларионов А. И. Экономико-математические методы в планировании. – М.: Высшая школа, 1991. – 122 с.
4. Михалевич В. С. Оптимизационные задачи производственно-транспортного планирования: модели, методы, алгоритмы. – М.: Наука, 1986. – 210 с.
5. Уманцив Г., Уманцив Ю., Лысенко О. Холдинговые компании в Украине. – Бизнесинформ, 1997, № 10, с. 12-17.
6. Липский В. Комбинаторика для программистов. – М.: Мир, 1988. – 213 с.

Вернуться к библиотеке