Распознавание образов и анализ сцен
В последние годы распознавание образов находит все большее применение в повседневной жизни. Распознавание речи и рукописного текста значительно упрощает взаимодействие человека с компьютером, распознавание печатного текста используется для перевода документов в электронную форму. Популярно мнение, что распознавание, как и прочие алгоритмы искусственного интеллекта, есть черная магия, недоступная простым смертным. На самом же деле алгоритмы, лежащие в основе распознавания, довольно очевидны, нужно лишь зайти чуть издалека и определиться с терминами.
Базовым является неопределимое понятие множества. В компьютере множество представляется набором неповторяющихся однотипных элементов. Слово "неповторяющихся" означает, что какой-то элемент в множестве либо есть, либо его там нет. Универсальное множество включает все возможные для решаемой задачи элементы, пустое не содержит ни одного.
В классической постановке задачи распознавания универсальное множество разбивается на части-образы. Образ какого-либо объекта задается набором его частных проявлений. В случае с распознаванием текста в универсальное множество войдут все возможные знаки, в образ "Ы" - все возможные начертания этой буквы, а программа распознавания занимается тем, что на основе небольшого набора примеров начертаний каждой буквы (обучающей выборки) определяет, какую из них символизирует введенная закорючка.
Методика отнесения элемента к какому-либо образу называется решающим правилом. Еще одно важное понятие - метрика, способ определения расстояния между элементами универсального множества. Чем меньше это расстояние, тем более похожими являются символы, звуки - то, что мы распознаем. Обычно элементы задаются в виде набора чисел, а метрика - в виде функции. От выбора представления образов и реализации метрики зависит эффективность программы, один алгоритм распознавания с разными метриками будет ошибаться с разной частотой (право на ошибку для программ распознавания так же характерно, как и для людей).
Хорошо показывает принцип работы распознавания образов элементарный алгоритм на основе метода множества эталонов. На входе его имеется обучающая выборка - набор примеров A'ij для каждого образа Ai, метрика d и сам распознаваемый объект x. С помощью метрики вычисляем расстояние от x до каждого элемента обучающей выборки d(x, aij) и находим условное расстояние d(x, Ai) как расстояние от x до ближайшего элемента из Ai. Элемент x относится к образу, который окажется ближе всех.
Практически тут требуется найти минимум расстояния по каждому классу и еще раз взять минимум. Любители трогать руками могут взять в качестве представления элемента пару координат, в качестве метрики - расстояние по теореме Пифагора, и набросать программку, которая будет выполнять описанную операцию над массивом точек двухмерного пространства и отображать это в графике.
Еще один элементарный алгоритм - метод k-ближайших соседей. Как следует из названия, в нем вводится дополнительный входной параметр, целое число k. Тут все еще проще - берется k ближайших к x элементов обучающей выборки и подсчитывается, сколько из них принадлежит к какому образу. К какому образу принадлежит больше, к тому относится и x.
В обоих алгоритмах может возникнуть неопределенная ситуация - когда x будет находиться на одинаковом расстоянии от нескольких образов. В таком случае программа должна либо спросить у пользователя, к какому образу относить элемент, либо тихо бросить жребий. Это зависит от требований к точности с одной стороны, и удобству использования с другой, лучше всего реализовать оба варианта.
Системы распознавания образов
Понятие образа
Образ, класс — классификационная группировка в системе классификации, объединяющая (выделяющая) определенную группу объектов по некоторому признаку.
Образное восприятие мира — одно из загадочных свойств живого мозга, позволяющее разобраться в бесконечном потоке воспринимаемой информации и сохранять ориентацию в океане разрозненных данных о внешнем мире. Воспринимая внешний мир, мы всегда производим классификацию воспринимаемых ощущений, т. е. разбиваем их на группы похожих, но не тождественных явлений. Например, несмотря на существенное различие, к одной группе относятся все буквы А, написанные различными почерками, или все звуки, соответствующие одной и той же ноте, взятой в любой октаве и на любом инструменте, а оператор, управляющий техническим объектом, на целое множество состояний объекта реагирует одной и той же реакцией. Характерно, что для составления понятия о группе восприятий определенного класса достаточно ознакомиться с незначительным количеством ее представителей. Ребенку можно показать всего один раз какую-либо букву, чтобы он смог найти эту букву в тексте, написанном различными шрифтами, или узнать ее, даже если она написана в умышленно искаженном виде. Это свойство мозга позволяет сформулировать такое понятие, как образ.
Образы обладают характерным свойством, проявляющимся в том, что ознакомление с конечным числом явлений из одного и того же множества дает возможность узнавать сколь угодно большое число его представителей. Примерами образов могут быть: река, море, жидкость, музыка Чайковского, стихи Маяковского и т. д. В качестве образа можно рассматривать и некоторую совокупность состояний объекта управления, причем вся эта совокупность состояний характеризуется тем, что для достижения заданной цели требуется одинаковое воздействие на объект. Образы обладают характерными объективными свойствами в том смысле, что разные люди, обучающиеся на различном материале наблюдений, большей частью одинаково и независимо друг от друга классифицируют одни и те же объекты. Именно эта объективность образов позволяет людям всего мира понимать друг друга.
Способность восприятия внешнего мира в форме образов позволяет с определенной достоверностью узнавать бесконечное число объектов на основании ознакомления с конечным их числом, а объективный характер основного свойства образов позволяет моделировать процесс их распознавания. Будучи отражением объективной реальности, понятие образа столь же объективно, как и сама реальность, а поэтому это понятие может быть само по себе объектом специального исследования.
В литературе, посвященной проблеме обучения распознавания образов (ОРО), часто вместо понятия образа вводится понятие класса.
Проблема обучения распознаванию образов (ОРО)
Одним из самых интересных свойств человеческого мозга является способность отвечать на бесконечное множество состояний внешней среды конечным числом реакций. Может быть, именно это свойство позволило человеку достигнуть высшей формы существования живой материи, выражающейся в способности к мышлению, т. е. активному отражению объективного мира в виде образов, понятий, суждений и т. д. Поэтому проблема ОРО возникла при изучении физиологических свойств мозга.
Рассмотрим пример задач из области ОРО.
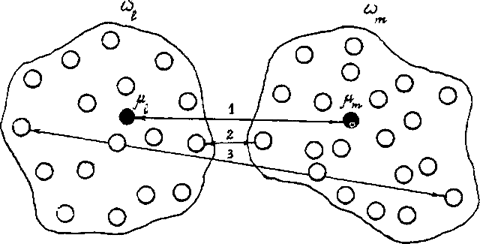
Рис. 1
В целом проблема распознавания образов состоит из двух частей: обучения и распознавания. Обучение осуществляется путем показа отдельных объектов с указанием их принадлежности тому или другому образу. В результате обучения распознающая система должна приобрести способность реагировать одинаковыми реакциями на все объекты одного образа и различными — на все объекты различных образов. Очень важно, что процесс обучения должен завершиться только путем показов конечного числа объектов без каких-либо других подсказок. В качестве объектов обучения могут быть либо картинки, либо другие визуальные изображения (буквы), либо различные явления внешнего мира, например звуки, состояния организма при медицинском диагнозе, состояние технического объекта в системах управления и др. Важно, что в процессе обучения указываются только сами объекты и их принадлежность образу. За обучением следует процесс распознавания новых объектов, который характеризует действия уже обученной системы. Автоматизация этих процедур и составляет проблему обучения распознаванию образов. В том случае, когда человек сам разгадывает или придумывает, а затем навязывает машине правило классификации, проблема распознавания решается частично, так как основную и главную часть проблемы (обучение) человек берет на себя.
Проблема обучения распознаванию образов интересна как с прикладной, так и с принципиальной точки зрения. С прикладной точки зрения решение этой проблемы важно прежде всего потому, что оно открывает возможность автоматизировать многие процессы, которые до сих пор связывали лишь с деятельностью живого мозга. Принципиальное значение проблемы тесно связано с вопросом, который все чаще возникает в связи с развитием идей кибернетики: что может и что принципиально не может делать машина? В какой мере возможности машины могут быть приближены к возможностям живого мозга? В частности, может ли машина развить в себе способность перенять у человека умение производить определенные действия в зависимости от ситуаций, возникающих в окружающей среде? Пока стало ясно только то, что если человек может сначала сам осознать свое умение, а потом его описать, т. е. указать, почему он производит действия в ответ на каждое состояние внешней среды или как (по какому правилу) он объединяет отдельные объекты в образы, то такое умение без принципиальных трудностей может быть передано машине. Если же человек обладает умением, но не может объяснить его, то остается только один путь передачи умения машине — обучение примерами.
Круг задач, которые могут решаться с помощью распознающих систем, чрезвычайно широк. Сюда относятся не только задачи распознавания зрительных и слуховых образов, но и задачи распознавания сложных процессов и явлений, возникающих, например, при выборе целесообразных действий руководителем предприятия или выборе оптимального управления технологическими, экономическими, транспортными или военными операциями. В каждой из таких задач анализируются некоторые явления, процессы, состояния внешнего мира, всюду далее называемые объектами наблюдения. Прежде чем начать анализ какого-либо объекта, нужно получить о нем определенную, каким-либо способом упорядоченную информацию. Такая информация представляет собой характеристику объектов, их отображение на множестве воспринимающих органов распознающей системы.
Но каждый объект наблюдения может воздействовать по-разному, в зависимости от условий восприятия. Например, какая-либо буква, даже одинаково написанная, может в принципе как угодно смещаться относительно воспринимающих органов. Кроме того, объекты одного и того же образа могут достаточно сильно отличаться друг от друга и, естественно, по-разному воздействовать на воспринимающие органы.
Каждое отображение какого-либо объекта на воспринимающие органы распознающей системы, независимо от его положения относительно этих органов, принято называть изображением объекта, а множества таких изображений, объединенные какими-либо общими свойствами, представляют собой образы.
При решении задач управления методами распознавания образов вместо термина "изображение" применяют термин "состояние". Состояние — это определенной формы отображение измеряемых текущих (или мгновенных) характеристик наблюдаемого объекта. Совокупность состояний определяет ситуацию. Понятие "ситуация" является аналогом понятия "образ". Но эта аналогия не полная, так как не всякий образ можно назвать ситуацией, хотя всякую ситуацию можно назвать образом.
Ситуацией принято называть некоторую совокупность состояний сложного объекта, каждая из которых характеризуется одними и теми же или схожими характеристиками объекта. Например, если в качестве объекта наблюдения рассматривается некоторый объект управления, то ситуация объединяет такие состояния этого объекта, в которых следует применять одни и те же управляющие воздействия. Если объектом наблюдения является военная игра, то ситуация объединяет все состояния игры, которые требуют, например, мощного танкового удара при поддержке авиации.
Выбор исходного описания объектов является одной из центральных задач проблемы ОРО. При удачном выборе исходного описания (пространства признаков) задача распознавания может оказаться тривиальной и, наоборот, неудачно выбранное исходное описание может привести либо к очень сложной дальнейшей переработке информации, либо вообще к отсутствию решения. Например, если решается задача распознавания объектов, отличающихся по цвету, а в качестве исходного описания выбраны сигналы, получаемые от датчиков веса, то задача распознавания в принципе не может быть решена.
Геометрический и структурный подходы.
Каждый раз, когда сталкиваются с незнакомыми задачами, появляется естественное желание представить их в виде некоторой легко понимаемой модели, которая позволяла бы осмыслить задачу в таких терминах, которые легко воспроизводятся нашим воображением. А так как мы существуем в пространстве и во времени, наиболее понятной для нас является пространственно-временная интерпретация задач.
Любое изображение, которое возникает в результате наблюдения какого-либо объекта в процессе обучения или экзамена, можно представить в виде вектора, а значит и в виде точки некоторого пространства признаков. Если утверждается, что при показе изображений возможно однозначно отнести их к одному из двух (или нескольких) образов, то тем самым утверждается, что в некотором пространстве существует две (или несколько) области, не имеющие общих точек, и что изображения — точки из этих областей. Каждой такой области можно приписать наименование, т. е. дать название, соответствующее образу.
Проинтерпретируем теперь в терминах геометрической картины процесс обучения распознаванию образов, ограничившись пока случаем распознавания только двух образов. Заранее считается известным лишь только то, что требуется разделить две области в некотором пространстве и что показываются точки только из этих областей. Сами эти области заранее не определены, т. е. нет каких-либо сведений о расположении их границ или правил определения принадлежности точки к той или иной области.
В ходе обучения предъявляются точки, случайно выбранные из этих областей, и сообщается информация о том, к какой области принадлежат предъявляемые точки. Никакой дополнительной информации об этих областях, т. е. о расположении их границ, в ходе обучения не сообщается. Цель обучения состоит либо в построении поверхности, которая разделяла бы не только показанные в процессе обучения точки, но и все остальные точки, принадлежащие этим областям, либо в построении поверхностей, ограничивающих эти области так, чтобы в каждой из них находились только точки одного образа. Иначе говоря, цель обучения состоит в построении таких функций от векторов-изображений, которые были бы, например, положительны на всех точках одного и отрицательны на всех точках другого образа. В связи с тем, что области не имеют общих точек, всегда существует целое множество таких разделяющих функций, а в результате обучения должна быть построена одна из них.
Если предъявляемые изображения принадлежат не двум, а большему числу образов, то задача состоит в построении по показанным в ходе обучения точкам поверхности, разделяющей все области, соответствующие этим образам, друг от друга. Задача эта может быть решена, например, путем построения функции, принимающей над точками каждой из областей одинаковое значение, а над точками из разных областей значение этой функции должно быть различно.
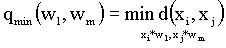
Рис. 2 - Два образа.
На первый взгляд кажется, что знание всего лишь некоторого количества точек из области недостаточно, чтобы отделить всю область. Действительно, можно указать бесчисленное количество различных областей, которые содержат эти точки, и как бы ни была построена по ним поверхность, выделяющая область, всегда можно указать другую область, которая пересекает поверхность и вместе с тем содержит показанные точки. Однако известно, что задача о приближении функции по информации о ней в ограниченном множестве точек, существенно более узкой, чем все множество, на котором функция задана, является обычной математической задачей об аппроксимации функций. Разумеется, решение таких задач требует введения определенных ограничений на классе рассматриваемых функций, а выбор этих ограничений зависит от характера информации, которую может добавить учитель в процессе обучения. Одной из таких подсказок является гипотеза о компактности образов. Интуитивно ясно, что аппроксимация разделяющей функции будет задачей тем более легкой, чем более компактны и чем более разнесены в пространстве области, подлежащие разделению. Так, например, в случае, показанном на Рис. 2а, разделение заведомо более просто, чем в случае, показанном на Рис. 2б. Действительно, в случае, изображенном на Рис. 2а, области могут быть разделены плоскостью, и даже при больших погрешностях в определении разделяющей функции она все же будет продолжать разделять области. В случае же на Рис. 2б, разделение осуществляется замысловатой поверхностью и даже незначительные отклонения в ее форме приводят к ошибкам разделения. Именно это интуитивное представление о сравнительно легко разделимых областях привело к гипотезе компактности.
Наряду с геометрической интерпретацией проблемы обучения распознаванию образов существует и иной подход, который назван структурным, или лингвистическим. Поясним лингвистический подход на примере распознавания зрительных изображений. Сначала выделяется набор исходных понятий — типичных фрагментов, встречающихся на изображениях, и характеристик взаимного расположения фрагментов — "слева", "снизу", "внутри" и т. д. Эти исходные понятия образуют словарь, позволяющий строить различные логические высказывания, иногда называемые предположениями. Задача состоит в том, чтобы из большого количества высказываний, которые могли бы быть построены с использованием этих понятий, отобрать наиболее существенные для данного конкретного случая.
Далее, просматривая конечное и по возможности небольшое число объектов из каждого образа, нужно построить описание этих образов. Построенные описания должны быть столь полными, чтобы решить вопрос о том, к какому образу принадлежит данный объект. При реализации лингвистического подхода возникают две задачи: задача построения исходного словаря, т. е. набор типичных фрагментов, и задача построения правил описания из элементов заданного словаря.
В рамках лингвистической интерпретации проводится аналогия между структурой изображений и синтаксисом языка. Стремление к этой аналогии было вызвано возможностью использовать аппарат математической лингвистики, т. е. методы по своей природе являются синтаксическими. Использование аппарата математической лингвистики для описания структуры изображений можно применять только после того, как произведена сегментация изображений на составные части, т. е. выработаны слова для описания типичных фрагментов и методы их поиска. После предварительной работы, обеспечивающей выделение слов, возникают собственно лингвистические задачи, состоящие из задач автоматического грамматического разбора описаний для распознавания изображений. При этом проявляется самостоятельная область исследований, которая требует не только знания основ математической лингвистики, но и овладения приемами, которые разработаны специально для лингвистической обработки изображений.
Гипотеза компактности
Если предположить, что в процессе обучения пространство признаков формируется исходя из задуманной классификации, то тогда можно надеяться, что задание пространства признаков само по себе задает свойство, под действием которого образы в этом пространстве легко разделяются. Именно эти надежды по мере развития работ в области распознавания образов стимулировали появление гипотезы компактности, которая гласит: образам соответствуют компактные множества в пространстве признаков. Под компактным множеством пока будем понимать некие "сгустки" точек в пространстве изображений, предполагая, что между этими сгустками существуют разделяющие их разряжения.
Однако эту гипотезу не всегда удавалось подтвердить экспериментально, но, что самое главное, те задачи, в рамках которых гипотеза компактности хорошо выполнялась (Рис. 2а), все без исключения находили простое решение. И наоборот, те задачи, для которых гипотеза не подтверждалась (Рис. 2б), либо совсем не решались, либо решались с большим трудом с привлечением дополнительных ухищрений. Этот факт заставил по меньшей мере усомниться в справедливости гипотезы компактности, так как для опровержения любой гипотезы достаточно одного отрицающего ее примера. Вместе с этим, выполнение гипотезы всюду там, где удавалось хорошо решить задачу обучения распознаванию образов, сохраняло к этой гипотезе интерес. Сама гипотеза компактности превратилась в признак возможности удовлетворительного решения задач распознавания.
Формулировка гипотезы компактности подводит вплотную к понятию абстрактного образа. Если координаты пространства выбирать случайно, то и изображения в нем будут распределены случайно. Они будут в некоторых частях пространства располагаться более плотно, чем в других. Назовем некоторое случайно выбранное пространство абстрактным изображением. В этом абстрактном пространстве почти наверняка будут существовать компактные множества точек. Поэтому в соответствии с гипотезой компактности множества объектов, которым в абстрактном пространстве соответствуют компактные множества точек, разумно назвать абстрактными образами данного пространства.
Обучение и самообучение. Адаптация и обучение
Все картинки, представленные на Рис. 1, характеризуют задачу обучения. В каждой из этих задач задается несколько примеров (обучающая последовательность) правильно решенных задач. Если бы удалось подметить некое всеобщее свойство, не зависящее ни от природы образов, ни от их изображений, а определяющее лишь их способность к разделимости, то наряду с обычной задачей обучения распознаванию, с использованием информации о принадлежности каждого объекта из обучающей последовательности тому или иному образу можно было бы поставить иную классификационную задачу — так называемую задачу обучения без учителя. Задачу такого рода на описательном уровне можно сформулировать следующим образом: системе одновременно или последовательно предъявляются объекты без каких-либо указаний об их принадлежности к образам. Входное устройство системы отображает множество объектов на множество изображений и, используя некоторое заложенное в нее заранее свойство разделимости образов, производит самостоятельную классификацию этих объектов. После такого процесса самообучения система должна приобрести способность к распознаванию не только уже знакомых объектов (объектов из обучающей последовательности), но и тех, которые ранее не предъявлялись. Процессом самообучения некоторой системы называется такой процесс, в результате которого эта система без подсказки учителя приобретает способность к выработке одинаковых реакций на изображения объектов одного и того же образа и различных реакций на изображения различных образов. Роль учителя при этом состоит лишь в подсказке системе некоторого объективного свойства, одинакового для всех образов и определяющего способность к разделению множества объектов на образы.
Оказывается, таким объективным свойством является свойство компактности образов. Взаимное расположение точек в выбранном пространстве уже содержит информацию о том, как следует разделить множество точек. Эта информация и определяет то свойство разделимости образов, которое оказывается достаточным для самообучения системы распознаванию образов.
Большинство известных алгоритмов самообучения способны выделять только абстрактные образы, т. е. компактные множества в заданных пространствах. Различие между ними состоит, по-видимому, в формализации понятия компактности. Однако это не снижает, а иногда и повышает ценность алгоритмов самообучения, так как часто сами образы заранее никем не определены, а задача состоит в том, чтобы определить, какие подмножества изображений в заданном пространстве представляют собой образы. Хорошим примером такой постановки задачи являются социологические исследования, когда по набору вопросов выделяются группы людей. В таком понимании задачи алгоритмы самообучения генерируют заранее не известную информацию о существовании в заданном пространстве образов, о которых ранее никто не имел никакого представления.
Кроме того, результат самообучения характеризует пригодность выбранного пространства для конкретной задачи обучения распознаванию. Если абстрактные образы, выделяемые в процессе самообучения, совпадают с реальными, то пространство выбрано удачно. Чем сильнее абстрактные образы отличаются от реальных, тем "неудобнее" выбранное пространство для конкретной задачи.
Обучением обычно называют процесс выработки в некоторой системе той или иной реакции на группы внешних идентичных сигналов путем многократного воздействия на систему внешней корректировки. Такую внешнюю корректировку в обучении принято называть "поощрениями" и "наказаниями". Механизм генерации этой корректировки практически полностью определяет алгоритм обучения. Самообучение отличается от обучения тем, что здесь дополнительная информация о верности реакции системе не сообщается.
Адаптация — это процесс изменения параметров и структуры системы, а возможно, и управляющих воздействий на основе текущей информации с целью достижения определенного состояния системы при начальной неопределенности и изменяющихся условиях работы.
Обучение — это процесс, в результате которого система постепенно приобретает способность отвечать нужными реакциями на определенные совокупности внешних воздействий, а адаптация — это подстройка параметров и структуры системы с целью достижения требуемого качества управления в условиях непрерывных изменений внешних условий.
Обзор методов распознавания образов
Принципы классификации методов распознавания
Распознаванием образов называются задачи построения и применения формальных операций над числовыми или символьными отображениями объектов реального или идеального мира, результаты решения которых отражают отношения эквивалентности между этими объектами. Отношения эквивалентности выражают принадлежность оцениваемых объектов к каким-либо классам, рассматриваемым как самостоятельные семантические единицы.
При построении алгоритмов распознавания классы эквивалентности могут задаваться исследователем, который пользуется собственными содержательными представлениями или использует внешнюю дополнительную информацию о сходстве и различии объектов в контексте решаемой задачи. Тогда говорят о “распознавании с учителем” [145]. В противном случае, т.е. когда автоматизированная система решает задачу классификации без привлечения внешней обучающей информации, говорят об автоматической классификации или “распознавании без учителя”. Большинство алгоритмов распознавания образов требует привлечения весьма значительных вычислительных мощностей, которые могут быть обеспечены только высокопроизводительной компьютерной техникой.
Различные авторы (Барабаш Ю.Л. [15], Васильев В.И. [26], Горелик А.Л., Скрипкин В.А. [37], Дуда Р., Харт П. [45], Кузин Л.Т. [60], Перегудов Ф.И., Тарасенко Ф.П. [99], Темников Ф.Е. [121], Ту Дж., Гонсалес Р. [145], Уинстон П. [126], Фу К. [130], Цыпкин Я.З. [133] и др.) дают различную типологию методов распознавания образов. Одни авторы различают параметрические, непараметрические и эвристические методы, другие - выделяют группы методов, исходя из исторически сложившихся школ и направлений в данной области. Например, в работе [46], в которой дан прекрасный обзор методов распознавания, используется следующая типология методов распознавания образов:
- методы, основанные на принципе разделения;
- статистические методы;
- методы, построенные на основе “потенциальных функций”;
- методы вычисления оценок (голосования);
- методы, основанные на исчислении высказываний, в частности на аппарате алгебры логики.
Подобная типология методов распознавания с той или иной степенью детализации встречается во многих работах по распознаванию. В то же время известные типологии не учитывают одну очень существенную характеристику, которая отражает специфику способа представления знаний о предметной области с помощью какого-либо формального алгоритма распознавания образов. Д.А.Поспелов (1990) выделяет два основных способа представления знаний:
- Интенсиональное представление - в виде схемы связей между атрибутами (признаками).
- Экстенсиональное представление - с помощью конкретных фактов (объекты, примеры).
Интенсиональное представление фиксируют закономерности и связи, которыми объясняется структура данных. Применительно к диагностическим задачам такая фиксация заключается в определении операций над атрибутами (признаками) объектов, приводящих к требуемому диагностическому результату. Интенсиональные представления реализуются посредством операций над значениями атрибутов и не предполагают произведения операций над конкретными информационными фактами (объектами).
В свою очередь, экстенсиональные представления знаний связаны с описанием и фиксацией конкретных объектов из предметной области и реализуются в операциях, элементами которых служат объекты как целостные системы.
Можно провести аналогию между интенсиональными и экстенсиональными представлениями знаний и механизмами, лежащими в основе деятельности левого и правого полушарий головного мозга человека. Если для правого полушария характерна целостная прототипная репрезентация окружающего мира, то левое полушарие оперирует закономерностями, отражающими связи атрибутов этого мира.
Описанные выше два фундаментальных способа представления знаний позволяют предложить следующую классификацию методов распознавания образов:
Интенсиональные методы распознавания образов - методы, основанные на операциях с признаками. Экстенсиональные методы распознавания образов - методы, основанные на операциях с объектами. Необходимо особо подчеркнуть, что с по мнению авторов существование именно этих двух и только двух групп методов распознавания (оперирующих с признаками, и оперирующих с объектами) глубоко закономерно и отражает фундаментальные характеристики взаимодействия Реальности и Сознания. С этой точки зрения ни один из этих методов, взятый отдельно от другого, не позволяет сформировать адекватное отражение Реальности. Стало быть между этими методами существует отношение дополнительности в смысле Н.Бора [19] и перспективные системы распознавания должны обеспечивать реализацию обоих этих методов, а не только какого-либо одного из них.
В приводимой ниже классификации основное внимание уделено формальным методам распознавания образов и поэтому опущено рассмотрение эвристического подхода к распознаванию, получившего полное и адекватное развитие в экспертных системах. По поводу этого подхода ограничимся лишь несколькими замечаниями.
Эвристический подход основывается на трудно формализуемых знаниях и интуиции исследователя. В этом подходе исследователь сам определяет, какую информацию и каким образом нужно использовать для достижения требуемого эффекта распознавания.
ИНТЕНСИОНАЛЬНЫЕ МЕТОДЫ
Отличительной особенностью интенсиональных методов является то, что в качестве элементов операций при построении и применении алгоритмов распознавания образов они используют различные характеристики признаков и их связей. Такими элементами могут быть отдельные значения или интервалы значений признаков, средние величины и дисперсии, матрицы связи признаков и т. п., над которыми производятся действия, выражаемые в аналитической или конструктивной форме. При этом объекты в данных методах не рассматриваются как целостные информационные единицы, а выступают в роли индикаторов для оценки взаимодействия и поведения своих атрибутов.
Группа интенсиональных методов распознавания образов обширна, и ее деление на подклассы носит в определенной мере условный характер.
МЕТОДЫ, ОСНОВАННЫЕ НА ОЦЕНКАХ ПЛОТНОСТЕЙ РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ПРИЗНАКОВ
Эти методы распознавания образов заимствованы из классической теории статистических решений, в которой объекты исследования рассматриваются как реализации многомерной случайной величины, распределенной в пространстве признаков по какому-либо закону [37]. Они базируются на байесовской схеме принятия решений, апеллирующей к априорным вероятностям принадлежности объектов к тому или иному распознаваемому классу и условным плотностям распределения значений вектора признаков. Данные методы сводятся к определению отношения правдоподобия в различных областях многомерного пространства признаков.
Группа методов, основанных на оценке плотностей распределения значений признаков имеет прямое отношение к методам дискриминантного анализа. Байесовский подход к принятию решений и относится к наиболее разработанным в современной статистике так называемым параметрическим методам, для которых считается известным аналитическое выражение закона распределения (в данном случае нормальный закон) и требуется оценить лишь небольшое количество параметров (векторы средних значений и ковариационные матрицы).
К этой группе относится и метод вычисления отношения правдоподобия для независимых признаков. Этот метод, за исключением предположения о независимости признаков (которое в действительности практически никогда не выполняется), не предполагает знания функционального вида закона распределения. Поэтому его можно отнести к непараметрическим [46].
Другие непараметрические методы, применяемые тогда, когда вид кривой плотности распределения неизвестен и нельзя сделать вообще никаких предположений о ее характере, занимают особое положение. К ним относятся известные метод многомерных гистограмм, метод “k-ближайших соседей, метод евклидова расстояния, метод потенциальных функций и др., обобщением которых является метод, получивший название “оценки Парзена” [46]. Эти методы формально оперируют объектами как целостными структурами, но в зависимости от типа задачи распознавания могут выступать и в интенсиональной и в экстенсиональной ипостасях.
Непараметрические методы анализируют относительные количества объектов, попадающих в заданные многомерные объемы, и используют различные функции расстояния между объектами обучающей выборки и распознаваемыми объектами [46]. Для количественных признаков, когда их число много меньше объема выборки, операции с объектами играют промежуточную роль в оценке локальных плотностей распределения условных вероятностей и объекты не несут смысловой нагрузки самостоятельных информационных единиц. В то же время, когда количество признаков соизмеримо или больше числа исследуемых объектов, а признаки носят качественный или дихотомический характер, то ни о каких локальных оценках плотностей распределения вероятностей не может идти речи. В этом случае объекты в указанных непараметрических методах рассматриваются как самостоятельные информационные единицы (целостные эмпирические факты) и данные методы приобретают смысл оценок сходства и различия изучаемых объектов.
Таким образом, одни и те же технологические операции непараметрических методов в зависимости от условий задачи имеют смысл либо локальных оценок плотностей распределения вероятностей значений признаков, либо оценок сходства и различия объектов.
В контексте интенсионального представления знаний здесь рассматривается первая сторона непараметрических методов, как оценок плотностей распределения вероятностей. Многие авторы отмечают, что на практике непараметрические методы типа оценок Парзена работают хорошо [46]. Основными трудностями применения указанных методов считаются необходимость запоминания всей обучающей выборки для вычисления оценок локальных плотностей распределения вероятностей и высокая чувствительность к непредставительности обучающей выборки.
МЕТОДЫ, ОСНОВАННЫЕ НА ПРЕДПОЛОЖЕНИЯХ О КЛАССЕ РЕШАЮЩИХ ФУНКЦИЙ
В данной группе методов считается известным общий вид решающей функции и задан функционал ее качества. На основании этого функционала по обучающей последовательности ищется наилучшее приближение решающей функции [124]. Самыми распространенными являются представления решающих функций в виде линейных и обобщенных нелинейных полиномов. Функционал качества решающего правила обычно связывают с ошибкой классификации.
Основным достоинством методов, основанных на предположениях о классе решающих функций, является ясность математической постановки задачи распознавания, как задачи поиска экстремума [124]. Решение этой задачи нередко достигается с помощью каких-либо градиентных алгоритмов. Многообразие методов этой группы объясняется широким спектром используемых функционалов качества решающего правила и алгоритмов поиска экстремума. Обобщением рассматриваемых алгоритмов, к которым относятся, в частности, алгоритм Ньютона, алгоритмы перцептронного типа и др., является метод стохастической аппроксимации. В отличие от параметрических методов распознавания успешность применения данной группы методов не так сильно зависит от рассогласования теоретических представлений о законах распределения объектов в пространстве признаков с эмпирической реальностью. Все операции подчинены одной главной цели - нахождению экстремума функционала качества решающего правила. В то же время результаты параметрических и рассматриваемых методов могут быть похожими. Как показано выше, параметрические методы для случая нормальных распределений объектов в различных классах с равными ковариационными матрицами приводят к линейным решающим функциям. Отметим также, что алгоритмы отбора информативных признаков в линейных диагностических моделях, можно интерпретировать как частные варианты градиентных алгоритмов поиска экстремума.
Возможности градиентных алгоритмов поиска экстремума, особенно в группе линейных решающих правил, достаточно хорошо изучены. Сходимость этих алгоритмов доказана только для случая, когда распознаваемые классы объектов отображаются в пространстве признаков компактными геометрическими структурами. Однако стремление добиться достаточного качества решающего правила нередко может быть удовлетворено с помощью алгоритмов, не имеющих строгого математического доказательства сходимости решения к глобальному экстремуму [46].
К таким алгоритмам относится большая группа процедур эвристического программирования, представляющих направление эволюционного моделирования. Эволюционное моделирование является бионическим методом, заимствованным у природы. Оно основано на использовании известных механизмов эволюции с целью замены процесса содержательного моделирования сложного объекта феноменологическим моделированием его эволюции.
Известным представителем эволюционного моделирования в распознавании образов является метод группового учета аргументов (МГУА) [46]. В основу МГУА положен принцип самоорганизации, и алгоритмы МГУА воспроизводят схему массовой селекции. В алгоритмах МГУА особым образом синтезируются и отбираются члены обобщенного полинома, который часто называют полиномом Колмогорова-Габора. Этот синтез и отбор производится с нарастающим усложнением, и заранее нельзя предугадать, какой окончательный вид будет иметь обобщенный полином. Сначала обычно рассматривают простые попарные комбинации исходных признаков, из которых составляются уравнения решающих функций, как правило, не выше второго порядка. Каждое уравнение анализируется как самостоятельная решающая функция, и по обучающей выборке тем или иным способом находятся значения параметров составленных уравнений. Затем из полученного набора решающих функций отбирается часть в некотором смысле лучших. Проверка качества отдельных решающих функций осуществляется на контрольной (проверочной) выборке, что иногда называют принципом внешнего дополнения. Отобранные частные решающие функции рассматриваются далее как промежуточные переменные, служащие исходными аргументами для аналогичного синтеза новых решающих функций и т. д. Процесс такого иерархического синтеза продолжается до тех пор, пока не будет достигнут экстремум критерия качества решающей функции, что на практике проявляется в ухудшении этого качества при попытках дальнейшего увеличения порядка членов полинома относительно исходных признаков.
Принцип самоорганизации, положенный в основу МГУА, называют эвристической самоорганизацией, так как весь процесс основывается на введении внешних дополнений, выбираемых эвристически. Результат решения может существенно зависеть от этих эвристик. От того, как разделены объекты на обучающую и проверочную выборки, как определяется критерий качества распознавания, какое количество переменных пропускается в следующий ряд селекции и т. д., зависит результирующая диагностическая модель.
Указанные особенности алгоритмов МГУА свойственны и другим подходам к эволюционному моделированию. Но отметим здесь еще одну сторону рассматриваемых методов. Это - их содержательная сущность. С помощью методов, основанных на предположениях о классе решающих функций (эволюционных и градиентных), можно строить диагностические модели высокой сложности и получать практически приемлемые результаты. В то же время достижению практических целей в данном случае не сопутствует извлечение новых знаний о природе распознаваемых объектов. Возможность извлечения этих знаний, в частности знаний о механизмах взаимодействия атрибутов (признаков), здесь принципиально ограничена заданной структурой такого взаимодействия, зафиксированной в выбранной форме решающих функций. Поэтому максимально, что можно сказать после построения той или иной диагностической модели - это перечислить комбинации признаков и сами признаки, вошедшие в результирующую модель. Но смысл комбинаций, отражающих природу и структуру распределений исследуемых объектов, в рамках данного подхода часто остается нераскрытым.
ЛОГИЧЕСКИЕ МЕТОДЫ
Логические методы распознавания образов базируются на аппарате алгебры логики и позволяют оперировать информацией, заключенной не только в отдельных признаках, но и в сочетаниях значений признаков. В этих методах значения какого-либо признака рассматриваются как элементарные события [46].
В самом общем виде логические методы можно охарактеризовать как разновидность поиска по обучающей выборке логических закономерностей и формирование некоторой системы логических решающих правил (например, в виде конъюнкций элементарных событий), каждое из которых имеет собственный вес. Группа логических методов разнообразна и включает методы различной сложности и глубины анализа. Для дихотомических (булевых) признаков популярными являются так называемые древообразные классификаторы, метод тупиковых тестов, алгоритм “Кора” и другие. Более сложные методы основываются на формализации индуктивных методов Д.С.Милля. Формализация осуществляется путем построения квазиаксиоматической теории и базируется на многосортной многозначной логике с кванторами по кортежам переменной длины [46].
Алгоритм “Кора”, как и другие логические методы распознавания образов, является достаточно трудоемким, поскольку при отборе конъюнкций необходим полный перебор. Поэтому при применении логических методов предъявляются высокие требования к эффективной организации вычислительного процесса, и эти методы хорошо работают при сравнительно небольших размерностях пространства признаков и только на мощных компьютерах.
ЛИНГВИСТИЧЕСКИЕ (СТРУКТУРНЫЕ) МЕТОДЫ
Лингвистические методы распознавания образов основаны на использовании специальных грамматик порождающих языки, с помощью которых может описываться совокупность свойств распознаваемых объектов [130].
Для различных классов объектов выделяются непроизводные (атомарные) элементы (подобразы, признаки) и возможные отношения между ними. Грамматикой называют правила построения объектов из этих непроизводных элементов [130]. Таким образом, каждый объект представляется совокупностью непроизводных элементов, “соединенных” между собой теми или иными способами или, другими словами, “предложением” некоторого “языка”. Авторы хотели бы особо подчеркнуть очень значительную на их взгляд мировоззренческую ценность этой мысли. Путем синтаксического анализа (грамматического разбора) “предложения” устанавливается его синтаксическая “правильность” или, что эквивалентно, - может ли некоторая фиксированная грамматика (описывающая класс) породить имеющееся описание объекта. Грамматический разбор производится так называемым “синтаксическим анализатором”, который представляет полное синтаксическое описание объекта в виде дерева грамматического разбора, если объект является синтаксически правильным (принадлежит классу, описываемому данной грамматикой). В противном случае, объект либо отклоняется, либо подвергается анализу с помощью других грамматик, описывающих другие классы объектов. Известны бесконтекстные, автоматные и другие типы грамматик. Однако задача восстановления (определения) грамматик по некоторому множеству высказываний (предложений - описаний объектов), порождающих данный язык, является трудно формализуемой. В литературе приводится описание эвристических правил автоматического восстановления грамматик для конструирования и применения лингвистических алгоритмов распознавания образов.
ЭКСТЕНСИОНАЛЬНЫЕ МЕТОДЫ
В методах данной группы, в отличие от интенсионального направления, каждому изучаемому объекту в большей или меньшей мере придается самостоятельное диагностическое значение. По своей сути эти методы близки к клиническому подходу, который рассматривает людей не как проранжированную по тому или иному показателю цепочку объектов, а как целостные системы, каждая из которых индивидуальна и имеет особенную диагностическую ценность [46]. Такое бережное отношение к объектам исследования не позволяет исключать или утрачивать информацию о каждом отдельном объекте, что происходит при применении методов интенсионального направления, использующих объекты только для обнаружения и фиксации закономерностей поведения их атрибутов.
Основными операциями в распознавании образов с помощью обсуждаемых методов являются операции определения сходства и различия объектов. Объекты в указанной группе методов играют роль диагностических прецедентов. При этом в зависимости от условий конкретной задачи роль отдельного прецедента может меняться в самых широких пределах от главной до весьма косвенного участия в процессе распознавания. В свою очередь, условия задачи могут требовать для успешного решения участия различного количества диагностических прецедентов от одного в каждом распознаваемом классе до полного объема выборки, а также разных способов вычисления мер сходства и различия объектов. Этими требованиями объясняется дальнейшее разделение экстенсиональных методов на подклассы.
МЕТОД СРАВНЕНИЯ С ПРОТОТИПОМ
Это наиболее простой экстенсиональный метод распознавания. Он применяется, например, тогда, когда распознаваемые классы отображаются в пространстве признаков компактными геометрическими группировками. В таком случае обычно в качестве точки - прототипа выбирается центр геометрической группировки класса (или ближайший к центру объект). Для классификации неизвестного объекта находится ближайший к нему прототип, и объект относится к тому же классу, что и этот прототип. Очевидно, никаких обобщенных образов классов в данном методе не формируется.
В качестве меры близости могут применяться различные типы расстояний. Часто для дихотомических признаков используется расстояние Хэмминга, которое в данном случае равно квадрату евклидова расстояния. При этом решающее правило классификации объектов эквивалентно линейной решающей функции.
Указанный факт следует особо отметить. Он наглядно демонстрирует связь прототипной и признаковой репрезентации информации о структуре данных. Пользуясь приведенным представлением, можно, например, любую традиционную измерительную шкалу, являющуюся линейной функцией от значений дихотомических признаков, рассматривать как гипотетический диагностический прототип. В свою очередь, если анализ пространственной структуры распознаваемых классов позволяет сделать вывод об их геометрической компактности, то каждый из этих классов достаточно заменить одним прототипом который, фактически эквивалентен линейной диагностической модели.
На практике, конечно, ситуация часто бывает отличной от описанного идеализированного примера. Перед исследователем, намеревающимся применить метод распознавания, основанный на сравнении с прототипами диагностических классов, встают непростые проблемы. Это, в первую очередь, выбор меры близости (метрики), от которого может существенно измениться пространственная конфигурация распределения объектов. И, во-вторых, самостоятельной проблемой является анализ многомерных структур экспериментальных данных. Обе эти проблемы особенно остро встают перед исследователем в условиях высокой размерности пространства признаков, характерной для реальных задач.
МЕТОД K-БЛИЖАЙШИХ СОСЕДЕЙ
Метод k-ближайших соседей для решения задач дискриминантного анализа был впервые предложен еще в 1952 году. Он заключается в следующем. При классификации неизвестного объекта находится заданное число (k) геометрически ближайших к нему в пространстве признаков других объектов (ближайших соседей) с уже известной принадлежностью к распознаваемым классам. Решение об отнесении неизвестного объекта к тому или иному диагностическому классу принимается путем анализа информации об этой известной принадлежности его ближайших соседей, например, с помощью простого подсчета голосов.
Первоначально метод k-ближайших соседей рассматривался как непараметрический метод оценивания отношения правдоподобия. Для этого метода получены теоретические оценки его эффективности в сравнении с оптимальным байесовским классификатором. Доказано, что асимптотические вероятности ошибки для метода k-ближайших соседей превышают ошибки правила Байеса не более чем в два раза.
Как отмечалось выше, в реальных задачах часто приходится оперировать объектами, которые описываются большим количеством качественных (дихотомических) признаков. При этом размерность пространства признаков соизмерима или превышает объем исследуемой выборки. В таких условиях удобно интерпретировать каждый объект обучающей выборки, как отдельный линейный классификатор. Тогда тот или иной диагностический класс представляется не одним прототипом, а набором линейных классификаторов. Совокупное взаимодействие линейных классификаторов дает в итоге кусочно-линейную поверхность, разделяющую в пространстве признаков распознаваемые классы. Вид разделяющей поверхности, состоящей из кусков гиперплоскостей, может быть разнообразным и зависит от взаимного расположения классифицируемых совокупностей.
Также можно использовать другую интерпретацию механизмов классификации по правилу k-ближайших соседей. В ее основе лежит представление о существовании некоторых латентных переменных, абстрактных или связанных каким-либо преобразованием с исходным пространством признаков. Если в пространстве латентных переменных попарные расстояния между объектами такие же, как и в пространстве исходных признаков, и количество этих переменных значительно меньше числа объектов, то интерпретация метода k-ближайших соседей может рассматриваться под углом зрения сравнения непараметрических оценок плотностей распределения условных вероятностей. Приведенное здесь представление о латентных переменных близко по своей сути к представлению об истинной размерности и другим представлениям, используемым в различных методах снижения размерности.
При использовании метода k-ближайших соседей для распознавания образов исследователю приходится решать сложную проблему выбора метрики для определения близости диагностируемых объектов. Эта проблема в условиях высокой размерности пространства признаков чрезвычайно обостряется вследствие достаточной трудоемкости данного метода, которая становится значимой даже для высокопроизводительных компьютеров. Поэтому здесь так же, как и в методе сравнения с прототипом, необходимо решать творческую задачу анализа многомерной структуры экспериментальных данных для минимизации числа объектов, представляющих диагностические классы.
По мнению авторов необходимость уменьшения числа объектов в обучающей выборке (диагностических прецедентов)является недостатком данного метода, т.к. уменьшает представительность обучающей выборки.
АЛГОРИТМЫ ВЫЧИСЛЕНИЯ ОЦЕНОК (ГОЛОСОВАНИЯ)
Принцип действия алгоритмов вычисления оценок (АВО) состоит в вычислении приоритете (оценок сходства), характеризующих “близость” распознаваемого и эталонных объектов по системе ансамблей признаков, представляющей собой систему подмножеств заданного множества признаков.
В отличие от всех ранее рассмотренных методов алгоритмы вычисления оценок принципиально по-новому оперируют описаниями объектов. Для этих алгоритмов объекты существуют одновременно в самых разных подпространствах пространства признаков. Класс АВО доводит идею использования признаков до логического конца: поскольку не всегда известно, какие сочетания признаков наиболее информативны, то в АВО степень сходства объектов вычисляется при сопоставлении всех возможных или определенных сочетаний признаков, входящих в описания объектов [46].
Используемые сочетания признаков (подпространства) авторы называют опорными множествами или множествами частичных описаний объектов. Вводится понятие обобщенной близости между распознаваемым объектом и объектами обучающей выборки (с известной классификацией), которые называют эталонными объектами. Эта близость представляется комбинацией близостей распознаваемого объекта с эталонными объектами, вычисленных на множествах частичных описаний. Таким образом, АВО является расширением метода k-ближайших соседей, в котором близость объектов рассматривается только в одном заданном пространстве признаков.
Еще одним расширением АВО является то, что в данных алгоритмах задача определения сходства и различия объектов формулируется как параметрическая и выделен этап настройки АВО по обучающей выборке, на котором подбираются оптимальные значения введенных параметров. Критерием качества служит ошибка распознавания, а параметризуется буквально все:
- правила вычисления близости объектов по отдельным признакам,
- правила вычисления близости объектов в подпространствах признаков,
- степень важности того или иного эталонного объекта как диагностического прецедента,
- значимость вклада каждого опорного множества признаков в итоговую оценку сходства распознаваемого объекта с каким-либо диагностическим классом.
Параметры АВО задаются в виде значений порогов и (или) как веса указанных составляющих. Теоретические возможности АВО превышают или, по крайней мере, не ниже возможностей любого другого алгоритма распознавания образов, так как с помощью АВО могут быть реализованы все мыслимые операции с исследуемыми объектами. Но, как это обычно бывает, расширение потенциальных возможностей наталкивается на большие трудности их практического воплощения, особенно на этапе построения (настройки) алгоритмов данного типа. Отдельные трудности отмечались ранее при обсуждении метода k-ближайших соседей, который можно было интерпретировать как усеченный вариант АВО. Его тоже можно рассматривать в параметрическом виде и свести задачу к поиску взвешенной метрики выбранного типа. В то же время уже здесь для высокоразмерных задач возникают сложные теоретические вопросы и проблемы, связанные с организацией эффективного вычислительном процесса. Для АВО, если попытаться использовать потенциальные возможности данных алгоритмов в полном объеме, указанные трудности возрастают многократно.
Отмеченные проблемы объясняют то, что на практике применение АВО для решения высокоразмерных задач сопровождается введением каких-либо эвристических ограничений и допущений. В частности, известен пример использования АВО в психодиагностике, в котором апробирована разновидность АВО, фактически эквивалентная методу k-ближайших соседей.
КОЛЛЕКТИВЫ РЕШАЮЩИХ ПРАВИЛ
Заканчивая обзор методов распознавания образов, остановимся еще на одном подходе. Это так называемые коллективы решающих правил.
Так как различные алгоритмы распознавания проявляют себя по-разному на одной и той же выборке объектов, то закономерно встает вопрос о синтетическом решающем правиле, адаптивно использующем сильные стороны этих алгоритмов. В синтетическом решающем правиле применяется двухуровневая схема распознавания. На первом уровне работают частные алгоритмы распознавания, результаты которых объединяются на втором уровне в блоке синтеза. Наиболее распространенные способы такого объединения основаны на выделении областей компетентности того или иного частного алгоритма. Простейший способ нахождения областей компетентности заключается в априорном разбиении пространства признаков исходя из профессиональных соображений конкретной науки (например, расслоение выборки по некоторому признаку). Тогда для каждой из выделенных областей строится собственный распознающий алгоритм. Другой способ базируется на применении формального анализа для определения локальных областей пространства признаков как окрестностей распознаваемых объектов, для которых доказана успешность работы какого-либо частного алгоритма распознавания.
Самый общий подход к построению блока синтеза рассматривает результирующие показатели частных алгоритмов как исходные признаки для построения нового обобщенного решающего правила. В этом случае могут использоваться все перечисленные выше методы интенсионального и экстенсионального направлений в распознавании образов. Эффективными для решения задачи создания коллектива решающих правил являются логические алгоритмы типа “Кора” и алгоритмы вычисления оценок (АВО), положенные в основу так называемого алгебраического подхода, обеспечивающего исследование и конструктивное описание алгоритмов распознавания, в рамки которого укладываются все существующие типы алгоритмов [46].
КРИТЕРИИ КАЧЕСТВА МЕТОДОВ РАСПОЗНАВАНИЯ
Приведенные характеристики различных методов распознавания образов были бы неполными без обсуждения вопроса о критериях качества алгоритмов и о способах оценки этих критериев. Показателями качества обычно являются либо собственно ошибка классификации, либо связанные с ней некоторые функции потерь. При этом различают условную вероятность ошибочной классификации, ожидаемую ошибку алгоритма классификации на выборке заданного объема и асимптотическую ожидаемую ошибку классификации. Функции потерь также разделяют на функцию средних потерь, функцию ожидаемых потерь и эмпирическую функцию средних потерь.
Для оценки выбранного показателя качества того или иного алгоритма распознавания образов применяется три основных экспериментальных способа.
- Выборка используется одновременно как обучающая и контрольная;
- Выборка разбивается на две части - обучающую и контрольную;
- Из всей выборки случайным образом извлекается один объект, а по оставшимся синтезируется решающее правило и производится распознавание извлеченного объекта. Процедура повторяется заданное число раз (например, до полного перебора).
Первый способ дает завышенную оценку качества распознавания по сравнению с той же оценкой качества по независимым от обучения данным. Второй способ является самым простым и убедительным. Им широко пользуются, если экспериментальных данных достаточно. В то же время третий способ, называемый также методом скользящего экзамена является наиболее предпочтительным, так как дает меньшую дисперсию оценки вероятности ошибки. Однако этот метод является и самым трудоемким, так как требует многократного построения правила распознавания.
Применительно к рассмотренным методам распознавания образов эта трудоемкость наиболее существенна для многих методов интенсионального направления, для которых необходимо на каждом шаге скользящего экзамена производить коррекцию используемых характеристик признаков и их связей (например, средних значений и ковариаций). Но для экстенсиональных методов, оперирующих объектами, достаточно просто не включать контрольный объект в исследуемое правило распознавания. Поэтому данные методы (k-ближайших соседей, АВО) как бы приспособлены для реализации метода скользящего экзамена, который позволяет избегать расточительного обращения с экспериментальным материалом и одновременно получать наиболее эффективные оценки качества распознающих алгоритмов.
Сравнение описанных выше методов распознавания образов приводит к следующим выводам. Для решения реальных задач из группы методов интенсионального направления практическую ценность представляют параметрические методы и методы, основанные на предложениях о виде решающих функций. Параметрические методы составляют основу традиционной методологии конструирования показателей. Применение этих методов в реальных задачах связано с наложением сильных ограничений на структуру данных, которые приводят к линейным диагностическим моделям с очень приблизительными оценками их параметров. При использовании методов, основанных на предположениях о виде решающих функций, исследователь также вынужден обращаться к линейным моделям. Это обусловлено высокой размерностью пространства признаков, характерной для реальных задач, которая при повышении степени полиноминальной решающей функции дает огромный рост числа ее членов при проблематичном сопутствующем повышении качества распознавания. Таким образом, спроецировав область потенциального применения интенсиональных методов распознавания на реальную проблематику, получим картину, соответствующую хорошо отработанной традиционной методологии линейных диагностических моделей.
Как отмечалось ранее, свойства линейных диагностических моделей, в которых диагностический показатель представлен взвешенной суммой исходных признаков, хорошо изучены. Результаты этих моделей (при соответствующем нормировании) интерпретируются как расстояния от исследуемых объектов до некоторой гиперплоскости в пространстве признаков или, что эквивалентно, как проекции объектов на некоторую прямую линию в данном пространстве. Поэтому линейные модели адекватны только простым геометрическим конфигурациям областей пространства признаков, в которые отображаются объекты разных диагностических классов. При более сложных распределениях эти модели принципиально не могут отражать многие особенности структуры экспериментальных данных. В то же время такие особенности способны нести ценную диагностическую информацию.
Вместе с тем, появление в какой-либо реальной задаче простых многомерных структур (в частности, многомерных нормальных распределений) следует скорее расценивать как исключение, чем как правило. Часто диагностические классы формируются на основании сложносоставных внешних критериев, что автоматически влечет за собой геометрическую неоднородность данных классов в пространстве признаков. Это особенно касается “жизненных”, наиболее часто практически встречающихся критериев. В таких условиях применение линейных моделей фиксирует только самые “грубые” закономерности экспериментальной информации.
Применение экстенсиональных методов не связано каким-либо предположениями о структуре экспериментальной информации кроме того, что внутри распознаваемых классов должны существовать одна или несколько групп чем-то похожих объектов, а объекты разных классов должны чем-то отличаться друг от друга. Очевидно при любой конечной размерности обучающей выборки (а другой она быть и не может) это требование выполняется всегда просто по той причине, что существуют случайные различия между объектами. В качестве мер сходства применяются различные меры близости (расстояния) объектов в пространстве признаков. Поэтому эффективное использование экстенсиональных методов распознавания образов зависит от того, насколько удачно определены указанные меры близости, а также от того, какие объекты обучающей выборки (объекты с известной классификацией) выполняют роль диагностических прецедентов. Успешное решение данных задач дает результат, приближающийся к теоретически достижимым пределам эффективности распознавания.
Достоинствам экстенсиональных методов распознавания образов противопоставлена, в первую очередь, высокая техническая сложность их практического воплощения. Для высокоразмерных пространств признаков внешне простая задача нахождения пар ближайших точек превращается в серьезную проблему. Также многие авторы отмечают в качестве проблемы необходимость запоминания достаточно большого количества объектов, представляющих распознаваемые классы.
По мнению авторов, само по себе это не является проблемой, однако воспринимается как проблема (например, в методе k-ближайших соседей) по той причине, что при распознавании каждого объекта происходит полный перебор всех объектов обучающей выборки.
Теоретические проблемы применения экстенсиональных методов распознавания связаны с проблемами поиска информативных групп признаков, нахождения оптимальных метрик для измерения сходства и различия объектов и анализа структуры экспериментальной информации. В то же время успешное решение перечисленных проблем позволяет не только конструировать эффективные распознающие алгоритмы, но и осуществлять переход от экстенсионального знания эмпирических фактов к интенсиональному знанию о закономерностях их структуры.
Переход от экстенсионального знания к интенсиональному происходит на той стадии, когда формальный алгоритм распознавания уже сконструирован и продемонстрировал свою эффективность. Тогда производится изучение механизмов, за счет которых достигается полученная эффективность. Такое изучение, связанное с анализом геометрической структуры данных, может, например, привести к выводу, что достаточно заменить объекты, представляющие тот или иной диагностический класс, одним типичным представителем (прототипом). Это эквивалентно, как отмечалось выше, заданию традиционной линейной диагностической шкалы. Также возможно, что каждый диагностический класс достаточно заменить несколькими объектами, осмысленными как типичные представители некоторых подклассов, что эквивалентно построению веера линейных шкал. Возможны и другие варианты, которые будут рассмотрены ниже.
Таким образом обзор методов распознавания показывает, что в настоящее время теоретически разработан целый ряд различных методов распознавания образов. В литературе приводится развернутая их классификация. Однако для большинства этих методов их программная реализация отсутствует, и это глубоко закономерно, можно даже сказать “предопределено” характеристиками самих методов распознавания. Об этом можно судить потому, что такие системы мало упоминаются в специальной литературе, других общедоступных источниках информации.
Следовательно остается недостаточно разработанным вопрос о практической применимости тех или иных теоретических методов распознавания для решения практических задач при реальных (т.е. довольно значительных) размерностях данных и на реальных современных компьютерах.
Вышеупомянутое обстоятельство может быть понято, если напомнить, что сложность математической модели экспоненциально увеличивает трудоемкость программной реализации системы и в такой же степени уменьшает шансы на то, что эта система будет практически работать. Это означает, что реально на рынке можно реализовать только такие программные системы, в основе которых лежат достаточно простые и “прозрачные” математические модели. Поэтому разработчик, заинтересованный в тиражировании своего программного продукта, подходит к вопросу о выборе математической модели не с чисто научной точки зрения, а как прагматик, с учетом возможностей программной реализации. Он считает, что модель должна быть как можно проще, а значит реализоваться с меньшими затратами и более качественно, а также должна обязательно работать (быть практически эффективной).
В этой связи особенно актуальной представляется задача реализации в системах распознавания механизма обобщения описаний объектов, относящихся к одному классу, т.е. механизм формирования компактных обобщенных образов. Очевидно, что такой механизм обобщения позволит “сжать” любую по размерности обучающую выборку к заранее известной по размерности базе обобщенных образов.
В заключение краткого обзора методов распознавания представим суть вышеизложенного в сводной таблице, а также в форме в виде диаграмы:
1. классификация методов распознавания;
2. области применения методов распознавания;
3. классификация ограничений методов распознавания.
СВОДНАЯ ТАБЛИЦА КЛАССИФФИКАЦИИ МЕТОДОВ РАСПОЗНАВАНИЯ, СРАВНЕНИЯ ИХ ОБЛАСТЕЙ ПРИМЕНЕНИЯ И ОГРАНИЧЕНИЙ (НЕДОСТАТКОВ)
|
Классификация
методов распознавани |
Область
применения |
Ограничения
(недостатки) |
||
|
Методы распознавания
|
Интенсиальные методы
|
Методы, основанные на оценках
плотностей распределения значений признаков (или сходства и различия
объектов)
|
Задачи с известным распределением,
как правило нормальным, необходимость набора большой
статистики.
|
Отсутствие обобщения.
Необходимость перебора всей обучающей выборки при распознавании, высокая
чувствительность к непредставительности обучающей
выборки и артефактам.
|
|
Методы, основанные на
предположениях о классе решающих функций
|
Классы должны
быть хорошо разделяемыми, система признаков - ортонормированной.
|
Отсутствие обобщения. Должен быть
заранее известен вид решающей функции. Невозможность учета новых знаний о
корреляциях между признаками.
|
||
|
Логические методы
|
Задачи небольшой размерности
пространства признаков.
|
Отсутствие обобщения. При отборе
логических решающих правил (коньюнкций) необходим
полный перебор. Высокая вычислительная трудоемкость.
|
||
|
Лингвистические (структурные)
методы
|
Задачи небольшой размерности пространства
признаков.
|
Отсутствие обобщения. Задача
восстановления (определения) грамматики по некоторому множеству высказываний
(описаний объектов), является трудно формализуемой. Нерешенность
теоретических проблем.
|
||
|
Экстенсиальные методы
|
Метод сравнения с прототипом
|
Задачи небольшой размерности
пространства признаков.
|
Отсутствие обобщения. Высокая
зависимость результатов классификации от меры расстояния (метрики).
|
|
|
Метод k-ближайших соседей
|
Задачи небольшой размерности по количеству
классов и признаков.
|
Отсутствие обобщения. Высокая
зависимость результатов классификации от меры расстояния (метрики).
Необходимость полного перебора обучающей выборки при распознавании.
Вычислительная трудоемкость.
|
||
|
Алгоритмы вычисления оценок
(голосования) АВО |
Задачи небольшой размерности по
количеству классов и признаков.
|
Отсутствие обобщения. Зависимость
результатов классификации от меры расстояния (метрики). Необходимость полного
перебора обучающей выборки при распознавании. Высокая техническая сложность
метода.
|
||
|
Коллективы решающих правил
|
Задачи небольшой размерности по
количеству классов и признаков.
|
Отсутствие обобщения. Очень
высокая техническая сложность метода, нерешенность ряда теоретических проблем,
как при определении областей компетенции частных методов, так и в самих
частных методах.
|
||
АНАЛИЗ ПЕРСПЕКТИВНЫХ НАПРАВЛЕНИЙ РАЗВИТИЯ МЕТОДОВ РАСПОЗНАВАНИЯ
Анализ перспективных направлений развития методов распознавания показывает, что для успешного достижения цели исследования необходимо решить (или обойти) следующие проблемы:
комбинаторного взрыва;
достижения независимости времени распознавания от размерности обучающей выборки;
корректного снижения размерности пространства признаков без существенной потери содержащейся в них значимой информации;
достижения высокой валидности результатов анализа.
Первая и вторая проблемы имеют сходное происхождение и возникают при попытке прямого перебора вариантов кластеризации и во многих методах распознавания.
Третья - при выявлении наиболее существенного и отбрасывании относительно несущественного в созданных Системой образах. Аналогичную проблему решает художник, когда переносит на двумерный холст изображение трехмерного пейзажа, причем так, чтобы при этом сохранилась максимальная узнаваемость этого пейзажа. Практически работающее программное средство, реализующее данную функцию, должно корректно понижать размерность пространства описания от нескольких тысяч, до сотен или даже десятков признаков. На практике снижение размерности пространства признаков сводится к двум задачам: во-первых определение ценности признаков для решения задачи распознавания, и, во-вторых, отбрасывание незначимых признаков. Сделать это корректно не так просто в связи с тем, что все признаки, вообще говоря, взаимосвязаны и ценность одних признаков может меняться весьма значительно при отбрасывании других, даже несущественных признаков.
Четвертая - при разработке такой математической модели и программной реализации Системы, которые бы обеспечивали наиболее высокий уровень соответствия существа выполняемых Системой операций, моделирующих процессы восприятия и познания (а также их результатов) интуитивному пониманию пользователем и экспертом подобных процессов в психике человека. Из опыта математического эксперимента известно, что результаты кластерного анализа и даже идентификации к сожалению слишком часто не соответствуют представлениям человека-эксперта о данной предметной области, хотя и соответствуют логике математической модели. Это означает, что такие модели обладают низкой внешней валидностью, т.е. не отражают существо тех процессов обработки информации, с помощью которых нормальный компетентный человек и в нормальном состоянии сознания реализует аналогичные когнитивные функции. Следовательно, перспективная математическая модель и ее программная реализация должны обеспечивать интуитивно понятную содержательную интерпретацию при применении в тех предметных областях, в которых у человека-эксперта имеется развитая и адекватная реальности система ориентации. По мнению авторов, именно применение такого рода моделей можно считать корректным, т.к. в противном случае трудно сказать, как можно применить результаты их работы. Данный подход позволяет обоснованно надеяться на то, что и в новых малоизученных областях такая модель даст корректные результаты и удовлетворит потребности познающего человека в той или иной предметной области.
Уместно отметить, что многие перспективные разработки систем распознавания ориентируются на еще не созданные перспективные вычислительные системы или на очень мощные, а значит редкие, дорогие и недоступные для массового пользователя компьютеры. Это обстоятельство переводит подобные разработки в категорию фундаментальных научных исследований, которые в настоящее время в реальных условиях мало кем могут быть реально использованы.
Кластерный анализ
Кластерный анализ предназначен для разбиения множества объектов на заданное или неизвестное число классов на основании некоторого математического критерия качества классификации (cluster (англ.) — гроздь, пучок, скопление, группа элементов, характеризуемых каким-либо общим свойством). Критерий качества кластеризации в той или иной мере отражает следующие неформальные требования:
а) внутри групп объекты должны быть тесно связаны между собой;
б) объекты разных групп должны быть далеки друг от друга;
в) при прочих равных условиях распределения объектов по группам должны быть равномерными.
Требования а) и б) выражают стандартную концепцию компактности классов разбиения; требование в) состоит в том, чтобы критерий не навязывал объединения отдельных групп объектов.
Узловым моментом в кластерном анализе считается выбор метрики (или меры близости объектов), от которого решающим образом зависит окончательный вариант разбиения объектов на группы при заданном алгоритме разбиения. В каждой конкретной задаче этот выбор производится по-своему, с учетом главных целей исследования, физической и статистической природы используемой информации и т. п. При применении экстенсиональных методов распознавания, как было показано в предыдущих разделах, выбор метрики достигается с помощью специальных алгоритмов преобразования исходного пространства признаков.
Другой важной величиной в кластерном анализе является расстояние между целыми группами объектов. Приведем примеры наиболее распространенных расстояний и мер близости, характеризующих взаимное расположение отдельных групп объектов. Пусть wi — i-я группа (класс, кластер) объектов, Ni — число объектов, образующих группу wi, вектор m i — среднее арифметическое объектов, входящих в wi (другими словами [m i — “центр тяжести” i-й группы), a q ( wl, wm ) — расстояние между группами wl и wm
Рис. 1. Различные способы определения расстояния между кластерами wl и wm: 1 — по центрам тяжести, 2 — по ближайшим объектам, 3 — по самым далеким объектам Рис 1.

Рис. 1
Расстояние ближайшего соседа есть расстояние между ближайшими объектами кластеров:
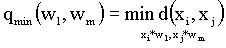
Расстояние дальнего соседа — расстояние между самыми дальними объектами кластеров:
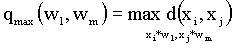
Расстояние центров тяжести равно расстоянию между центральными точками кластеров:
Обобщенное (по Колмогорову) расстояние между классами, или обобщенное K-расстояние, вычисляется по формуле
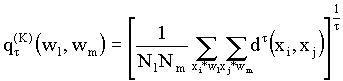
В частности, при t a µ и при t a -µ имеем
Выбор той или иной меры расстояния между кластерами влияет, главным образом, на вид выделяемых алгоритмами кластерного анализа геометрических группировок объектов в пространстве признаков. Так, алгоритмы, основанные на расстоянии ближайшего соседа, хорошо работают в случае группировок, имеющих сложную, в частности, цепочечную структуру. Расстояние дальнего соседа применяется, когда искомые группировки образуют в пространстве признаков шаровидные облака. И промежуточное место занимают алгоритмы, использующие расстояния центров тяжести и средней связи, которые лучше всего работают в случае группировок эллипсоидной формы.
Нацеленность алгоритмов кластерного анализа на определенную структуру группировок объектов в пространстве признаков может приводить к неоптимальным или даже неправильным результатам, если гипотеза о типе группировок неверна. В случае отличия реальных распределений от гипотетических указанные алгоритмы часто "навязывают" данным не присущую им структуру и дезориентируют исследователя. Поэтому экспериментатор, учитывающий данный факт, в условиях априорной неопределенности прибегает к применению батареи алгоритмов кластерного анализа и отдает предпочтение какому-либо выводу на основании комплексной оценки совокупности результатов работы этих алгоритмов.
Алгоритмы кластерного анализа отличаются большим разнообразием. Это могут быть, например, алгоритмы, реализующие полный перебор сочетаний объектов или осуществляющие случайные разбиения множества объектов. В то же время большинство таких алгоритмов состоит из двух этапов. На первом этапе задается начальное (возможно, искусственное или даже произвольное) разбиение множества объектов на классы и определяется некоторый математический критерий качества автоматической классификации. Затем, на втором этапе, объекты переносятся из класса в класс до тех пор, пока значение критерия не перестанет улучшаться.
Многообразие алгоритмов кластерного анализа обусловлено также множеством различных критериев, выражающих те или иные аспекты качества автоматического группирования. Простейший критерий качества непосредственно базируется на величине расстояния между кластерами. Однако такой критерий не учитывает "населенность" кластеров — относительную плотность распределения объектов внутри выделяемых группировок. Поэтому другие критерии основываются на вычислении средних расстояний между объектами внутри кластеров. Но наиболее часто применяются критерии в виде отношений показателей "населенности" кластеров к расстоянию между ними. Это, например, может быть отношение суммы межклассовых расстояний к сумме внутриклассовых (между объектами) расстояний или отношение общей дисперсии данных к сумме внутриклассовых дисперсий и дисперсии центров кластеров.
Функционалы качества и конкретные алгоритмы автоматической классификации достаточно полно и подробно рассмотрены в специальной литературе. Эти функционалы и алгоритмы характеризуются различной трудоемкостью и подчас требуют ресурсов высокопроизводительных компьютеров. Разнообразные процедуры кластерного анализа входят в состав практически всех современных пакетов прикладных программ для статистической обработки многомерных данных.
Иерархическое группирование

Классификационные процедуры иерархического типа предназначены для получения наглядного представления о стратификационной структуре всей исследуемой совокупности объектов. Эти процедуры основаны на последовательном объединении кластеров (агломеративные процедуры) и на последовательном разбиении (дивизимные процедуры). Наибольшее распространение получили агломеративные процедуры. Рассмотрим последовательность операций в таких процедурах.
На первом шаге все объекты считаются отдельными кластерами. Затем на каждом последующем шаге два ближайших кластера объединяются в один. Каждое объединение уменьшает число кластеров на один так, что в конце концов все объекты объединяются в один кластер. Наиболее подходящее разбиение выбирает чаще всего сам исследователь, которому предоставляется дендрограмма, отображающая результаты группирования объектов на всех шагах алгоритма (Рис). Могут одновременно также использоваться и математические критерии качества группирования.
Различные варианты определения расстояния между кластерами дают различные варианты иерархических агломеративных процедур. Учитывая специфику подобных процедур, для задания расстояния между классами оказывается достаточным указать порядок пересчета расстояний между классом wl и классом w(m, n) являющимся объединением двух других классов wm и wn по расстояниям qmn = q(wm, wn) и qln = q(wl, wn) между этими классами. В литературе предлагается следующая общая формула для вычисления расстояния между некоторым классом wl и классом w(m, n):
ql(m, n) = q (wl,
w(m, n))
= a qlm
+ b qln
+ g qmn
+ d | qlm
- qln |
где a , b , g и d — числовые коэффициенты, определяющие нацеленность агломеративной процедуры на решение той или иной экстремальной задачи. В частности, полагая a = b = -d = 1/2 и g = 0, приходим к расстоянию, измеряемому по принципу ближайшего соседа. Если положить a = b = d = 1/2 и g = 0, то расстояние между двумя классами определится как расстояние между двумя самыми далекими объектами этих классов, то есть это будет расстояние дальнего соседа. И, наконец, выбор коэффициентов соотношения по формулам
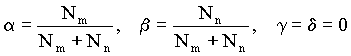
приводит к расстоянию qcp между классами, вычисленному как среднее расстояние между всеми парами объектов, один из которых берется из одного класса, а другой из другого.
Использование следующей модификации формулы
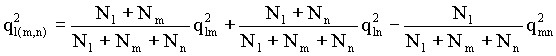
дает агломеративный алгоритм, приводящий к минимальному увеличению общей суммы квадратов расстояний между объектами внутри классов на каждом шаге объединения этих классов. В отличие от оптимизационных кластерных алгоритмов предоставляющих исследователю конечный результат группирования объектов, иерархические процедуры позволяют проследить процесс выделения группировок и иллюстрируют соподчиненность кластеров, образующихся на разных шагах какого-либо агломеративного или дивизимного алгоритма. Это стимулирует воображение исследователя и помогает ему привлекать для оценки структуры данных дополнительные формальные и неформальные представления.
