Источник: http://www.softcraft.ru/auto/etc/avn/avn2.shtml
Введение
В предыдущей статье я рассказал о понятии "параллельных цифровых автоматов" (ПЦА). Все там было так классно описано, а вот примера не было ни одного... Этот недостаток я решил исправить в данном опусе. Будет показан параллельный алгоритм и подготовка к синтезу (собственно синтез в универсальном базисе "И", "ИЛИ", "НЕ" и с использованием языка описания аппаратуры VHDL будет показан в следующей статье - уж больно объемной выходит эта...).
Параллельный алгоритм
Самый понятный для нас способ описания алгоритма - это граф-схема алгоритма (ГСА). Давайте для примера возьмем нечто абстрактное - для начала так будет проще. Любители конкретных примеров - не волнуйтесь, в будущем рассмотрим что-нибудь совсем реальное :-)! Ну а теперь - рис. 1.
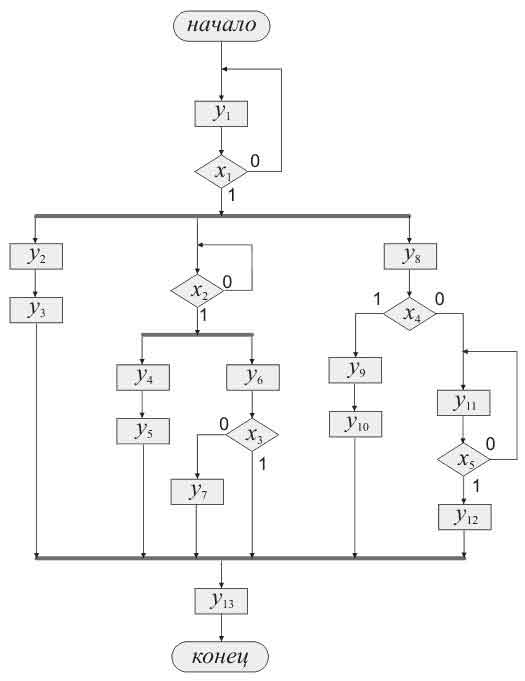
Рис. 1 Граф-схема некоторого алгоритма
Итак, необходимо построить устройство с алгоритмом работы, показанном выше. Устройство принимает входные сигналы x1, x2, ..., x5. Результатом работы являются выходные сигналы y1, y2, ..., y13. Вначале работы, после выполнения условия x1, идет распараллеливание - появляются новые потоки. Все они выполняются со своими циклами. Внутри порождаются еще два потока. Потом они все объединются в один поток. Объединение происходит когда... Кстати, действительно, когда? Самое простое - дождаться окончания работы всех потоков. Но можно дождаться первого потока, а остальным дать доработать. А можно и не давать доработать...
Эти размышления показывают, что все не так просто, как хотелось бы. Есть разные виды синхронизации работы. А есть еще и флаги, семафоры, мьютексы... Много чего есть! Но на этом останавливаться в этой работе я не буду. Тут пока ограничимся самой простой синхронизацией - будем дожидаться конца работы всех потоков ("все" - это те потоки, которые в конце ограничены одной линией - "синхронизатором") .
Итак, алгоритм понятен, переходим к подготовке к синтезу.
Переход к диаграмме состояний
Первым делом нам необходимо перейти к состояниям, так как цифровой автомат базируется именно на них.
Есть два основных метода формирования состояний и, фактически, двух разных типов автомата,- автомат Мили и автомат Мура. Чтобы было проще (напоминаю, что цель - показать синтез, а не закапываться в подробности), выберем автомат Мура.
Для КЦА Мура правила отметки состояний следующие: 1) отмечаем состоянием a1 первую и последнюю вершину ("начало" и "конец"), 2) отмечаем a2, a3, ... все последующие операторные вершины. Полученные отметки соединяются также, как и в ГСА, но с учетом условных вершин. В результате получается диаграмма состояний.
Очевидно, что в ПЦА все будет несколько иначе. В чем будет разница?
Прежде всего нам явно необходимо выделить потоки. Процесс прост (пока не будем углубляться в дебри определений - процесс действительно прост и очевиден!).
Вот что у нас получилось:
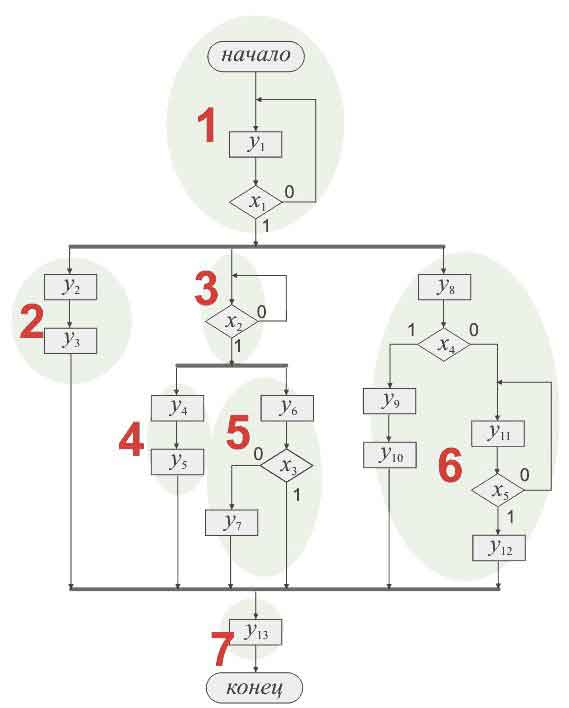
Рис. 2 Алгоритм с выделенными потоками
Каждый поток - это самый что ни на есть обыкновенный последовательный цифровой автомат! Следовательно, для него осхраняются все правила разметки состояний, последующего кодирования состояний, оптимизации и так далее. Впрочем, есть один момент. При отметке состояний КЦА последнее и начальное состояние отмечается как одно - a1. Так ли это в нашем случае?
Каждый поток может прибывать в двух состояниях - рабочее и нерабочее. Если рабочее, то идет обычная смена состояний. Если нерабочее - то это или ожидание начала работы или ожидание конца при синхронизации (2-ой поток закончится явно раньше 4-го, 5-го и 6-го - отож ему и придется ждать конца их работы).
Попробуем сделать отметку по этим принципам. Попробовали? Тогда смотрите рисунок 3:
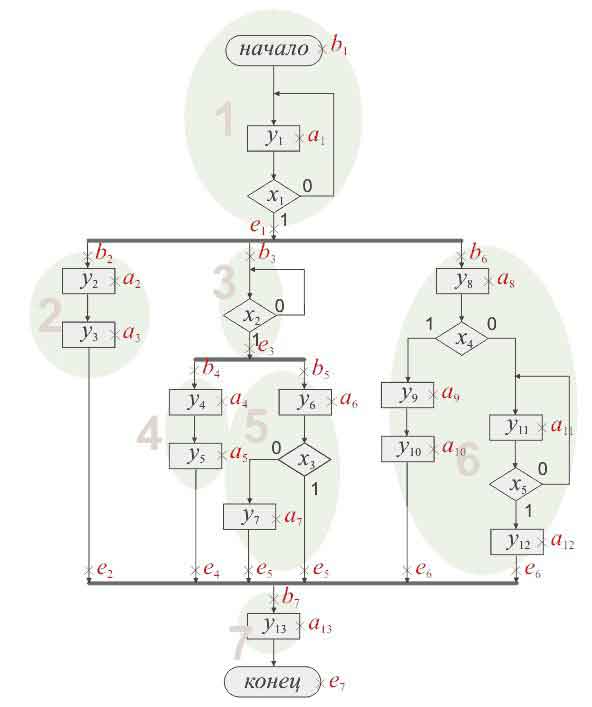
Составим таблицу с расчетом необходимых размеров памяти:

Итого требуется 2+2+1+2+2+3+2=14 бит памяти.
Можно объединить потоки 1-ый и 7-ой. Все получается вполне логично - у КЦА работа начинается и заканчивается одним и тем же состоянием. Фактически КЦА всегда зациклен. А объединение этих потоков и соединение состояний b1 и e7 вполне удовлетворяет этому условию. Таким образом, уберем седьмой поток. Очевидно, что произойдут изменения в состояниях:
b1 - это состояние объединяется с e7. Следуя традиции разметки состояний, назовем его a1;
a1 - переназовем в a14;
e1 - остается;
b7 - переназовем в b1;
a13 - оставим нетронутым;
e7 - уже упразднили :-).
Таким образом, мы получаем новую разметку состояний:

Рис. 4 Алгоритм с отмеченными состояниями (отпимизировано)
Теперь мы перейдем к диаграмме состояний. Пока что не будем описывать условия перехода вершин b и e - об этом будет сказано дальше. В этой диаграмме будут присутствовать квазинезависимые :-) КЦА. Но связь между ними как раз и будет заключаться в условиях переходов вышеназванных вершин. Диаграмма состояний показана ниже: