Актуальность темы
Для современных систем радиосвязи характерным является окончательный переход средств радиосвязи на сигналы с применением программной перестройки рабочей частоты (ППРЧ) и организации связи в сети с временным доступом [28]. Особое внимание в современных сетях радиосвязи уделяется повышению защищенности от организованных преднамеренных помех; скрытности передачи любых видов информации, ее засекречиванию; гибкому доступу абонентов различных приоритетов к необходимым и доступным только для данной категории пользователей данным; увеличению количества каналов связи; обеспечению ЭМС со всеми другими существующими и разрабатываемыми РЭС. Применение новых сигналов непременно ведет к расширению направлений его использования [26].
Примером такой системы может быть система радиосвязи, описанная в [30].
Структура сигнала обнаружения имеет вид пачки длительностью 
, состоящей из периодической последовательности информационных радиоимпульсов длительностью 
и периодом следования
. Внутреннее заполнение импульсов представляет собой информационную посылку, манипулированную по фазе (ФМн). Несущая частота каждого радиоимпульса изменяется по псевдослучайному закону с определенным шагом перестройки в заданном диапазоне рабочих частот (ППРЧ). Выход на связь каждого абонента осуществляется в течение отведенного ему стандартного временного интервала (СВИ), длительностью
T.
Уникальный характер таких систем радиосвязи, их широкие возможности определяются структурой сигнала и нетрадиционными методами организации обмена информацией [28].
Цель работы – исследование приёмника обнаружения на основе j-корреляционной обработки сигналов. Основной задачей приёмника является эффективное обнаружение ФМн сигналов с ППРЧ. Для достижения поставленной задачи необходимо провести:
Методы исследования. При проведении исследований используются методы статистической радиотехники, теория корреляционной обработки, положения теории сигналов и процессов в радиотехнике, методы оптимального приёма и метод анализа модели с использованием виртуальной программной среды LabVIEW.
Краткий обзор широкоизвестных методов обнаружения
Как правило, сигнал, действующий на входе приемника s(t), характеризуется множеством параметров, изменяющихся по случайному закону, таких как: амплитуда, начальная фаза, закон перестройки частоты, время действия сигнала на входе приемника и другие. Чем больше неизвестных параметров, тем сложнее создать приёмник обнаружения.
Анализ методов обнаружения в известной литературе всегда начинается с анализа теории оптимального обнаружения. И хотя этот метод крайне редко используется на практике, его параметры являются предельными и позволяют дать оценку возможностей других методов [8].
Корреляционный приёмник полностью известного сигнала
Пусть на входе приёмника действует сигнал s(t) и аддитивный гауссов белый шум n(t). В результате чего образуется сумма
 |
(1.1) |
Качество приемника обнаружения оценивается минимальным отношением сигнал-шум на входе, при заданном отношении сигнал-шум на выходе. Уровень шумового напряжения на выходе приемника определяется шумовыми свойствами линейного тракта.
Математическое ожидание сигнала на выходе приёмника при отсутствии полезного сигнала на входе равно математическому ожиданию белого шума
 |
(1.2) |
Математическое ожидание при наличии сигнала на входе определяется
 |
(1.3)[3] |
Отсюда параметр обнаружения приёмника, определяющий соотношение сигнал-шум
 |
(1.4) |
Ожидаемый сигнал s(t) – ФМн сигнал с ППРЧ.
Основным этапом при обработке принятого колебания является вычисление интеграла
 |
(1.5) |
Для получения интеграла z необходимы априорные сведения о параметрах сигнала для создания точной его копии s(t) на приёмной стороне.
Схема, вычисляющая интеграл (1.5) приведено на рисунке 1 [4]. И как показано в [3] обеспечивает максимальное отношение сигнал-шум (1.4.) на выходе приемника, поэтому такое устройство получило название оптимальный приёмник. В его состав входят коррелятор, интегратор, вычисляющий z, и пороговое устройство, в котором выходное значение интегратора z сравнивается с порогом z0.
Рисунок 1. Структурная схема корреляционного приёмника.
Корреляционный приёмник обладает рядом преимуществ по сравнение с другими приёмниками обнаружения, что позволяет получить наилучшее значение отношения сигнал-шум. Из отмеченного, а также из результатов анализа данных в [1, 3, 4, 5, 8, 11] следует, что данный приёмник требует априорных сведений о принимаемом сигнале.
Данный недостаток отводит данному приёмнику роль идеализированной модели приёмника обнаружения в теории оптимальной обработке сигналов. Как отмечает [8] полученные результаты следует рассматривать как теоретический верхний предел для характеристик обнаружения.
Корреляционный приёмник обнаружения для сигнала с неизвестной начальной фазой
Анализ так называемого оптимального приемника, проводится из условия заранее известной начальной фазы, т. е. известного времени прихода сигнала на вход приемника обнаружения. Однако, в реальной ситуации время прихода сигнала, как правило, не известно, да и не может быть известной по ряду объективных причин. Так в случае движущейся цели фаза сигнала будет переменной величиной. Если изменяющуюся фазу обозначить через
D(t), то в случае использования в качестве приемника обнаружения оптимального приемника опорному сигналу
s(t) надо задавать всевозможные начальные фазы и лишь для одной из них корреляционная обработка даст максимальный уровень в выходном сигнале, т.е. окажется оптимальной. Такая многократная процедура установления начальных фаз в опорном сигнале существенно усложняет приёмник обнаружения [2].
Однако без неё можно обойтись, если воспользоваться ортогональными составляющими опорного сигнала, представив их в виде
 |
(2.1) |
|
где |
(2.2) |
Для ортогональных составляющих s1(t) и s2(t) и принимаемого сигнала х(t) вычисляются корреляционные интегралы
 |
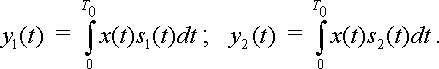(2.3) |
Функция взаимной корреляции принимаемого сигнала х(t) и ожидаемого сигнала s(t), равна
 |
(2.4) |
где 0 – начальная фаза опорного сигнала.
Так как речь идет об ортогональных составляющих, то y1 и y2 есть проекции вектора сигнала на координатные оси, тогда
 |
(2.5) |
Тогда величины y1/Y и y2/Y по модулю не превышают единицу, а сумма их квадратов равна единице, то одна из них принимается за синус, другая – за косинус некоторого угла , откуда
 |
(2.6)[2] |
Таким образом, оптимальный приёмник для сигналов с неизвестной начальной фазой непосредственно выполняет операции над входным сигналом x(t), определяемые формулами (2.1) и (2.3), и состоит из двух параллельно включённых корреляторов, выходные сигналы которых объединяются в квадратуре (рис.2) [1].
Рисунок 2. Структурная схема оптимального корреляционного приёмника при неизвестной начальной фазе.
В корреляторах вычисляются величины y1 и y2, а после объединения – огибающая Y. Для оптимального приёмника для сигнала с неизвестной фазой требуется несколько большее пороговое отношение сигнал-шум по сравнения с корреляционным приёмником для сигнала с полностью известными параметрами [4].
В виду того, что начальная фаза принимаемого сигнала, не единственный параметр, априорные сведения о котором отсутствуют – этот приёмник также следует рассматривать как идеализированную модель.
Наряду с корреляционным приёмником используется фильтрационные приёмники, оптимальные для принимаемых сигналов.
Согласованный фильтр
Известно, что реакция линейного фильтра на входное воздействие x(t) описывается интегралом Дюамеля
 |
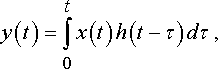(3.1) |
где 
– импульсная характеристика фильтра
Сопоставление интеграла Дюамеля (3.1) с корреляционным интегралом (1.5) указывает на их сходство.
Интеграл (3.1) выполняет функцию взаимной корреляции, импульсная характеристика которого с точностью до постоянного множителя k0 является зеркальным отображением полезного сигнала. Такой фильтр называют согласованным. Структурная схема приемника с согласованным фильтром (СФ) представлена на рисунке 3 [2]
Рисунок 3. Структурная схема оптимального приёмника с согласованным фильтром.
Согласно теории согласованной фильтрации частотная характеристика фильтра является комплексно-сопряжённой функцией входного сигнала с точностью до постоянного множителя [3]. Фазочастотная характеристика фильтра СФ обеспечивает накопление максимального пикового значения сигнала. Отличительной чертой СФ по сравнению с корреляционным приёмником является инвариантность относительно задержки сигнала. В литературе также отмечается его согласованность для сигналов с неизвестной амплитудой. Отношение сигнал-шум на выходе СФ зависит только от энергии полезного сигнала и спектральной плотности шума. Ни один другой фильтр, кроме согласованного фильтра, не может дать большее соотношение сигнал-шум [2].
В известной литературе отмечается не целесообразность использования СФ для сложных сигналов. ФМн сигналы с ППРЧ относят к сложным сигналам повышенной скрытности. И как следствие практическое применение СФ в приемнике обнаружения не возможно [30].
Квазиоптимальный фильтр с рециркулятором
Применение теории согласованной фильтрации на практике значительно усложняется при усложнении вида сигнала, поэтому используют фильтры, которые согласованы по определённым параметрам. Такие фильтры называют квазиоптимальные.
Рециркуляционная схема (рис.4) как отмечено [1,3,8] позволяет эффективно накапливать периодически повторяющиеся импульсы сигналов.
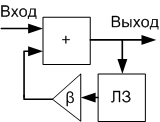
Рисунок 4. Структурная схема рециркулятора.
Не смотря на то, что ФМн сигнал с ППРЧ передаётся в виде пачки импульсов, обнаружить сигнал на радиочастоте не удаётся. Как показано в [2] это связано с фазовым рассогласованием входной пачки импульсов с рециркуляционным циклом накопления.
Для возможности выделения сигнала без согласования фазы выделение сигнала осуществляют на видеочастоте. На выходе линейного тракта ставится амплитудный детектор, выделяющий огибающую и обеспечивающий её постоянство в пределах периода высокой частоты [4]. Схема квазиоптимального приёмника обнаружения с рециркулятором приведена на рисунке 5.
Рисунок 5. Структурная схема квазиоптимального приёмника с рециркулятором.
Квазиоптимальный приёмник обнаружения с рециркулятором позволяет обнаружить ФМн сигнал с ППРЧ только на видеочастоте. К недостаткам рассматриваемого приёмника обнаружения следует также отнести повышенные требования к энергетическим характеристикам сигнала, что уменьшает вероятность правильного обнаружения сигнала, при заданном уровне ложной тревоги [4].
На рисунке 6 представлена обобщённая схема результатов анализа известных методов обнаружения.
Рисунок 6. Обобщенная схема результатов анализа известных методов обнаружения.
(Данный рисунок является анимацией. Объем файла: 53 Кбайт; размер: 497 × 307 пикселей; количество кадров:
5; количество циклов повторения: бесконечно).
Выводы
Проведенный анализ существующих методов обнаружения показал, что единственным методом способным обеспечить обнаружение сигнала с ППРЧ это приемник обнаружения с рециркулятором. Этот приёмник в то же время имеет ряд ограничений в использовании при обнаружении сигналов с ППРЧ. Альтернативные идеи методов обнаружения могут дать толчок в развитии этой области. Именно принципиально новый подход необходим при рассмотрении J-корреляционного приёмника обнаружения.
Список использованных источников
Замечание. В данный момент выпускная работа находится на стадии разработки, поэтому изложенный материал может незначительно отличаться от текста, изложенного в пояснительной записке. Более подробную информацию об исследованиях j-корреляционного приемника обнаружения можно получить после декабря 2011 года у автора этой работы только с письменного разрешения научного руководителя.
