RUS | UKR | ENG | ДонНТУ > Портал магістрів ДонНТУ
Магістр ДонНТУ Фунтиков Максим Миколайович

Фунтиков Максим Миколайович

Факультет радіотехніки та спеціальної підготовки

Кафедра радіотехніки та захисту інформації

Спеціальность: Радіоелектронні пристрої, системи та комплекси

Тема магістерської роботи:

Дослідження приймача виявлення на основі j-кореляційної обробки сигналів.

Науковий керівник: д.т.н. Сорочан Анатолій Григорович

Резюме | Реферат | Біографія | Iндівідуальний розділ

Реферат з теми магістерської роботи

Актуальність теми

Для сучасних систем радіозв'язку характерним є остаточний перехід засобів радіозв'язку на сигнали із застосуванням програмної перебудови робочої частоти (ППРЧ) і організації зв'язку в мережі з часовим доступом [28]. Особлива увага в сучасних мережах радіозв'язку приділяється підвищенню захищеності від організованих навмисних перешкод; скритності передачі будь-яких видів інформації, її засекречуванню; гнучкому доступу абонентів різних пріоритетів до необхідних і доступних тільки для даної категорії користувачів даним; збільшенню кількості каналів зв'язки; забезпеченню ЕМС із усіма іншими існуючими й розроблювальними РЕС. Застосування нових сигналів неодмінно веде до розширення напрямків його використання [26].

Прикладом такої системи може бути система радіозв'язку, яка описана в [30].

Структура сигналу виявлення має вигляд пачки тривалістю , що складається з періодичної послідовності інформаційних радіоімпульсів тривалістю та періодом проходження . Внутрішнє заповнення імпульсів являє собою інформаційну посилку, маніпульовану по фазі (ФМн). Несуча частота кожного радіоімпульсу змінюється за псевдовипадковим законом з певним кроком перебудови в заданому діапазоні робочих частот (ППРЧ). Вихід на зв'язок кожного абонента здійснюється протягом відведеного йому стандартного часового інтервалу (СЧІ), тривалістю T.

Унікальний характер таких систем радіозв'язку, їх широкі можливості визначаються структурою сигналу й нетрадиційними методами організації обміну інформацією [28].

Ціль роботи – дослідження приймача виявлення на основі j кореляційної обробки сигналів. Основною задачею приймача є ефективне виявлення ФМн сигналів із ППРЧ. Для досягнення поставленої задачі необхідно провести:

  1. Аналіз існуючих методів виявлення.
  2. На підставі проведеного аналізу вибрати метод виявлення, який щонайкраще дозволяє розв'язати поставлену задачу.
  3. Дослідження обраного приймача виявлення, визначити його основні параметри, виявити переваги й недоліки.
  4. Порівняльний аналіз обраного приймача виявлення із широковідомими приймачами.

Методи дослідження. При проведенні досліджень використовуються методи статистичної радіотехніки, теорія кореляційної обробки, положення теорії сигналів і процесів у радіотехніці, методи оптимального прийому та метод аналізу моделі з використанням віртуального програмного середовища LabVIEW.

Короткий огляд широковідомих методів виявлення:

Як правило, сигнал, що діє на вході приймача s(t), характеризується множиною параметрів, що змінюються за випадковим законом, такі як: амплітуда, початкова фаза, закон перебудови частоти, час дії сигналу на вході приймача й інші. Чим більше невідомих параметрів, тем складніше створити приймач виявлення.

Аналіз методів виявлення у відомій літературі завжди починається з аналізу теорії оптимального виявлення. І хоча цей метод украй рідко використовується на практиці, його параметри є граничними й дозволяють дати оцінку можливостей інших методів [8].

Кореляційний приймач повністю відомого сигналу

Нехай на вході приймача діють сигнал s(t) і адитивний гаусів білий шум n(t). У результаті чого утворюється сума

(1.1)

Якість приймача виявлення оцінюється мінімальним відношенням сигнал-шум на вході, при заданому відношенні сигнал-шум на виході. Рівень шумової напруги на виході приймача обумовлюється шумовими властивостями лінійного тракту.

Математичне очікування сигналу на виході приймача при відсутності корисного сигналу на вході дорівнює математичному очікуванню білого шуму

(1.2)

Математичне очікування при наявності сигналу на вході визначається

(1.3)[3]

Звідси параметр виявлення приймача, що визначає співвідношення сигнал-шум

(1.4)

Очікуваний сигнал s(t) – ФМн сигнал із ППРЧ.

Основним етапом при обробці прийнятого коливання є обчислення інтеграла

(1.5)

Для одержання інтеграла z необхідні апріорні відомості про параметри сигналу для створення точної його копії s(t) на приймальній стороні.

Схема, що обчислює інтеграл (1.5) приведена на рисунку 1 [4]. І як показано в [3] забезпечує максимальне відношення сигнал-шум (1.4) на виході приймача, тому такий пристрій отримав назву оптимальний приймач. До його складу входять корелятор, інтегратор, що обчислює z, і пороговий пристрій (ПУ), у якому вихідне значення інтегратора z порівнюється з порогом z0.

Рисунок 1. Структурная схема корреляционного приёмника

Рисунок 1. Структурна схема кореляційного приймача

Кореляційний приймач має ряд переваг у порівняння з іншими приймачами виявлення, що дозволяє отримати найкраще значення відношення сигнал-шум. З відзначеного, а також з результатів аналізу даних в [1, 3, 4, 5, 8, 11] прямує, що даний приймач вимагає апріорних відомостей про прийнятий сигнал.

Даний недолік відводить даному приймачу роль ідеалізованої моделі приймача виявлення в теорії оптимальній обробці сигналів. Як відзначає [8] отримані результати слід розглядати як теоретичну верхню межу для характеристик виявлення.

Кореляційний приймач виявлення для сигналу з невідомою початковою фазою

Аналіз так званого оптимального приймача, проводиться з умови заздалегідь відомої початкової фази, тобто відомого часу приходу сигналу на вхід приймача виявлення. Однак, у реальній ситуації час приходу сигналу, як правило, не відомо, та й не може бути відомий з ряду об'єктивних причин. Так у випадку рухомої цілі фаза сигналу буде змінною величиною. Якщо мінливу фазу позначити через D(t), то у випадку використання як приймача виявлення оптимального приймача опорному сигналу s(t) необхідно задавати всілякі початкові фази й лише для однієї з них кореляційна обробка дасть максимальний рівень у вихідному сигналі, тобто виявиться оптимальною. Така многократна процедура встановлення початкових фаз в опорному сигналі суттєво ускладнює приймач виявлення [2].

Однак без неї можна обійтися, якщо скористатися ортогональними складовими опорного сигналу, представив їх у вигляді

(2.1)
   

де     

(2.2)

Для ортогональних складових s1(t), s2(t) і прийнятого сигналу х(t) обчислюються кореляційні інтеграли

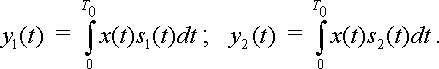(2.3)

Функція взаємної кореляції прийнятого сигналу х(t) і очікуваного сигналу s(t), дорівнює

(2.4)

де 0 – початкова фаза опорного сигналу.

Тому що мова йде про ортогональні складові, то y1 та y2 є проекції вектора сигналу на координатні осі, тоді

(2.5)

Тоді величини y1/Y та y2/Y по модулю не перевищують одиниці, а сума їх квадратів дорівнює одиниці, то одна з них приймається за синус, інша – за косинус деякого кута , звідки

(2.6)[2]

Таким чином, оптимальний приймач для сигналів з невідомою початковою фазою безпосередньо виконує операції над вхідним сигналом x(t), обумовлені формулами (2.1) і (2.3), і складається із двох паралельно включених кореляторів, вихідні сигнали яких об'єднуються у квадратурі (рис.2) [1].

Рисунок 2. Структурная схема оптимального корреляционного приёмника при неизвестной начальной фазе.

Рисунок 2. Структурна схема оптимального кореляційного приймача при невідомій початковій фазі.

У кореляторах обчислюються величини y1 та y2, а після об'єднання – огинаючу Y. Для оптимального приймача для сигналу з невідомою фазою потрібно дещо більше граничне відношення сигнал-шум по порівняння з кореляційним приймачем для сигналу з повністю відомими параметрами [4].

Приймаючи до уваги те, що початкова фаза прийнятого сигналу, не єдиний параметр, апріорні відомості про який відсутні – цей приймач також слід розглядати як ідеалізовану модель.

Поряд з кореляційним приймачем використовується фільтраційні приймачі, оптимальні для прийнятих сигналів

Узгоджений фільтр

Відомо, що реакція лінійного фільтра на вхідний вплив x(t) описується інтегралом Дюамеля

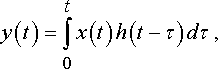(3.1)

де – імпульсна характеристика

Інтеграл (3.1) виконує функцію взаємної кореляції, імпульсна характеристика якого з точністю до постійного множника k0 є дзеркальним відображенням корисного сигналу. Такий фільтр називають узгоджений. Структурна схема приймача з узгоджений фільтром (УФ) представлено на рисунку 3 [2]

Рисунок 3. Структурна схема оптимального приймача з УФ (СФ).

Згідно з теорією узгодженої фільтрації частотна характеристика фільтра є комплексно-сполученою функцією вхідного сигналу з точністю до постійного множника [3]. Фазочастотна характеристика фільтра УФ забезпечує накопичення максимального пікового значення сигналу. Розпізнавальною рисою УФ у порівнянні з кореляційним приймачем є інваріантність щодо затримки сигналу. У літературі також відмічається його узгодженість для сигналів з невідомою амплітудою. Відношення сигнал-шум на виході УФ залежить тільки від енергії корисного сигналу й спектральної щільності шуму. Жоден інший фільтр, крім узгодженого фільтра, не може дати більше співвідношення сигнал-шум [2].

У відомій літературі відмічається не доцільність використання УФ для складних сигналів. ФМн сигнали із ППРЧ відносять до складних сигналів підвищеної скритності. І як наслідок практичний застосування УФ у приймачі виявлення не можливо [30].

Квазіоптимальний фільтр із рециркулятором

Застосування теорії узгодженої фільтрації на практиці значно ускладнюється при ускладненні виду сигналу, тому використовують фільтри, які узгоджені з певними параметрами. Такі фільтри називають квазіоптимальними.

Рециркуляційна схема (рис.4) як відзначено [1,3,8] дозволяє ефективно накопичувати періодично повторювані імпульси сигналів.

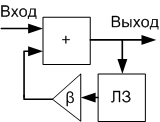
Рисунок 4. Структурна схема рециркулятора (ЛЗ - лінія затримки).

Незважаючи на те, що ФМн сигнал із ППРЧ передається у вигляді пачки імпульсів, виявити сигнал на радіочастоті не вдається. Як показано в [2] це пов'язане з фазовою неузгодженістю вхідної пачки імпульсів з рециркуляційним циклом накопичення.

Для можливості виділення сигналу без узгодження фази виділення сигналу здійснюють на відеочастоті. На виході лінійного тракту ставиться амплітудний детектор, що виділяє огинаючу і забезпечує її сталість у межах періоду високої частоти [4]. Схема квазіоптимального приймача виявлення з рециркулятором наведено на рисунку 5.

Рисунок 5. Структурна схема квазіоптимального приймача із рециркулятором (линейный тракт - лінійний тракт, амплитудный детектор - амплітудний детектор, рециркулятор - рециркулятор, пороговое устройство - пороговий пристрій).

Квазіоптимальний приймач виявлення з рециркулятором дозволяє виявити ФМн сигнал із ППРЧ тільки на відеочастоті. До недоліків розглянутого приймача виявлення слід також віднести підвищені вимоги до енергетичних характеристик сигналу, що зменшує ймовірність правильного виявлення сигналу, при заданому рівні помилкової тривоги [4].

На рисунку 6 представлена Узагальнена схема результатів аналізу відомих методів виявлення.

Обобщенная схема результатов анализа известных методов обнаружения

Рисунок 6. Узагальнена схема результатів аналізу відомих методів виявлення. (помехи - перешкоди, корреляционный приёмник - кореляційний приймач, корреляционный приёмник обнаружения для сигнала с неизвестной начальной фазой - кореляційний приймач виявлення для сигналу з невідомою початковою фазою, согласованный фильтр - узгодженний фільтр, квазиоптимальный фильтр с рециркулятором - квазіоптимальний фільтр із рециркулятором).

(Даний рисунок є анімацією. Обсяг файлу: 53 Кбайт; розміри: 497 × 307 пікселів; кількість кадрів: 5; кількість циклів повторення: бескінечно).

Висновки

Проведений аналіз існуючих методів виявлення показав, що єдиним методом здатним забезпечити виявлення сигналу із ППРЧ є приймач виявлення з рециркулятором. Цей приймач у той же час має ряд обмежень у використанні при виявленні сигналів із ППРЧ. Альтернативні ідеї методів виявлення можуть дати поштовх у розвитку цієї області. Саме новий підхід необхідний при розгляді J-кореляційного приймача виявлення.

Список використаних джерел

  1. Дулевич В. Е., Коростылёв А. А., Клюев Н. Ф., Мельник Ю. А. и др. – Теоретические основы радиолокации: Учебное пособие для вузов. – 2 изд. М.: Сов. Радио, 1978. – 608 с.
  2. Финкельштейн М. И. – Основы радиолокации: Учебник для вузов. – 2 изд., М.: Радио и связь, 1983. – 536 с.
  3. Ширман Я. Д. и др. Радиоэлектронные системы: Основы построения и теория. Справочник – М.: Радиотехника, 2007. – 512 с.
  4. Сосулин Ю. Г. Теоретические основы радиолокации и радионавигации: Учебное пособие для вузов. М.: Радио и связь, 1992. – 304 с.
  5. Казаринов Ю. М. и др. Радиотехнические системы. Учебник для вузов. – М.: Высш. шк., 1990. – 496 с.
  6. Ширман Я. Д., Манжос В. Н. – Теория и техника обработки радиолокационной информации на фоне помех. – М.: Радио и связь, 1981. – 416 с.
  7. Алексеев А. И., Шереметьев А. Г., Тузов Г. И., Глазов Б. И. Теория и применение псевдослучайных сигналов. – М.: «Наука», 1969.
  8. Тихонов В. И. Оптимальный приём сигналов. – М.: Радио и связь, 1983. – 320 с.
  9. Мазора Ю. Л., Мачусский Е. А., Правда В. И. Радиотехника: Энциклопедия – М.: «Додэка-ХХI», 2002. – 944 с.
  10. Левин Б. Р. Теоретические основы статистической радиотехники. – 3-е изд., – М.: Радио и связь, 1989. – 656 с.
  11. Гуткин Л. С. Теория оптимальных методов радиоприема при флуктуационных помехах. Изд. 2-е, М.: «Советское радио», 1972. – 448 с.
  12. Скляр, Бернард. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е испр.: Пер. с англ. – М.: Издательский дом «Вильямс», 2003 -1104 с.
  13. Прокис Дж. Цифровая связь. Пер. с англ. / Под ред. Д. Д. Кловского. – М.: Радио и связь. 2000. – 800 с.
  14. Феер К. Беспроводная цифровая связь. Методы модуляции и расширения спектра: Пер. с англ. / Под ред. В.И. Журавлёва. – М.: Радио и связь, 2000. – 520 с.
  15. Диксон Р. К. Широкополосные системы: Пер. с англ. / Под ред. В. И. Журавлёва. – М.: Связь, 1979. – 304 с.
  16. Зюко А. Г., Кловский Д. Д., Назаров М. В., Финк Л. М. Теория передачи сигналов: Учебник для вузов. – М.: Связь, 1980. – 288 с.
  17. Волков Л. Н., Немировский М. С., Шинаков Ю. С. Система цифровой радиосвязи: базовые методы и характеристики: Учеб. пособие. – М.: Эко-Трендз, 2005. – 392 с.
  18. Бакулев П. А. Радиолокационные системы. Учебник для вузов. – М.: Радиотехника, 2004, 320 с.
  19. Белоцерковский Г. Б. Основы радиолокации и радиолокационные устройства. М., «Сов. радио», 1975. – 336 с.
  20. Варакин Л. Е. Системы связи с шумоподобными сигналами. – М.: Радио и связь, 1985. – 384 с.
  21. Обнаружение радиосигналов/П.С. Акимов, Ф. Ф. Евстрадов, С. И. Захаров и др.; Под ред. А. А. Колосова. – Радио и связь, 1989. – 288 с.
  22. Татарский Б. Г., Дудник П. И., Ильчук А. Р. Многофункциональные радиолокационные системы. Учебное пособие для вузов; под ред. Татарского Б. Г. – М.: Дрофа, 2007. – 283 с.
  23. Кук Ч., Берифельд М. Радиолокационные сигналы. Пер. с английского под ред. Кельзона В. С. М. Изд-во «Советское радио», 1971, 568 с.
  24. Борисов В. И. и др. Помехозащищённость систем радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки частоты. – М.: Радио и связь, 2000. – 384 с.
  25. Денисенко А. Н. Сигналы. Теоретическая радиотехника. Справочное пособие. – М.: Горячая линия – Телеком, 2005. – 704 с.
  26. Объединенная система распределения тактической информации JTIDS. /Клименко И.Н., Кисель В.В., Гончар А.Н.// Зарубежная радиоэлектроника. 1988. №5, С.85-96.
  27. Васин В. В., Степанов Б. М. – Справочник по радиолокации М.: «Сов радио», 1977, 320 с.
  28. Сигналы с расширением спектра в системах передачи информации. /Клименко И.Н., Кисель В.В., Земерин А.И.// Зарубежная радиоэлектроника. 1984, №11, С.45-59.
  29. Современное состояние и перспективы развития радиостанций зарубежных государств. /Харченко Н.К.//ЗВО-2003, №6 С.22-30.
  30. Тузов Г. И., Сивов В. А., Прытков В. И., Урядников Ю.Ф., Дергачев Ю. А., Сулиманов А. А. – Помехозащищенность радиосистем со сложными сигналами. – М.: Радио и связь, 1985. – 264 с.
  31. Пестряков В.Б., Афанасьев В. П., Гурвиц В. Л. - Шумоподобные сигналы в системах передачи информации. – Под ред.. проф.. В. Б. Пестрякова, М.: «Сов. Радио», 1973, 424 с.
  32. Борисов В. И., Зинчук В. М., Лимарев А. Е., Мухин Н. П., Нахамсон Г. С.; Под ред. В. И. Борисова. Помехозащищённость систем радиосвязи с расширением спектра сигналов модуляцией псевдослучайной последовательностью. – М.: Радио и связь, 2003. – 640 с.
  33. Харькевич А. А. – Борьба с помехами. – М.: «Наука», 1965. - 275с.
  34. Ширман Я. Д. и др. Теоретические основы радиолокации. Учебное пособие для вузов. М.: «Советское радио», 1970. – 560 с.
  35. Максимов М. В., Бобнёв М. П., Кривицкий Б. Х. и др. Защита от радиопомех. М.: «Сов. Радио», 1976. – 496 с.
  36. Окунев Ю.Б. Цифровая передача информации фазоманипулированными сигналами. – М.: Радио и связь. – 1991. – 226 с.
  37. Ширман Я. Д., Манжос В. Н. Теория и техника обработки радиолокационной информации на фоне помех. – М.: Радио и связь, 1981. – 416 с.
  38. Гантмахер В. Е., Быстров Н. Е., Чеботарев Д. В. Шумоподобные сигналы. Анализ, синтез, обработка. – СПб.: Наука и Техника, 2005. – 400 с.
  39. Френкс Л. Теория сигналов. Пер. с англ., под ред. Вакмана Д. Е. – М.: «Сов. радио», 1974. – 344 с.
  40. Финк Л. М. Сигналы, помехи, ошибки… Заметки о некоторых неожиданностях, парадоксах и заблуждениях в теории связи. – 2-е изд. – М.: Радио и связь, 1984. – 256 с.

Зауваження. На цей час випускна робота перебуває в стадії розробки, тому викладений матеріал може незначно відрізнятися від тексту, викладеного в пояснювальній записці. Більш докладну інформацію про дослідження j-кореляційного приймача виявлення можна отримати після грудня 2011 року від автора цієї роботи тільки з письмового дозволу наукового керівника.


ДонНТУ > Портал магістрів ДонНТУ | Резюме | Реферат | Біографія | Iндівідуальний розділ