ДонНТУ   Портал магістрів
   

РЕФЕРАТ ЗА ТЕМОЮ ВИПУСКНОЇ РОБОТИ

Зміст

1. Актуальність проблеми

Проаналізувавши статистичні дані за період з 1985 р. по 2012 р. про вихід з ладу трансформаторних підстанцій 110/10 кВ, які експлуатуються в Донбасівській енергосистемі, з'ясувалося, що у більшості випадків підстанції виходять з ладу з наступних причин:

  1. Випадкова поява короткого замикання(КЗ) на лінії, що відходить; відмова в спрацьовуванні вимикача КРП, відмова в спрацьовуванні ввідного вимикача 10 кВ, через які пройшов наскрізний аварійний струм, а ввідний вимикач 110 кВ не чутливий до КЗ, яке випадково з'являється на лінії, що відходить;
  2. Випадкова поява КЗ в приєднаннях до шин фідерів КРП; відмова в спрацьовуванні ввідного вимикача 10 кВ, відмова в спрацьовуванні ввідного вимикача 110 кВ, через які пройшов наскрізний аварійний струм, а максимальний струмовий захист(МТЗ) комутаційного апарату на лінії 110 кВ не чутлива до КЗ, яке випадково з'являється в приєднаннях до шин фідерів КРУ;
  3. Випадкова поява КЗ в трансформаторі 110/10 кВ; відмова в спрацьовуванні ввідного вимикача 110 кВ, відмова в спрацьовуванні МТЗ комутаційного апарату на лінії 110 кВ, через які пройшов наскрізний аварійний струм.

Завдання полягає в тому, а через скільки часу необхідно проводити діагностику системи відключення захисних комутаційних апаратів, щоб вірогідність збігу у просторі та часі трьох випадкових подій була величиною маловірогідна, тобто

При дотриманні цієї умови займань ізоляції на підстанції не буде.

2. Мета роботи

Визначити оптимальні з точки зору пожежної безпеки терміни діагностики систем відключення захисних комутаційних апаратів трансформаторної підстанції. Для цього необхідно вирішити наступні завдання:

  1. Отримати залежності вірогідності виходу з ладу в плині часу t підстанції 110/10 кВ від частоти появи КЗ на лінії, що відходить, в приєднаннях до шин 10 кВ або в трансформаторі підстанції, надійності систем відключення ввідних вимикачів 10 кВ і 110 кВ і термінів їх діагностики;
  2. Визначити середній час до першого виходу з ладу трансформаторної підстанції і дисперсію часу між аваріями.

3. Наукова новизна роботи

На основі регулярних однорідних марківських процесів з дискретним числом станів і безперервним часом розроблена математична модель, що пояснює процес виходу з ладу трансформаторної підстанції 110/10 кВ в плині часу t, що відрізняється від відомої тим, що враховується не лише частота появи небезпечних подій, але і їх тривалість.

4. Практична цінність роботи

Розроблена методика розрахунків, за допомогою якої можна визначати оптимальні з точки зору безпеки терміни діагностики системи відключення вимикачів, при яких вірогідність займання ізоляції на трансформаторній підстанції є величина маловірогідна.

5. Огляд нормативних документів в області пожежної безпеки

Згідно з [1] вірогідність пожеж у вузлі навантаження впродовж року має бути не вища, ніж H = 1·10-6. Це означає, що якби впродовж 1 року під наглядом знаходилося N = 1000000 трансформаторних підстанцій, то допускалася б одна пожежа (n = 1) за цей період часу.

Вірогідність пожеж впродовдж року при H·t < 0.1 можна визначити за допомогою формули:

Значить, для вирішення питання забезпечення пожежної безпеки трансформаторних підстанцій при їх експлуатації необхідно отримати залежність: вірогідність займання ізоляції на підстанції впродовж року від частоти появи КЗ на лінії, що відходить, в приєднаннях до шин 10 кВ або в трансформаторі і тривалості його існування, надійності системи відключення ввідних вимикачів 10 кВ і 110 кВ, а також інтервалів часу між діагностами систем відключення вимикачів θ1, θ2 і θ3 (рис. 1).

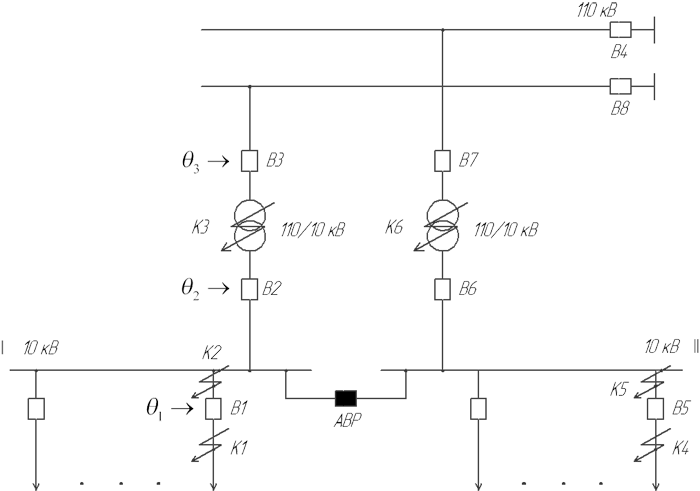
Схема електропостачання трансформаторної підстанції 110/10 кВ

Рисунок 1 – Схема електропостачання трансформаторної підстанції 110/10 кВ

За допомогою отриманої залежності можна буде вибирати такі інтервали часу між діагностиками систем відключення вимикачів θ1, θ2 і θ3, за яких вірогідність пожеж буде допустимою за нормативними документами [1].

6. Розробка математичної моделі, що описує процеси виходу з ладу трансформаторної підстанції

Введемо деякі поняття. Безпечним розумітимемо такий стан системи відключення вимикача, при якому у будь-який момент часу вона готова відключити КЗ, яке виникло в зоні дії її релейного захисту, а небезпечним - таке, при якому у разі появи КЗ на елементі, що захищається, відбувається відмова в системі спрацьовуванні захисного комутаційного апарату. Небезпечний стан системи відключення виявляються в результаті її діагностики: релейного захисту, приводу вимикача, контактної системи, дугогасительной камери і так далі.

Позначимо через ζk(t) процес зміни стану елементу (КЗ, відмова основного захисту, відмова резервного захисту), k = 1, 2, 3. Випадковий процес ζ1(t), ζ2(t) зміни стану комутаційних апаратів 1, 2 (2, 3; 3, 4) з часом може набувати двох значення: 0 - система відключення вимикача знаходиться в працездатному стані; 1 - система відключення знаходиться в відмовленному стані. Випадковий інтервал часу між появами КЗ на лінії, що відходить, в приєднаннях до шин 10 кВ або в трансформаторі і тривалістю його існування характеризуватимемо процесом ζ3(t).

Вірогідність переходів з безпечного стану в небезпечне за проміжок часу Δt дорівнює λkΔt+0(t), де 0(t) означає, що вірогідність появи більш одного небезпечного стану в інтервалі t+Δt є величиною маловірогідною у порівнянні з Δt. Вірогідність переходів з небезпечного стану в безпечний за проміжок часу Δt дорівнює μkΔt+0(t). Параметр λk характеризує інтенсивність або швидкість, з якою безпечні проміжки часу змінюються небезпечними а μk – частоту або швижкість зміни небезпечних проміжків часу на безпечні [2].

Вихід з ладу підстанції (займання ізоляції) настане в мить, коли усі три процеси ζk(t) знаходитимуться в стані 1, тобто коли ζ1(t)=ζ2(t)=ζ3(t)=1.

Випадковий час до першої пожежі позначимо через τ(0). Виразимо значення середнього часу до першої пожежі через параметри процесів θ1, θ2 і θ3.

Сукупність вказаних процесів розглянемо як регулярний однорідний марківський процес з вісьмома дискретними станами і безперервним часом. Поведінка в часі такої системи повністю визначається матрицею переходів Р, яка в нашому випадку має вигляд:

Середній час до першого виходу з ладу трансформаторної підстанції знайдемо з системи рівнянь [3]:

де N=1-Q, Q - фундаментальна матриця, яку отримуємо з матриці переходів за допомогою виключення поглинаючого стану (останнього рядка і останнього стовпця).

Вірогідність займання ізоляції трансформаторної підстанції впродовж часу t знайдемо, користуючись загальною системою рівнянь для регулярного однорідного дискретного марківського процесу з поглинаючим станом і безперервним часом [5]:

де – вектор-строка; – вектор-строка; , I – одинична матриця.

Дисперсія часу до першого займання ізоляції трансформаторної підстанції [4], тобто до першого переходу в поглинаючий стан:

де .

7. Оцінка пожежної безпеки трансформаторних підстанцій і розробка рекомендацій для її підвищення

Пожежна безпека трансформаторних підстанцій повинна забезпечуватися на рівні вимог ГОСТ 12.1.004.91 [4]. Для схеми (рис. 1), зобразимо дерево формування пожежі підстанції (рис. 2) і схему мінімальних перерізів (рис. 3).

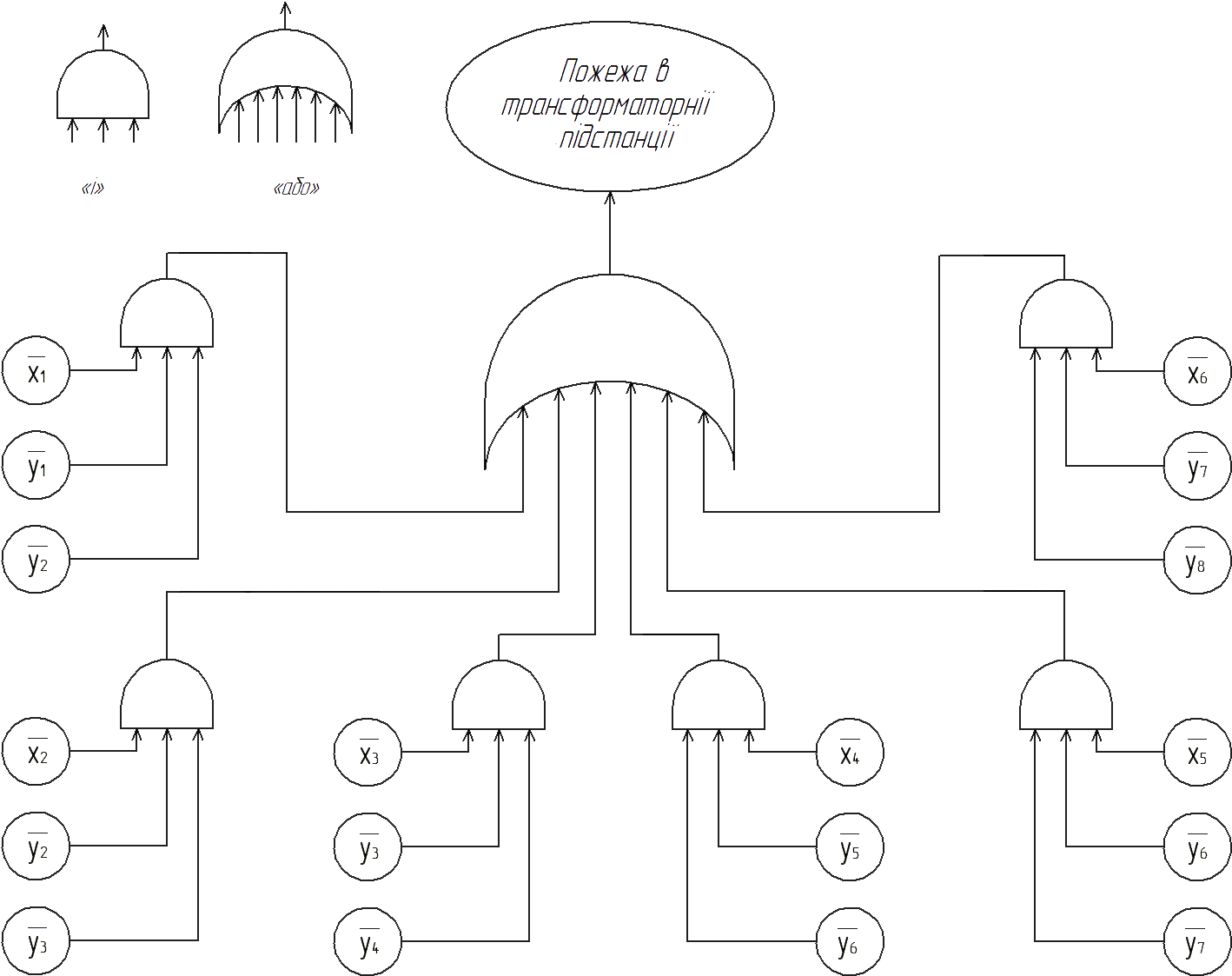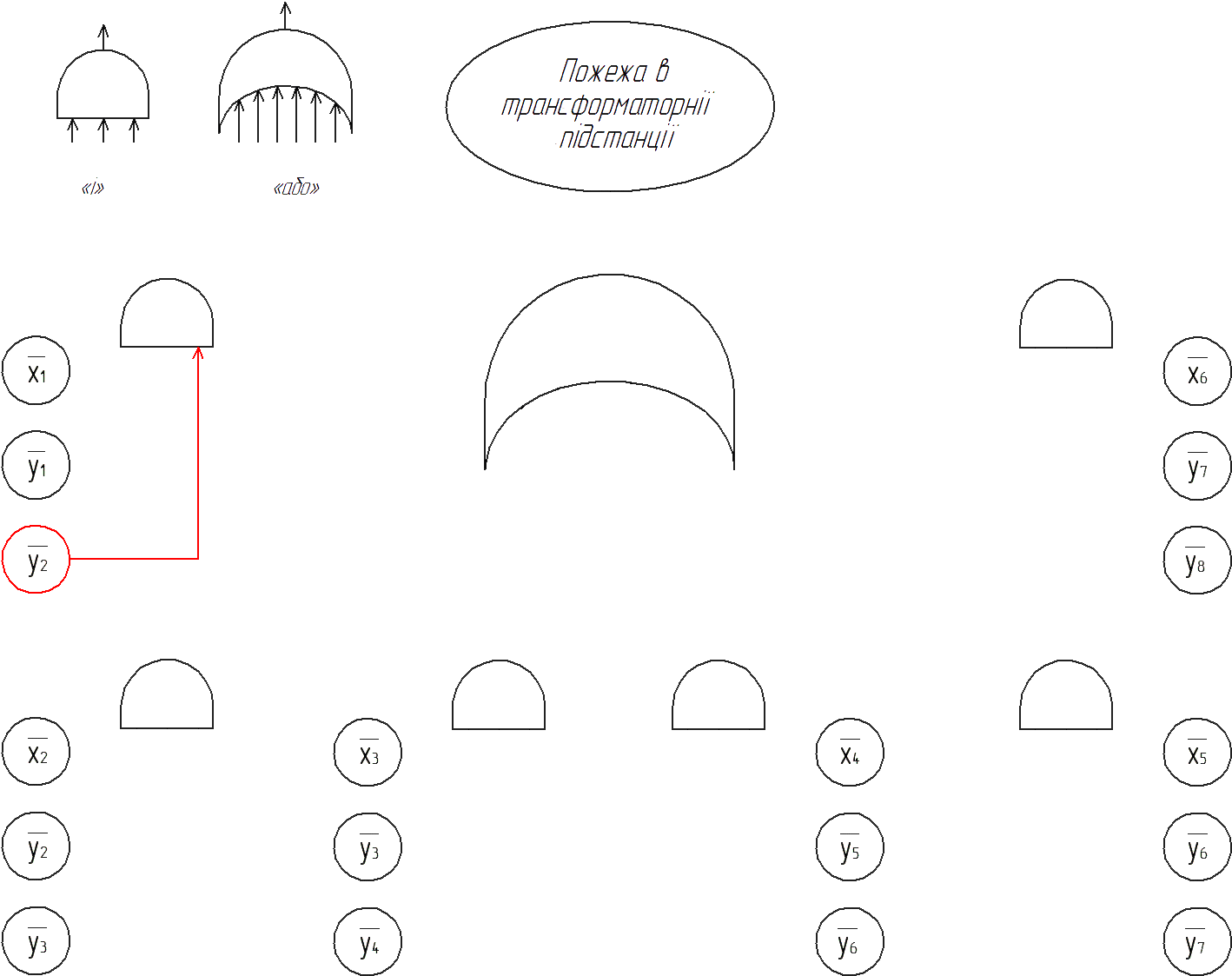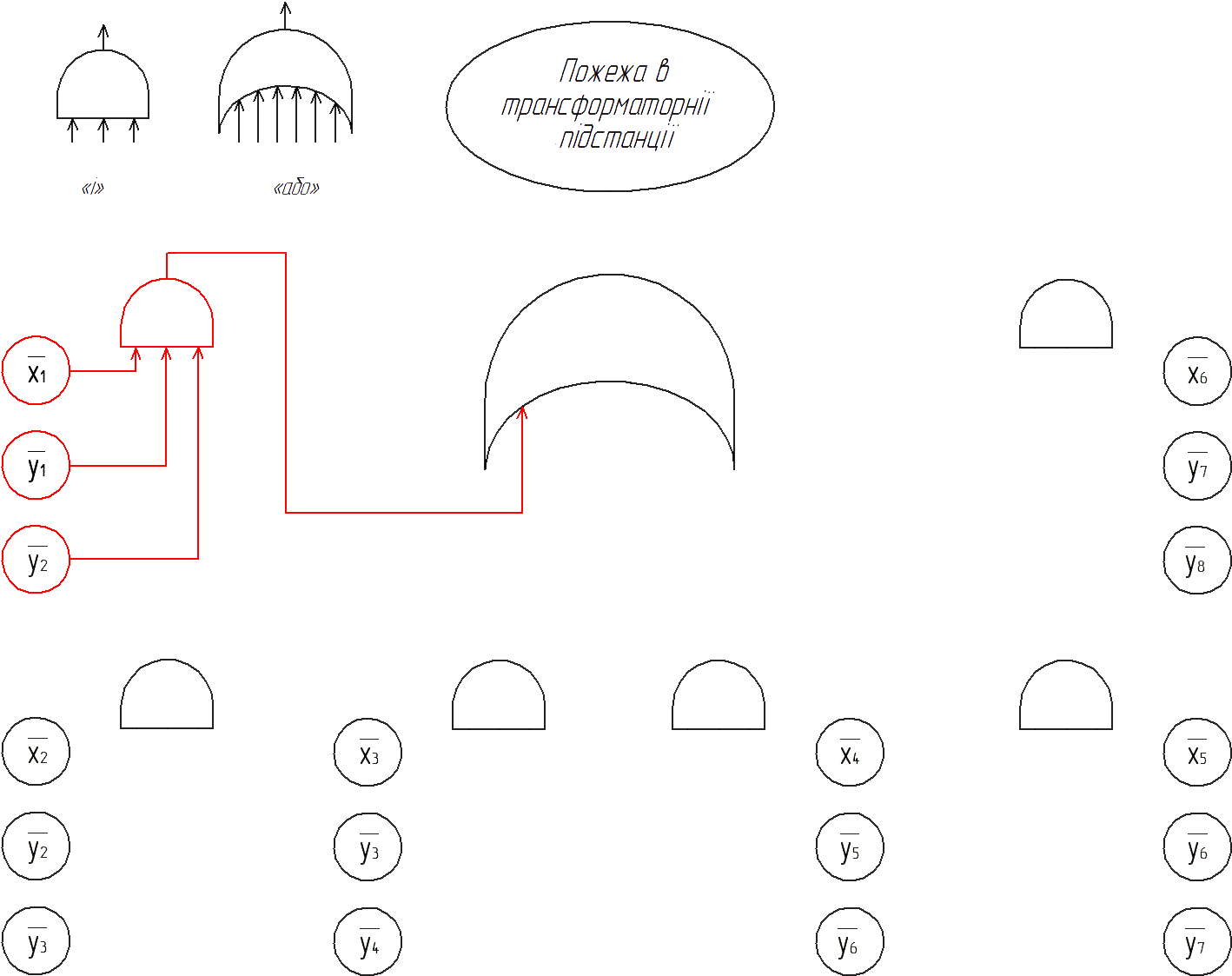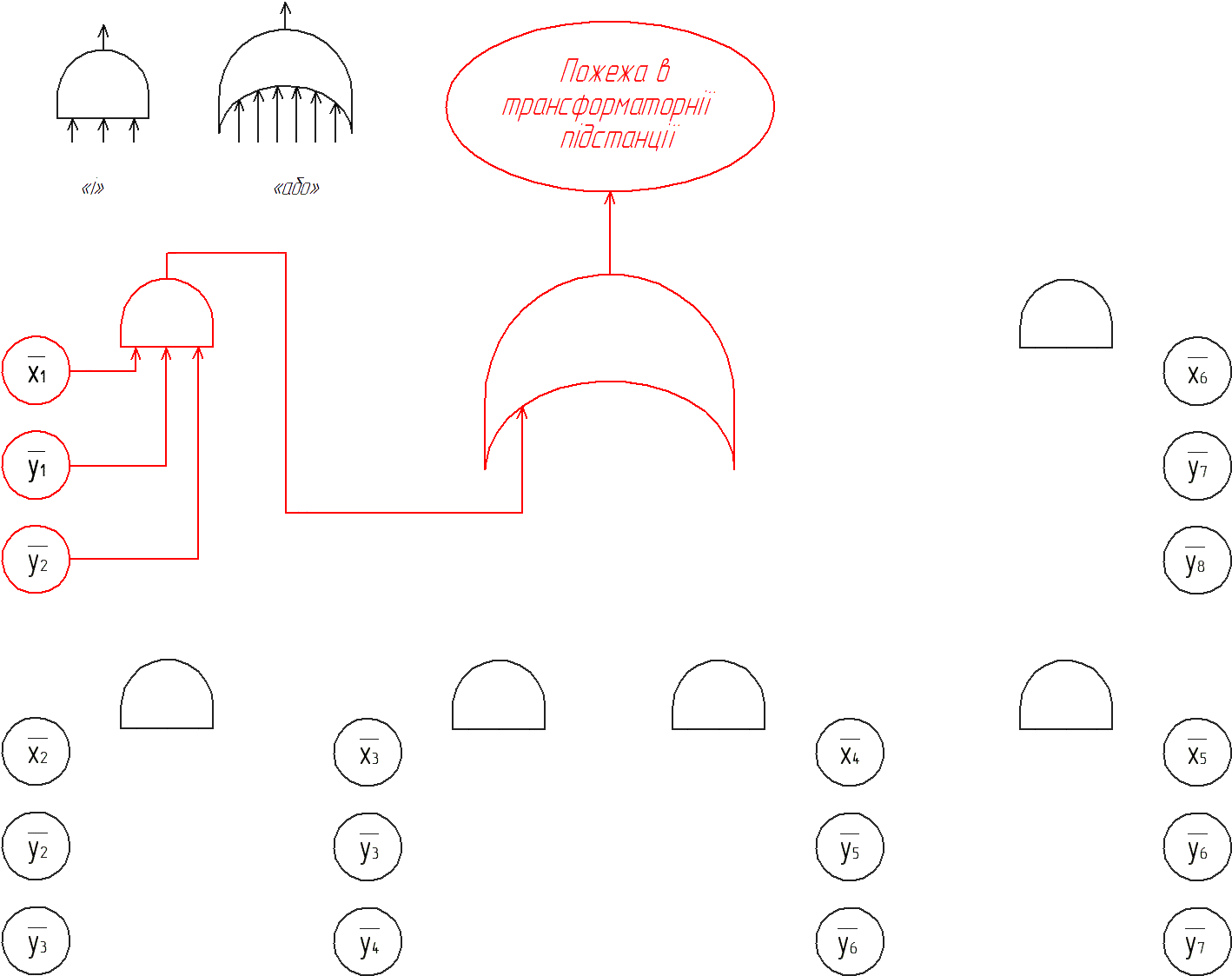
Дерево формування подій, збіг яких призводить до займання ізоляції(пожежа) і виходу з ладу підстанції

Рисунок 2 – Дерево формування подій, збіг яких призводить до займання ізоляції(пожежа) і виходу з ладу підстанції

где – відбулося КЗ; – сталася відмова в системі відключення i-того вимикача.

Схема мінімальних перерізів

Рисунок 3 – Схема мінімальних перерізів

Висновок

Отримана в магістерській роботі розрахункова формула і схеми мінімальних перерізів дозволяють оцінити пожежну безпеку трансформаторної підстанції будь-якого класу напруги і вибирати оптимальні з точки зору безпеки терміни діагностики систем відключення захисних комутаційних апаратів.

Список джерел

  1. Ковалев А.П. Оценка пожарной безопасности передвижных трансформаторных подстанций 110/35/6 кВ / А.П. Ковалев, А.В. Шевченко, И.В. Белоусенко // Промышленная энергетика. – 1991. – №6. – С. 28-31.
  2. Тихонов В.И. Марковские процессы / В.И. Тихонов, М.А. Миронов. – М.: Советское радио, 1977. – 488 с.
  3. Кемени Дж. Конечные цепи Маркова / Дж. Кемени, Дж. Сиел – М.: Наука, 1970. – 272 с.
  4. ГОСТ 12.1.004-91 ССБТ. Пожарная безопасность. Общие требования. – М.: Изд-во стандартов, 1991.
  5. Гнеденко Б.В. Математические методы в теории надежности / Б.В. Гнеденко, Ю.К. Беляев, А.Д. Соловьев – М.: Наука, 1965. – 524 с.
  6. Кельберт М.Я. Вероятность и статистика в примерах и задачах. Том 2. Марковские цепи как отправная точка теории случайных процессов и их приложения / М.Я. Кельберт, Ю.М. Сухов – М.: МЦНМО, 2009. – 586 с.
  7. Чжун Кай-лай Однородные цепи Маркова / Чжун Кай-лай Перев. с англ. – М.: Мир, 1964. – 426 с.
  8. Ковалев А.П. О проблемах оценки безопасности электротехнических объектов / А.П. Ковалев // Электричество. – 1991. – № 8. – С. 50-55.
  9. Лобанова И.С. Оценка пожарной безопасности передвижных подстанций – Автореферат [Электронный ресурс]. – Режим доступа: http://masters.donntu.ru/2008....