јвтор: G.A. Pugach1,2, A.A. Melnyk1,2, V.M. Khomenko1,3
1Donetsk National Technical University, 2Cergy-Pontoise University, 3Versailles St. Quentin-en-Yvelines University
Control of the ball-on-beam system using a simple PD controller optimized according to the maximum stable time criteria
јннотаци€
—истема Ђбалансир та шарї Ї нест≥йкою при в≥дсутност≥ ста-б≥л≥зуючих звТ€зк≥в. ¬ стат≥ розгл€нуто модель цього механ≥зму та системи управл≥нн€ ним. ћоделюванн€ виконано за допомогою про-грамного забезпеченн€ WebotsTM, при цьому прийн€то, що система Ї л≥н≥йною в зон≥ функц≥онуванн€. ќтриман≥ результати дозволили об-рати параметри системи стаб≥л≥зац≥њ, показали њњ ефективн≥сть.
1. Introduction
Nowadays, research in the field of robotics is strongly linked to simulation tools. On the one side the simulation helps to develop new advanced control algorithms and on the other side, it is always not feasible to build a certain robot system just to test some algorithms or it is not safe to perform tests on a real system. It has also an important role for off-line programming, to design mechanical structure of robots, robotic cells, etc. In this paper, an overview of the ball-on-beam system with simulations and the diversity of implementations are given. The scope of the paper is the control and simulation of a ball-on-beam electromechanical system.
The main capabilities of УWebotsФ simulation environment are: simulation of kinematics and dynamics of a system, integration of different sensor systems like vision or tactile sensors, scenarios for complex control tasks, visualization and integration of real systems in the simulation loop [1].
In the area of the controller design, there is a great variety of ap-proaches that can be used to stabilize a ball rolling on a beam: proportional-derivative (PD) [2], proportionalЦintegral-derivative controllers (PID) [3], linear quadratic regulator (LQR) [4] and Linear Quadratic Gaussian (LQG) [5] controller, robust control [6], sliding mode and variable structure control [7], fuzzy [8, 9] or neural networks [10] based control et al. The work [11] is used an approximated feedback linearization technics by dropping certain terms that leads to the singularities, because the relative degree of system is not well defined in certain singular point of the phase space. However, this approach does not work well when the system is away from the singularities, because of the approximation error that is generated by the dropped terms. A switching control law has been proposed in [12]: a controller that uses exact feedback linearization when the system is in the region far away from the singularities and a switch to the approximation feedback linearization controller when the system is approaching the singularities. A nonlinear tracking controller is known [13], which is based on approximate backstepping, and the simulation results show that this controller achieves better steady state error than other approximation methods. Other control approaches for the considered system includes a fuzzy controller [14, 15], interpolative [16], neural network [17] and a genetic controller [18]. Neural networks techniques [19] can control the balance of the system quite effectively using a population of feedforward neural network controllers that evolve towards an optimal controller through the use of a genetic algorithm. A hybrid approach employs linear control near the nominal condition [20] can be successfully used for control problem. In [21], a saturation control guaranteed global asymptotic stability was given. Another important study of system ball-on-beam is the use of vision systems in motion control applications. Apart from real-time constraints, the biggest problem that limits applications of a machine vision [22] system is its robustness to the noise present in the image as well as to the scene disturbances caused by background and foreground objects and to the non-ideal illumination conditions. To minimize this problem, a Kalman filter was implemented to predict the position of the ball [23].
Mathematical model
The situation at the individual link is quite complex but for the series of links the result can be written elegantly and concisely as a set of coupled differential equations in a standard matrix form [24]:

where Ц q, q, q respectively the vector of generalized joint coordinates, velocities and accelerations; M Цjoint-space inertia matrix; C Ц Coriolis and centripetal coupling matrix; F Цfriction force; G Цgravity loading; Q Цvector of generalized actuator forces associated with the generalized coordinates q; J Ц Jacobian.
The control law is described by the following equations:
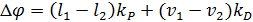

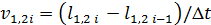
where Δφ Ц correction signal; l1, l2 Ц respectively the distance between the ball and the sensors 1 and 2; v1, v2 Ц velocity of the ball; kP Ц proportional coefficient; kD Ц differential coefficient; Δt Ц step of calculation.
Dynamic simulation of the ball-on-beam system
Based on the dynamic model of two revolute joints, this section investigates simulations of the ball-and-beam system (fig. 1).

Figure 1 - Webots model: 1) laser distance sensors; 2) metal ball, 32 grams; 3) active articulated support; 4) beam, 20 cm

Figure 2 - Results of the simulation: a) stabilization, b) external perturbations
Tuning of the PD controller coefficients kP and kD is realized in iterative optimization way. Criterion for choosing the optimum weight proportional is the maximum time (Tmax) to find the ball on beam.
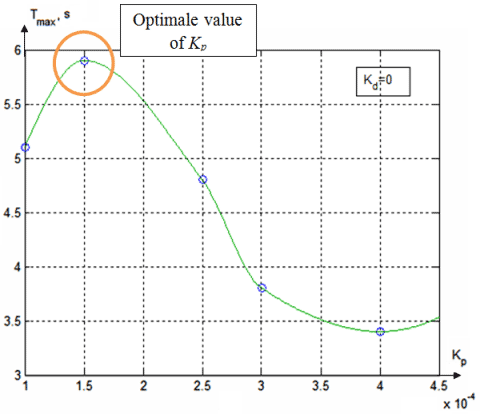
Figure 3 - Maximum duration (Tstab) of the ball staying on the beam as a function of kP
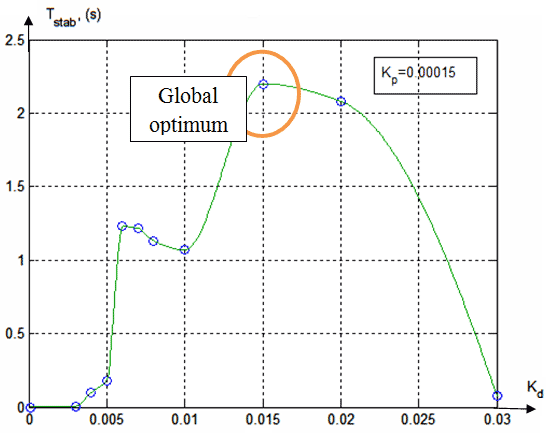
Figure 4 - Maximum duration (Tstab) of the ball staying on the beam as a function of kD
First, we determined the proportional coefficient (the value of the differential coefficient is set zero).
The maximum time to find the ball on beam as can be seen from figure 3 corresponds to kP = 0.00015. The results obtained by simulation are presented in figure 5. Then we found the value of kD, corresponding to kP = 0,00015. Selection criteria is the maximum time (Tstab) to which the ball will be in the stabilization.
The post-tuning results are presented on the figure 4, where we can see one local optimum (Tstab = 1,23, kD = 0,006) and the global optimum (Tstab = 2,2 au kD = 0,015). In the local optimum, the system behaves worse than in the global optimum.
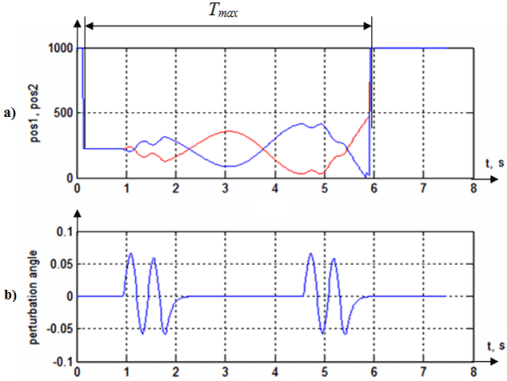
Figure 5 - Results of simulation (kP = 0,00015; kD = 0): a) Maximum duration (Tstab) of the ball stay-ing on the beam; b) external perturbations
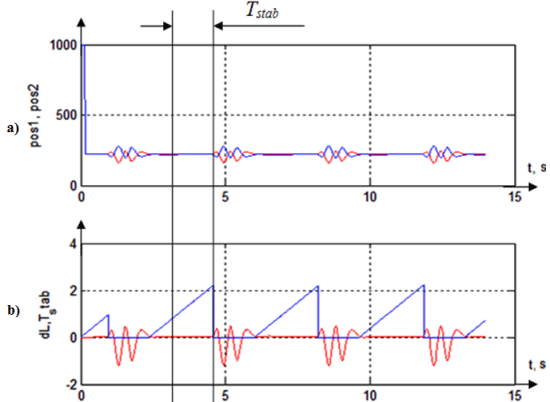
Figure 6 - Results of simulation for global optimum (kD = 0,015; kP = 0,00015): a) stabilizing pro-cess; b) shift of the ball from the center of the beam (dL) and the maximum duration (Tstab) of the ball staying on the beam
Second iteration of the algorithm of the PD controller coefficients optimization showed next results. It was initially supposed kD = 0,015 and the varied variable was kP. The obtained results (fig.7) showed that the difference between values of the local and global optimums does not exceed 5% (local optimum: Tstab = 2,15 for kP = 0,0004 and global optimal: Tstab = 2,27 for kP = 0,0001). Consequently, only two iterations are needed for the correct calculations of optimal values kP and kD.
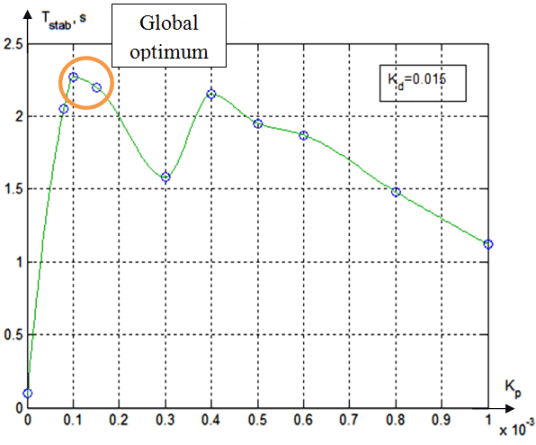
Figure 7 - Results debugging the coefficient kP (kD = 0,015)
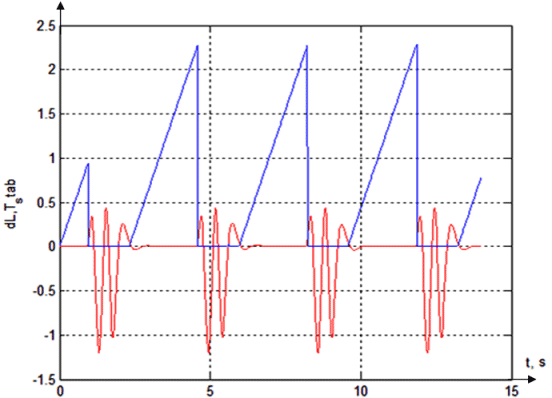
Figure 8 - Shift the ball from the center of the beam (dL) and the maximum time (Tstab) using op-timal values of kP and kD (kP = 0,0001; kD = 0,015)
Conclusion
The simulation is widely used for various technical and scientific problems. Actually, advanced systems require sophisticated simulation tools for accurate modeling of electromechanical articulated systems with the sufficient speed.
New challenges in the simulation of the systems are multi-body dy-namics that computes agent and object motions under influence of external forces, allows fast collision detection and contact determination, realistic visualization. The simulation tool Webots used for the design of the ball-on-beam system permitted us to test the proposed control algorithm. The optimal coefficients of a simple PD controller for the ball-on-beam system thus can be established within 2 iterations.
Further work envisages construction of the prototype of a ball-on-beam system and experimental tests.
Thanks to ETIS laboratory of the UCP University and LISV laboratory of the UVSQ University for providing us the material and discussing.
Bibliography
1. O. Michel. Webots: Professional Mobile Robot Simulation // International Journal of Advanced Robotic Systems. Ц Vol. 1, Num. 1, P. 39-42.
2. W. Yu. Nonlinear PD regulation for ball and beam system // International Journal of Electrical Engineering Education. Ц Vol. 46, No.1. Ц 2009. Ц P. 59-73.
3. B. Hamed. Application of a LabVIEW for Real-Time Control of Ball and Beam System // IACSIT International Journal of Engineering and Technology. Ц Vol.2, No.4. Ц 2010. Ц P. 401-407.
4. M.C. Lai, C.C. Chien, C.Y. Cheng, Z. Xu, Y.Mang. Nonlinear Tracking Control Via Approximate Backstepping // Proceedings of the American Control Conference, 1994. Ц Vol. 2. Ц 29 Jun-1 Jul. Ц 1994. ? P. 1339-1343.
5. A.E. Bryson, Y.G. Ho. Applied Optimal Control // N.Y: Hemisphere, 1975.
6. J. Huang, C.F. Lin. Robust nonlinear control of the ball and beam system // Pro-ceedings of the American Control Conference, 1995. Ц Vol. 1. Ц P. 306 Ц 310.
7. N. B. Almutairi, M. Zribi. On the sliding mode control of a Ball on a Beam system // Springer Tracts in Nonlinear Dynamics, 2009. Ц Vol. 59, Num. 1-2. Ц 2009. Ц P. 221-238.
8. Yi Guo, D.J. Hill, Zhong-Ping Jiang. Global nonlinear control of the ball and beam system // Proceedings of the 35th IEEE Conference on Decision and Control. Ц Vol. 3. Ц 11-13 Dec, 1996. Ц P. 2818-2823.
9. J. YI, N. Yubazaki, K. Hirota. Stabilization Control of Ball and Beam Systems // International Conference IFSA World Congress and 20th NAFIPS, 2001, Joint 9th Vol. 4. Ц P. 2229-2234.
10. P.H. Eaton, D. V. Prokhorov, D. C. Wunsch. Neurocontroller Alternatives for Fuzzy Ball and Beam Systems with Nonuniform Nonlinear Friction // IEEE Trans-actions of the Neural Networks, March 2000. Ц Vol. 11, No 2. Ц P. 423-435.
11. J. Hauser, S.Sastry, P. Kokotovic. Nonlinear control via approximate input-output linearization: the ball and beam example // IEEE Transactions on Automatic Con-trol.Ц Vol. 37. Ц Issue: 3. Ц March 1992. Ц P. 392-398.
12. C.J. Tomlin, S. Sastry, Switching through singularities // Proceedings of the 36th IEEE Conference on Decision and Control. Ц Vol. 1. Ц 1997. Ц P. 1-6.
13. M.C. Lai, C.C. Chien, C.Y. Cheng, Z. Xu, Y.Mang. Nonlinear Tracking Control Via Approximate Backstepping // Proceedings of the American Control Conference, 1994. Ц Vol. 2. Ц 29 Jun-1 Jul. Ц 1994. Ц P. 1339-1343.
14. Yi Guo, D.J. Hill, Zhong-Ping Jiang. Global nonlinear control of the ball and beam system // Proceedings of the 35th IEEE Conference on Decision and Control. Ц Vol. 3. Ц 11-13 Dec, 1996. Ц P. 2818-2823.
15. J. YI, N. Yubazaki, K. Hirota. Stabilization Control of Ball and Beam Systems // International Conference IFSA World Congress and 20th NAFIPS, 2001, Joint 9th Vol. 4. Ц P. 2229-2234.
16. S. Dale, T. L. Dragomir. Interpolative-type control solution for a Ball and Beam system // CEAI, Vol. 8, No. 3. Ц 2006. Ц P. 3-14.
17. P.H. Eaton, D. V. Prokhorov, D. C. Wunsch. Neurocontroller Alternatives for Fuzzy Ball and Beam Systems with Nonuniform Nonlinear Friction // IEEE Trans-actions of the Neural Networks, March 2000. Ц Vol. 11, No 2. Ц P. 423-435.
18. M.A. Marra, B.E. Boling, B.L. Walcott. Genetic control of a ball-beam system // Proceedings of the 1996 IEEE International Conference on Control Applications. Ц 1996. Ц P. 608-613.
19. C.J. Tomlin, S. Sastry, Switching through singularities // Proceedings of the 36th IEEE Conference on Decision and Control. Ц Vol. 1. Ц 1997. Ц P. 1-6.
20. A.T. Simmons, J. Y. Hung. Hybrid Control of Systems with Poorly Defined Rela-tive Degree: The Ball on Beam Example // 30th Annual Conference of IEEE Indus-trial Electronics Society, 2004. Ц Vol 3. Ц P. 2436-2440.
21. C. Barbu, R. Sepulchre, W. Lin and P.V. Kokotovic. Global Asymptotic Stabiliza-tion of the Ball-and-Beam System // Proceedings of the 36th IEEE Conference on Decision and Control. Ц 1997. Ц P. 2351-2355.
22. I. Petrovic, M. Brezak, R. Cupec. Machine vision based control of the ball and beam // 7th International Workshop Advanced Motion Control. Ц 2002. Ц P. 573-577.
23. S.A. Naz, R. Katebi, L. Balbis. Implementation of Kalman Filter on Ball And Beam Experiment Using Labview // International Conference Control 2006, 2006-08-30 - 2006-09-01, Glasgow.
24. P.Corke. Robotics, Vision and Control. Fundamental Algorithms in MATLAB // Springer Tracts in Advanced Robotics. Ц Vol. 73. Ц 2011. Ц P. 191-218.