Автор: E. Snegina1, A. Pougatch1, V. Khomenko1, 2, A. Melnyk1, 3, P. Henaff3, V. Borysenko1
1State Institution of Higher Education «Donetsk national technical university», 2University of Versailles Saint-Quentin-en-Yvelines, France, 3Cergy-Pontoise University, France
Practical aspects of Rowat-Selverston bio-inspired oscillator simulation
Abstract
The paper deals with practical aspects of the Rowat-Selverston biologically inspired oscillator simulated using modern research software. Most significant errors were estimated and their impact on the model of neuron dynamic behaviour was systematized. It permitted us to develop a rational high-performance simulation algorithm. The oscillator was implemented using C++ language and tested on a real-time system (industrial electronic unit controller BIA of a biped robot).
1. Introduction
Models of neural system were started to be used to resolve practical technical problems since 60-s of the XX century when the first “neuronal” electrical calculating machines were constructed. Their main difference is in the use of tuned ceil elements with weighed instead of a formal logic (AND, OR, NOT etc.) [1]. These elements are usually connected in a specified network called “neural network”. Perceptrons are a class of neural network corresponding to the acquisition and treatment of information in a feedforward scheme, this capacity is already well studied. Nowadays the interest of research is concentrated on the
The presented work is connected with an actual problem of modeling and simulation of central pattern generator neurons [2] that produce rhythmical movements observed in the living creatures. Using this way for movements production of humanoid robots should be the most natural when they interact with ambient environment or human. The input of a neuron is a current impulse that can start or stop oscillations of his membrane potential. Frequency and amplitude of oscillations, for a concrete organism, are determined by its chemical state that is achieved in technical systems by variation of model parameters. An idea of the work consists in the choice of appropriate methods of calculation of a Rowat-Selverston oscillator model [2, 3]. This one is a good approximation of a neuron that generates rhythmic movements in biological organisms. Different scientific software was applied that permitted to determine the most appropriate of them for the analysis of theoretic aspects of his dynamic behavior, and also for his practical realization (with robots ROBIAN biped [4] and KATANA-NEURONICS arm [5]).
The objective of this work is to compare several methods in the calculation of the Rowat-Selverston model according to the criteria of minimum calculation time, and the possibility of direct transition to its physical realization. The task considered the model calculation with different tools assuming the same parameters of a model was posed to achieve the formulated objective. Next tools were used: 1) continuous-time blocs of Simulink MATLAB; 2) scrip language of MATLAB; 3) programming language C++. The originality of received results consists in experimentally determined differences between simulation results of these different scientific calculation methods. Calculation errors were evaluated and reaction of the neuron model on the several typical inputs (impulse, step, sinus, meander) was established, that permitted to determine its dynamical properties.
In the first part of this article the mathematic model of a neuron is presented and activation curves are analyzed. The second part explains three principles of simulation of the model, one of them with practical application to a real biped robot [4]. Simulations show that maximum errors in phase and in absolute value of oscillations appear due to approximations of the model for real-time application. The final third part shoes different comportments of an oscillatory neuron.
Mathematic model of Rowat-Selverston oscillator
Biological neurons with several canals have complicated structure that creates difficulties in their modeling. American scientists Rowat and Selverston [2, 3] have presented (in 1997) an approximated model of such neuron. They took into account two groups of currents (“slow” and “fast”) and proposed two first order differential equations connecting currents and tensions [2]. The fast current is described by equation (1) and the slow – by equation (2):
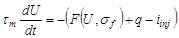
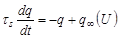
where τm << τs, τm is the neuron membrane time constant; τs is the time constant of a slow activation of currents; iinj is an injected current; U is a membrane tension; q is a slow current; U and q are variables; F(U, σf) is a nonlinear voltage-current characteristic of the fast current determined by the next equation [2]:

Function F(U, σf) is a fundamental part of a Rowat-Selverston model because, depending on the current gain σf, it determines different comportment of the oscillator [2, 3, 6, 7] (attenuating oscillations, aperiodic or oscillating without attenuation). Characteristics F(U, σf) can be linear when σf = 0, nonlinear bijective [8] when σf = 1, and nonlinear nonbijective when σf = 2 (fig. 1.a).
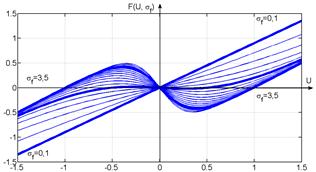
a)

b)
Figure 1 – Characteristics F(U, σf) for several values of: a) current gain σf, Af = 1; b) coefficient Af, σf = 3
Simulation procedure of an oscillating neuron
According to equations (1) and (2) a model was constructed in Simulink MATLAB (fig. 2) with formula (3) used to solve the fast part of the equation. Values of constants [2] are the next ones: Af = 1; σf = 3; τs = 1; τm = 1/20.
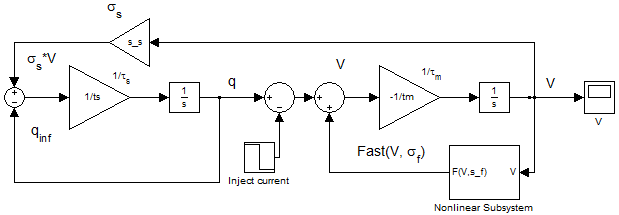
Figure 2 – Realization of a Rowat-Selverston oscillator in the Simulink environment
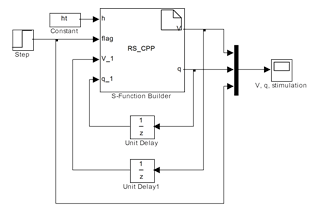
Figure 3 – Utilization of S-Function Builder block for debugging of the oscillator program rewritten on С++
The oscillator model description using Matlab script language was established. The numeric integration method ode45 with automatic step adaptation was used:
clc, clear all; close all; X0=[0;0];
interval=[0:0.001:10];
global flag
flag=1;
[T,X]=ode45('funcRS',interval,X0);
plot(T,X(:,1),':',T,X(:,2),'-'),grid on,legend('V','q'),xlabel('t, s')
function F=funcRS(t,x)
global flag
Af=1.0;tm=1/20;ts=10; ss=3;sf=1.6;
Iinj=funcIinj(flag); Es=0;
F=[-1/tm*(-Iinj+x(2)+(x(1)-Af*tanh(x(1)*sf/Af)));1/ts*(-x(2)+ss*(x(1)-Es))];
function O=funcIinj(flag)
if flag == 1, O = 1.6; else O = 0; end
For the С++ program debugging we used the SFunction Builder block (fig. 3). The neuron start signal was applied to its input (flag). Current and membrane potential were delayed for one period of sampling time. It is needed to solve numerically differential equations of a neuron (with firs order Euler method). The next program was optimized, that consists in usage of a table th function (100 points) and interpolation between neighbor points instead of a standard library function.
float i_inj, A_f, sig_f, E_s, sig_s, TM, TS,
u[101], th[101], u1, t, q_inf, i_fast, i;
u1=V_1[0]*sig_f/A_f;
if (flag[0] == 1), i_inj = 1.6;
else i_inj = 0;
A_f=1.0; sig_f=1.0;E_s=0.0;sig_s=3;
TM=1.0/20.0;TS=10.0;
if ((V_1[0]-E_s)>=0)
q_inf=sig_s*(V_1[0]-E_s);
else
q_inf=0.5*sig_s*(V_1[0]-E_s);
u[0]=-5.00;… th[0]=-0.99990920;…
for (i=0;i<=49;i++)
{ if (u1<=u[i]), break; }
if (i>=50)
for (i=100;i>=49;i--) { if (u1>=u[i]), break; }}
if (i==0), t=th[0];
else { if (i>=100), t=th[100];
else { if (i<50), t=(th[i]-th[i-1])*((u1-u[i-1])*10.0)+th[i-1];
else { if (i>=50), t=(th[i+1]-th[i])*((u1-u[i+1])*10.0)+th[i+1];}}}
i_fast=V_1[0]-A_f*t;
q[0]=q_1[0]+h[0]*((q_inf-q_1[0]))/TS; V[0]=V_1[0]+h[0]*(-(-i_inj+q_1[0]+i_fast))/TM;
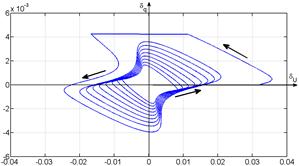
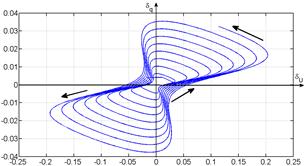
The simulation error using standard mathematic library functions (with double precision) and С++ program (with float precision, as processor modules of robots [4] and [5] are limited)
a)
b)
Figure 4 – Instantaneous errors analysis of the С++ neuron model: а) using functions of a hyperbolic tangent from a standard mathematic library (math.h); б) with linear interpolation of a hyperbolic tangent table function (100 points method)
The error of hyperbolic tangent approximation (using table function with interpolation between points) leads to a variable error in oscillation phase (for the considered case the first maximum of the error, equal to π radian, the maximum is reached at the time 589,5s, lineary rising with speed of 1,696·10-3 π/s, fig. 5). The corresponding graphic of an instantaneous error (fig. 4.b) diverges when the error increases. The root-mean-square error, practically, does not changes (0,231% for tension and 0,042% current).
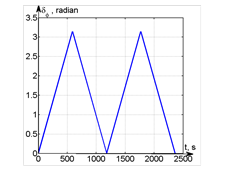
Figure 5 – Phase error characteristic using 100 points method hyperbolic tangent approximation
These results can be considered as acceptable because the influence of hyperbolic tangent approximation has mostly effect on the phase of generated oscillations (linear periodic phase drift), but not on their absolute values. Increase of a number of table points of th does not rational as it increases the time necessary to make calculations, moreover the maximum length of the data array in the memory of the industrial controller is limited. Nevertheless, usage of tables permits to liberate resources of the mathematical co-processor of the controller to resolve more complex problems of robot control (calculation of his geometric and dynamic models).
Analysis of the simulation results
Taking into account information presented above on the simulation precision, we study behaviors of the Rowat-Selverston oscillators from typical inputs. The model (fig. 2) was used. Results are presented in relative coordinates on (fig 6.a-d).

Figure 6 – Reaction of on oscillator on different inputs: а) impulse; б) step; в) sinus (T=0,5s); г) meander (T=0,5s).
The parameter Af influence mostly on the amplitude of oscillations for higher tensions U, so graphics (fig. 6.ab) are presented for several values of σf = {0,1; 1; 2} with fixed Af = 1; τs = 1; τm = 1/20.
Oscillations with different features were received: a) relaxation non-harmonic with frequency 1,11Hz for impulse input; b) aperiodic with constant time 0,25s for step input; c) quasi-harmonic periodic for sinusoidal input; d) nonharmonic periodic for meander input.
These simulation results showed characterize basic regimes of the Rowat-Selverston oscillator [3], present its ability to generate as periodical as and aperiodic signals. In this case synchronization with periodic input (sinus, meander) is not typical for biological systems, where “spiking” of neuron is controlled by discrete impulses of current (as shown on the fig. 5.a).
The considered simple model of the artificial oscillator does not take into account certain properties of its biological original – the neuron of a central pattern generator. For example, time delays that influent on the dynamics of a system; input signals actuate directly output of the oscillator. And, what is even more significant, one separate oscillator does not take into account synchronization function of a biological neuron, considered by most of researchers in the domain as principal. This phenomenon is used to generate rhythmic movements of anthropomorphic robots, as it represents a natural for a human procedure of interaction with its environment (gesticulation, periodic repeating actions etc.). However, there are publications justifying that the property of autosynchronization is intrinsic for a pair of Rowat- Selverston oscillators. This case is typical for biological systems, and will be a subject of our future researches.
Resume
1. Using of a table function of a hyperbolic tangent for a real-time realization of Rowat-Selverston oscillator almost does not influence on the root-mean-square error, but is manifested as a low frequency phase modulation of the oscillator output signal. 2. The most comfortable, between considered ways of simulation of the oscillator, is MATLAB Simulink; the highest speed of calculation is received for program written on С++. 3. As there are no operations of differentiation in the model, it is possible to use as double precision numbers, as and single precision.
Bibliography
1. Галушкин А.И. Теория нейронных сетей. Кн. 1.: Учеб. Пособие [для вузов] / Общая ред. А.И. Галушкина. – М.: ИПРЖР, 2000. – 416 с.: ил. (Нейрокомпьютеры и их применение). – ISBN 5-93108-05-8.
2. Rowat P.F. Oscillatory mechanisms in pairs of neurons connected with fast inhibitory synapses / Rowat P.F., Selverston A.I. // Journal of Computational Neuroscience 4. – Kluwer Academic Publishers, 1997. – 25 p.
3. Amrollah E. On the role of sensory feedbacks in Rowat–Selverston CPG to improve robot legged locomotion
/ E. Amrollah, P. Henaff // Frontiers Neurorobotics 4, 113, 2010. – 9 с.
4. Design and development of the biped prototype ROBIAN / [A. Konno, R. Sellaouti, F.B. Amar, F.B. Ouezdou] // Proceedings – IEEE International Conference on Robotics and Automation. – Vol. 2. – 2002. – pp. 1384-1389.
5. Katana 450 Benutzerhandbuch. Neuronics AG. – Document Nr: 233493. – Version 2.0.4. – 2001-2008.
6. Кузнецов А.П. Нелинейные колебания: Учеб. пособие для вузов / А.П. Кузнецов, С.П. Кузнецов, Н.М. Рыскин. – М.: Издательство физико-математической литературы, 2002. – 292 с.
7. Кириллов С.Ю. Исследование динамических режимов модели нейрона с последеполяризацией / С.Ю. Кириллов, В.В. Клиньшов // Труды научной конференции по радиофизике. – ННГУ, 2007. – 86 с.
8. Верещагин Н.К. Часть 1. Начала теории множеств. Лекции по математической логике и теории алгоритмов / Н.К. Верещагин, А. Шень. – [2-е изд., испр.] – М.: МЦНМО, 2002. – 128 с.