Relationship between viscosity and sugar concentration in aqueous sugar solution using the Stokes’ Law and Newton’s First Law of Motion
Автор: Evelyn Kim, The University of British Columbia Vancouver, Canada April 2010. Перевел Бей Сергей Викторович.
Аннотация
В этом эксперименте описывается взаимосвязь между вязкостью и концентрацией сахара в водном растворе путем расчета вязкости по закону Стокса и первому закону Ньютона. Вязкость и концентрация измерялись для 9 различных сахарных растворов по скорость падения шарика. Результат эксперимента показывает, что вязкость и концентрация сахарного раствора имеют две возможные зависимости: линейная η=1,19⋅концентр.+0,94 или экспоненциальная η=0,95⋅eконцентр.-0,006.
1. Введение
Вязкость является мерой силы трения (сопротивления) жидкости. Жидкости сопротивляются приложенной силе (или движению другого объекта) с разными скоростями движения каждого слоя. Кинематическая вязкость является мерой сопротивления жидкости под действием силы тяжести. Она обычно определяется с помощью капиллярного вискозиметра, принцип которого основан на измерении скорости протекания жидкости через капилляр.
С помощью многих экспериментов было доказано, что более вязкие жидкости движутся медленнее, чем менее вязкие [1]. Единица измерения СИ кинематической вязкости – см²⋅с-1, обычно измеряется в Сток (St). Кинематическая вязкость может быть преобразована в динамическую (Па⋅с и Н⋅м-2⋅с). В этом эксперименте вязкость жидкости будет измеряться с помощью скорости падения шарика вместо капиллярного вискозиметра.
Таким образом, следует применять первый закон Ньютона, который гласит, что если векторная сумма всех сил, действующих на объект, равна нулю, то ускорение объекта равно нулю, а его скорость постоянна. Шарик падает со скоростью свободного падения и замедляется после того, как на него действует выталкивающая сила. Кроме того, вязкость выступает в качестве силы трения в данном случае. Используя закон Стокса, вязкость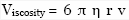 
, мы можем преобразовать уравнение. Таким образом, результирующая сила (сила тяжести) является векторной суммой всех возможных приложенных сил:
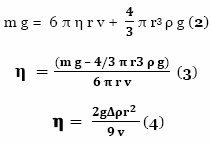
Эта гипотетическая формула показывает, что мы можем вычислить вязкость подстановкой переменных (m = масса шарика, g = 9.81 м²/с, r = радиус шарика, ρ = плотность жидкости, V = скорость падения шарика). В литературе сказано, что концентрация сахара зависит от вязкости экспоненциально [1]. Таким образом, в этом эксперименте взаимосвязь концентрации сахарных растворов и расчетной вязкости будет отображена на графиках как функция абсолютной вязкости от концентрации.
Исследование вязкости чистых жидкостей или водных растворов применяются во многих отраслях [2]. Например, взаимосвязь между концентрацией сахарного раствора и его вязкостью уже используется для определения концентрации сахара в нектарах цветов [1]. Поскольку вязкость нектаров влияет на другие организмы, которые участвуют в опылении, изучение концентрации сахара и вязкость может быть использовано в биологической области [1]. Кроме того, исследуемая нами проблема может быть также использована в пищевой промышленности [2].
2. Метод
2.1 Техника измерения
Формула (2) может быть использована для расчета вязкости жидкости, но для этого требуются данные по измерению плотности водного раствора, радиуса и массы шарика и время, за которое шарик преодолеет определенное расстояние в пределах жидкости. Прежде всего для расчета вязкости раствора с помощью скорости шарика необходимо найти конечные значения переменных. Таким образом, для вычисления плотности шара были измеряны его радиус и масса. Для каждого нового раствора с большей концентрацией в измерительный сосуд добавляли сахар.
Раствор разбавляли водой до общего объема 2 л. Этот шаг необходим для того, чтобы шарик попадал в жидкость на определенной высоте. Для проведения эксперимента раствор сахара был помещен в длинную трубку (Рис. 1). Измеряли высоту уровня раствора (h на рис. 1) и время, за которое шарик преодолел расстояние до дна сосуда (tf – ti на рис. 1). Эксперимент проводили 3 раза, чтоб вычислить среднее время падения. Для каждого испытания использовали новый сахарный раствор с различной концентрацией. Скоростью падения шарика и плотность жидкости были рассчитаны каждый раз.
2.2 Описание экспериментальной установки
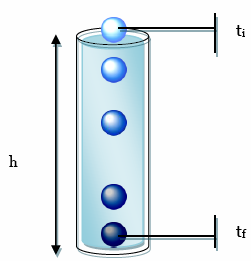
Рисунок 1. Описание экспериментальной установки
Описание экспериментальной установки: изначально шарик устанавливался прямо над жидкостью жидкость (в верхней части трубки). Время, за которое шарик преодолевал расстояние (tf – ti) измерялось в каждом испытании. Концентрация раствора каждый раз была разная (0M, 0.0400M, 0.0800M, 0.120M, 0.160M, 0.200M, 0.240M,0.280M и 0.320M). Высота (Н) измерялась с помощью линейки.
3. Результаты и обсуждение
3.1 Измерение
Таблица 1. Следующие данные были получены с помощью различных измерительных приборов, таких как подготовленной шкалы, линейки, а также таймера. Значения массы, длины и времени были округлены до половины цены деления.
Плотность сахарного раствора была рассчитана путем деления массы на объем, скорость падающего шарика – как расстояние, деленное на время. Все данные в таблице были использованы для расчета вязкости раствора по формуле.(4)
3.2 Погрешность расчета
Таблица 2. Погрешности измерений согласно п.2.
Погрешность была вычислена с помощью метода частных производных, который используется во многих лаборатория физики:
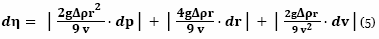
При измерении за такой короткий промежуток времени (менее чем за 1 секунду) невозможно получить точные данные. В общую погрешность вносят свой вклад средства измерения (подготовленные шкалы или мерный стакан), испарение сахарного раствора в ходе эксперимента, вследствие чего меняется значения плотности, а также неточность расчета вязкости по законам Стокса и Ньютона.
3.3 Графики
Таблица 3. Следующие данные были использованы для создания на графике ниже (рис. 2а и 2b). Данные в таблице были посчитаны с использованием таблицы 1. Погрешность вязкости была получена с помощью метода частных производных уравнения (5) и данных в таблице 2.
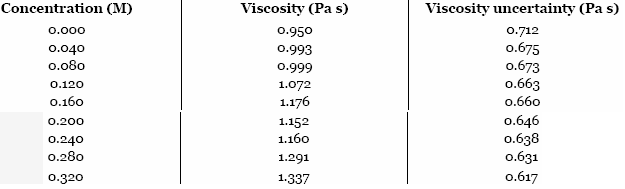
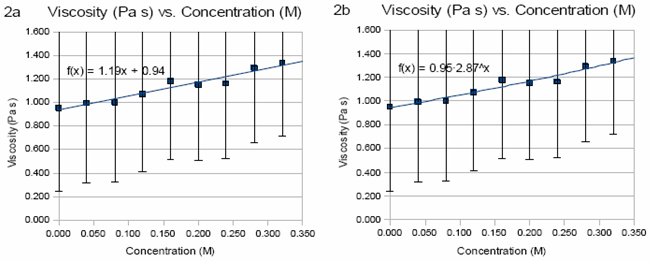
Рисунок 2. Зависимость вязкости от концентрации
Графики были построены на основе данных в таблице 3, где значения вязкости рассчитываются по формуле (4). Они отображают зависимость вязкости от концентрации. Погрешность вязкости вычисляется с помощью частной производной уравнения (5). Рисунок 2a отображает линейную зависимость вязкости от концентрации сахара η=1,19⋅концентр.+0,94. Рис 2б – экспоненциальный η=0,95⋅eконцентр.-0,006.
Таблица 4. Следующие данные используются для линеаризации рис. 2. Эта модель была создана для наблюдения прямо пропорциональной зависимости между вязкостью и концентрации сахарного раствора. Модель показывает, что при крутизне 0,95 начальная вязкость равна 0,944 Па⋅с.
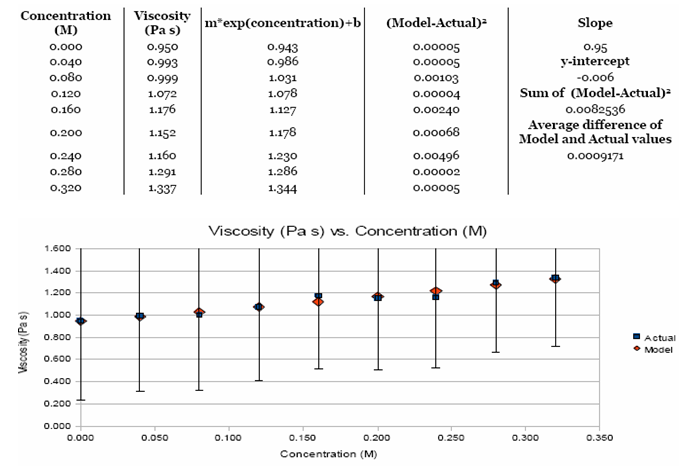
Рисунок 3. Сравнение фактических данных и значений модели уравнения
Модель η=0,95⋅eконцентр.-0,006 вычисляет близкие значения к измеренной вязкости. Все точки из модели укладываются в рамки погрешности и удовлетворяют требованиям других пунктов.
3.4 Анализ результатов
Согласно данным из таблицы 3 была рассчитана вязкость воды (η =950). В литературе [4] сказано, что вязкость воды варьируется от 1.002 до 0.8904. Так что можем сделать вывод о том, что приведенная модель выдает достаточно точный результат.
Затем для того, чтобы увидеть тенденцию изменения вязкости с изменением концентрации, построили график, на котором показали две зависимости: линейную и экспоненциальную (рис. 2a и 2b). Тем не менее, в исследовании нектара предположили, что вязкость возрастает экспоненциально с постоянным увеличением концентрации сахара [1]. Таким образом, для более точной интерпретации данных экспоненциальное значение измеряемой концентрации сахара рассчитаны и построены с концентрацией сахара и отображены на рисунке 3. На графике видно, что крутизна 0.95 и у-координата -0,006. Средняя погрешность модели равна 0,0009171. Такое малое значение означает, что модель можно считать "оптимальной" и что подходит для описания измеренного значения вязкости сахарного раствора. Моделирование показывает, что математическую связь между вязкостью и сахара концентрация водного раствора сахара можно описать экспоненциальной или линейной зависимостью. Другими словами, вязкость возрастает по экспоненте с увеличением концентрации сахара в растворе.
4. Заключение
На протяжении эксперимента мы рассмотрели две возможных зависимости между вязкостью и концентрации сахарного раствора: линейной и экспоненциальной. Таким образом, концентрация сахара в водном растворе сахара или вязкости раствора сахара при комнатной температуре может быть определена с помощью одного из двух метода. Однако дальнейшие исследования или проведение эксперимента над моделью концентрации сахара и его вязкости должно быть сделано с более точным оборудованием для того, чтобы подтвердить или определить, есть ли взаимосвязь двух переменных на самом деле в линейной (η=1,19⋅концентр.+0,94) или экспоненциальной (η=0,95⋅eконцентр.-0,006) зависимостях.
Список использованной литературы
1. Baker, H. G. 1 975. Sugar concentrations in nectars from hummingbird flowers. Biotropica. USA 7. 31-41. (1975).
2. Chirife, J. and Buera, M. P. A simple model for predicting the viscosity of sugar and ligosaccharide solutions. Journal of Food Engineering. USA 33, 221–226. (1997).
3. Vern Lindberg. "Uncertainties and Error Propagation". Uncertainties, Graphing, and the Vernier Caliper. Rochester Institute of Technology. pp. 1. Archived from the original on 2004-11-12. http://www.rit.edu/cos/uphysics/uncertainties/Uncertaintiespart2.html. USA Retrieved 2010-03-19. "The guiding principle in all cases is to consider the most pessimistic situation."
4. Weast, R. C. et al. (eds) CRC Handbook of Chemistry and Physics (Boca Raton, FL: CRC) USA (1990)