Study of the use of wavelet transforms to handle multimedia traffic
Content
- INTRODUCTION
- 1 OVERVIEW OF ALGORITHM
- 2 DEVELOPMENT IMAGE COMPRESSION ALGORITHM USING WAVELET - CHANGES
- 2.1 Selection of wavelet decomposition
- 3 ANALYSIS OF RESULTS OF THE ENCODER
- 3.1 Analysis of the quality of the reproduced image in the selected parameters
- 3.2 Analysis of the size of the compressed image
- CONCLUSIONS
- REFERENCES
INTRODUCTION
In today's world a person spends a lot of time with the computer. Data are becoming an integral part not only of successful job, but leisure as well. Most of this data comprise a variety of graphic images: work schedules, bar charts and personal photos. The task of modern technology is to ensure the safety of this information and provide quick access of the user to it. Take for example the following data: a modest, not a qualitative illustration on the cover of a book the size of 500x800 pixels, will take 1.2 Mb, and at the same time uncompressed color image size of 2000 x 1000 pixels has a size of about 6 megabytes. The size of the images obtained from professional cameras or scanners can be even greater. So it is necessary to compress images stored on the media and transferred of telecommunication channels. Image compression also has benefits for each of the existing industry. First, the image compression technique was most frequently used in the industry, which is engaged in printing, storing data and telecommunications. But now a form of digital image compression is applied in areas such as fax transmission, satellite remote sensing, high-definition television, etc. In addition, image compression is also useful for any organization that needs to view and save images being standardized. These organizations include state government agencies, museums, galleries, libraries, archives, and so on.
1 OVERVIEW OF ALGORITHMS
There are two main approaches to the construction of data compression algorithms: algorithms for lossless compression and loss compression algorithms. Lossless compression - a method of compression of video, audio, graphics, documents submitted in digital form. When using it, the encoded data can be recovered up to a bit. In this case the original data is completely recovered from the compressed state. For each type of digital information, there is its own optimal lossless compression algorithm. Lossless compression is used when the identity of the important original compressed data. Loss compression - the compression of data when uncompressed data differ from the original, but the degree of difference is not significant in terms of their future use. This type of compression is often used to compress audio and video, still images in the Internet, particularly in the stream data transmission and digital telephony.
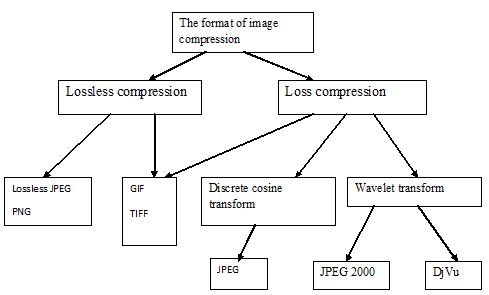
Figure 1.1 – Block diagram of the format of belonging to the algorithm.
While compressing the image there arises the question of how to compare the reconstructed image and the original. It is known that human eyesight and machine apparition are fundamentally different from each other. High machining (for machine) does not necessarily mean high quality (human) reproduction, because the human eye has a nonlinear behavior and subjectivity. That is why there are many metrics analyzing the image. For analysis the following metrics: PSNR, SSIM, MSE, Corr, as well as expert assessment of human vision were chosen.
Expert criteria of human eyesight.
This is a subjective criterion, but in some cases, the most effective one. Evaluation is done on a five-point principle. Score "excellent" receives the reconstructed image that dos not differ from the original. Score "good" received the restored image with a slight distortion, but they are only seen when comparing the original and the reproduced image. Score "satisfactory" receives an image having a little distortion. Score "unsatisfactory" receives an image having a significant distortion. Score "poor" receives an image that is difficult to identify.
2 DEVELOPMENT IMAGE COMPRESSION ALGORITHM USING WAVELET - TRANSFORMATION
As indicated in paragraph 1, the image has some redundant information. It can be removed from it so that the reconstructed image does not differ for the human eye. In this way image can be compressed. Therefore developed an algorithm that will focus on static images (color images that contain a lot of half-tones) are most commonly used in telecommunication networks. Any image can be represented by three two-dimensional matrixes containing the raw data for each layer of color (R, G, B). Then the general scheme of the encoder can be displayed:
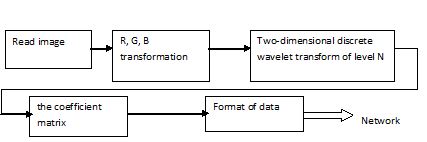
Figure 2.1 – The general scheme of the encoder.
2.1 Selection of wavelet decomposition
Now the choice of wavelets is large enough. Only in the package Wavelet Toolbox 2.0/2.1 has half dozen basic types of wavelets and a variety of options for a number of basic types of wavelets. However, the unjustified use of a particular type of wavelet may lead to errors. The algorithm that was described above can run on any wavelet that supports discrete two-dimensional analysis. Here is a graphic example of a decomposition of the image:

Figure 2.2 – Example of decomposition of the image to the fourth level Daubechies wavelet.
(Animation: 4 frame, 0.8 sec delay, size 118 Kb,endless loop, program – Easy GIF Animator)
The evaluation will be made on the vision criteria described in paragraph 1 and parameters Nzero and Ereg. Where Nzero - the number of zeros in the matrix coefficients of the image, and Ereg - the value of the recovered energy in the threshold value processing - "Remove near 0" - delete threshold value close to 0. These studies are summarized in table 2.1.
Table 2.1 – Results of a general analysis of wavelets.
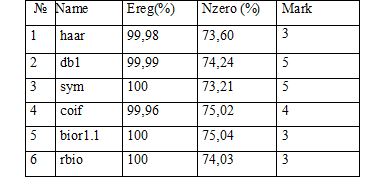
Based on the results shown in table 2.1, the Daubechies wavelet have been chosen and considered in more details. These studies are summarized in Table 2.2
Table 2.2 - Results of the analysis of Daubechies wavelets .
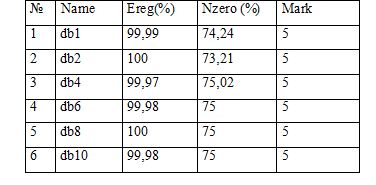
As the numbers of wavelets over 4 have almost identical results, the wavelet db4 as a wavelet with the largest number of zeros is chosen. The next step is to choose the number of levels of decomposition, which will be used for the chosen wavelet. These studies are summarized in table 2.3
Table 2.3 - Results of the analysis of the level of decomposition of Daubechies wavelets.
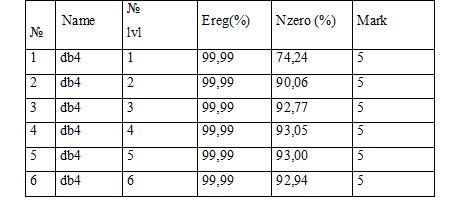
So the best will be the fourth level of decomposition of the image. Next, it should be decided which of the methods of search boundary treatment, which provides a development package MatLab, will be handling the expansion coefficients of the matrices. Processing will be conducted for each separate local level to achieve greater effect. These studies are summarized in table 2.4.
Table 2.4 – Results of the analysis process for the Daubechies 4 wavelet.
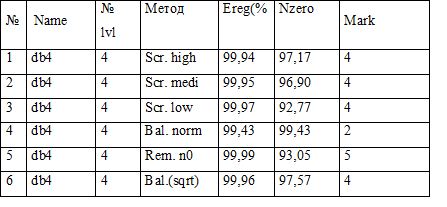
Based on these studies, a method of extracting value close to 0 (Rem. n0), as the highest quality of all the methods can be chosen.
3 ANALYSIS OF RESULTS OF THE ENCODER
Since the developed algorithm is focused only on full-color images, so a comparison of it with other algorithms, we focus only on the type of photographic color images, even if they are not optimal for a particular format.
3.1 Analysis of the of reproduced image quality in the selected parameters
In the previous sections we have chosen parameters of the encoder, which were designed to ensure the maximum number of zeros in the matrix of coefficients, so that the reconstructed image does not differ from the original human eyesight.
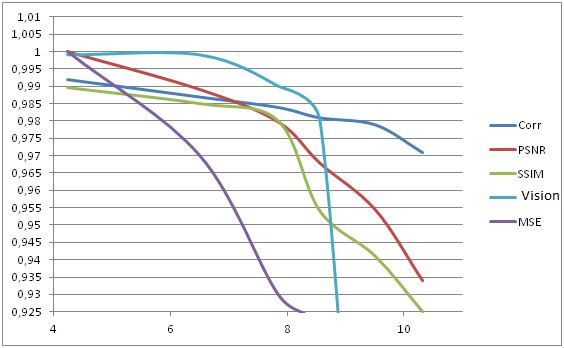
Figure 3.1 – Graph of the metric on the compression ratio.
Analyzing the results, we conclude that the most appropriate assessment criteria, which are similar to human sight, are the PSNR and SSIM criteria. MSE criterion, even at low compression ratio begins to decline rapidly, indicating a significant change in the image that is not a reality. A Corr criterion does not respond fast enough to reduction of image quality by increasing the compression ratio.
3.2 Analysis of the size of the compressed image
The main function of the algorithm is to compress images for transmission over a communication network. Therefore, we present the statistics for the most popular formats and own encoder for one image.
Table 3.1 - Statistical comparison
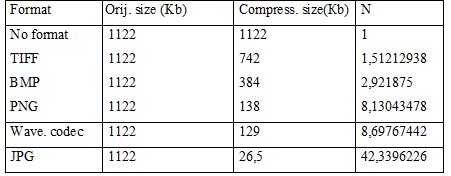
At this stage, a proprietary algorithm has more disadvantages than JPG, but it has not been implemented with some important algorithms, such as deleting the correlation of color layers and correlation of adjacent pixels in one layer. In order to make definitive conclusions about the algorithm it is necessary to take several images that are different color palette, the number of objects that have the same sizes and many color transitions. The results of compression should be compared with each other. Then the average compression rate for the encoder is: 8.4
CONCLUSIONS
In this paper the study methods and algorithms for image encoding is carried out. The first paragraph gives the main characteristics of modern algorithms (both lossy and lossless). There was selected the method of wavelet transforms, as the main method of study and development of a new algorithm in this research paper. The second paragraph gives us a preliminary model of encoding and decoding algorithms, defines all of the critical values, such as the type of mother wavelet, the number of levels of decomposition and the method for selecting the threshold for treatment. The third paragraph gives us the results of developed encoder and compares them with the results of today's popular formats.There are some inaccuracies in the encoders work. Their elimination will be the subject of future research.
REFERENCES
- Радионов И.В. "Использование вейвлет преобразований для обработки цветных цифровых изображений ". 58-ма НТК СП6ГУТ. 2005 р. –14с.
- Смоленцев Н.К. "Основы теории вейвлетов. Вейвлеты в MATLAB".М.ДМК Прес 2005 р.–304 с.
- Илюшкина Н., Чобану М. "Применение новых критериев оценки качества изображений после их сжатия" Современная электроника. №3 2007г. –4с.
- Ватолин Д.С. "Алгоритмы сжатия изображений" М. Методическое пособие." 1999г. -150с.
- Потемкин В.Г. "Система инженерных и научных расчетов MATLAB 5.x" – В 2-х т. Том 2. – М.: ДИАЛОГ-МИФИ, 1999 –336 с.
- Дьяконов В.Б. MATLAB. "Обработка сигналов и изображений. Специальный справочник." – С-Пб.: Питер, 2002. –608 с.
- Воробьев В.И.,Грибунини В.Г. "Теория и практика вейвлет - преобразования." – СПб.: Изд-во ВУС, 1999 –204 с.
- Добеши И. "Десять лекций по вейвлетам." – М.: Ижевск: РХД, 2001 –189 с.
