Дослідження застосування вейвлет-перетворень для обробки мультимедійного трафіку
Зміст
- ВСТУП
- ОГЛЯД ЛІТЕРАТУРНИХ ДЖЕРЕЛ
- 1 ОГЛЯД АЛГОРИТМІВ СТИСКУ
- 2 РОЗРОБКА АЛГОРИТМУ СТИСКУ ЗОБРАЖЕННЯ З ВИКОРИСТАННЯМ ВЕЙВЛЕТ - ПЕРЕТВОРЕНЬ
- 2.1 Вибір вейвлету для розкладу
- 3 АНАЛІЗ РЕЗУЛЬТАТІВ РОБОТИ КОДЕРУ
- 3.1 Аналіз якості відтвореного зображення за умов обраних параметрів
- 3.2 Аналіз розмірів стиснутого зображення
- ВИСНОВКИ
- ПЕРЕЛІК ПОСИЛАНЬ
ВСТУП
У сучасному світі людина велику кількість часу проводить за комп'ютером. Дані різного роду стають невід'ємною частиною як успішної роботи, так і домашнього відпочинку. Велику частину цих даних складають різні графічні зображення, починаючи від робочих графіків і гістограм і закінчуючи особистими фотографіями. І завдання сучасної техніки забезпечити зберігання цієї інформації і надавати швидкий доступ до неї користувачеві. Візьмемо для прикладу наступні дані: скромна, не дуже якісна ілюстрація на обкладинці книги розміром 500x800 пікселів, займе 1.2 Мб, а нестиснене повно кольорове зображення, розміром 2000 * 1000 пікселів матиме розмір близько 6 мегабайт. Розмір зображень, які отримують з професійних камер або сканерів високої роздільної здатності може бути ще більше. Але далеко не розміри зображення,що зберігаються на носіях, вплинули на розробку методів стиску зображення, а необхідність постійної роботи з ними і, найважливіше, передача по телекомунікаційних каналах. Стиснення зображень також має переваги для кожної існуючої на сьогоднішній день індустрії. Спочатку техніка стиснення зображень найбільш часто використовувалася в індустрії, що займається друком, збереженням даних і телекомунікаціями. Але в даний час цифрова форма стиснення зображень застосовується також у таких областях, як передача факсу, супутниковий дистанційний збір даних, телебачення підвищеної чіткості і т.п. Крім того, стиснення зображень також корисно для будь-якої організації, що вимагає, щоб перегляд і збереження зображень було стандартизовано. До таких організацій можна віднести державні урядові органи, музеї, галереї, бібліотеки, архіви тощо. Таким чином задача пошуку оптимального методу стиску зображень є дуже актуальною у наш час, адже це дозволить суттєво зменшити вимоги до пропускної здатності мереж та каналів зв’язку і збільшить можливості звичайного користувача, за умов обмеженої пропускної здатності, вдома.
ОГЛЯД ЛІТЕРАТУРНИХ ДЖЕРЕЛ
СтаттяИспользование вейвлет-преобразований для обработки цветных цифровых изображений
[1] Родіонова І.В. присвячена використанню вейвлет-перетворень для обробки зображень на системах з обмеженими ресурсами.
КнигаОсновы теории вейвлетов. Вейвлеты в MATLAB.
[2] автора Смоленцева Н.К. знайомить нас з різними математичними апаратами аналізу процесів, зосереджує увагу на теорії вейвлетів та їх реалізації у MatLab.
У статтіПрименение новых критериев оценки качества изображений после их сжатия
[3] автори Ілюшкина Н. , Чобану М., знайомлять нас з різними критеріями оцінки зображень після їх стиску, та аналізує переваги різних алгоритмів оцінки зображень.
Методичний посібникАлгоритмы сжатия изображений
[4] автора Ватолина Д.С. знайомить з основними алгоритмами стиску, базовими алгоритмами та напрямками розвитку теорії стиску.
У книзі Система инженерных и научных расчетов MATLAB 5.x
[5] надає повну інформацію для ведення інженерних розрахунків та візуалізацію результатів.
КнигаОбработка сигналов и изображений
[6] присвячена потужним засобам обробки сигналів та зображень,що їх надає MatLab.
У книзіТеория и практика вейвлет-преобразования.
[7] авторів Воробйова В.І. та Грибуніна В.Г. викладаються основні принципи вейвлет-перетворень.
У книзіДесять лекций по вейвлетам.
[8] Інгрід Добеши знайомить нас з цим математичним апаратом та використанням його для різноманітних задач. Це одна з найкращих книг для початку знайомства з цим математичним апаратом.
1 ОГЛЯД АЛГОРИТМІВ СТИСКУ
Основними особливостями, що дозволяють стискати зображення є те, що людський зір при аналізі зображення оперує контурами, загальним переходом кольорів і порівняно не чуттєвий до малих змін в зображенні. Таким чином, ми можемо створити ефективні алгоритми архівації зображень, в яких декомпресоване зображення не буде співпадати з оригіналом, однак людина цього не помітить. Дана особливість людського зору дозволила створити спеціальні алгоритми стиснення, орієнтовані тільки на зображення. Також легко помітити, що зображення, на відміну, наприклад, від тексту, має надмірність в 2-х вимірах. Тобто як правило, сусідні точки, як по горизонталі, так і по вертикалі, в зображенні близькі за кольором. Крім того, ми можемо використовувати подібність між шарами кольорової інтенсивності (зеленої, красної та голубої) в наших дослідженнях, що дає можливість створити ще більш ефективні алгоритми. Розрізняють 2 принципові підходи до побудови алгоритмів стиснення: алгоритми стиснення без втрат і алгоритми стиснення з втратами. Стиснення без втрат (англ. Lossless data compression) - метод стискання даних: відео, аудіо, графіки, документів, що представлені в цифровому вигляді, при використанні якого закодовані дані можуть бути відновлені з точністю до біта. При цьому оригінальні дані повністю відновлюються з стисненого стану. Для кожного з типів цифрової інформації, як правило, існують свої оптимальні алгоритми стиснення без втрат. Стиснення без втрат використовується, коли важлива ідентичність стислих даних оригіналу. Стиснення даних з втратами - метод стиску (компресії) даних, при використанні якого розпаковані дані відрізняються від вихідних, але ступінь відмінності не є істотною з точки зору їх подальшого використання. Цей тип компресії часто застосовується для стиснення аудіо-та відеоданих, статичних зображень, в Інтернеті, особливо в потоковій передачі даних і цифровій телефонії.
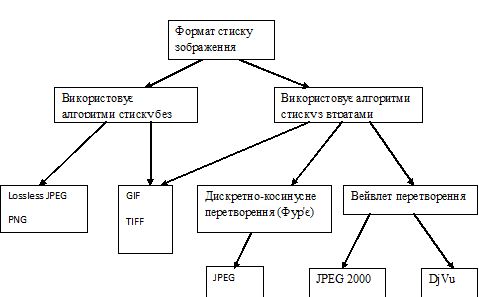
Рисунок 1.1 – Структурна схема належності формату до алгоритму.
При відтворенні стислих зображень виникає питання, як порівняти відтворене зображення та оригінал. Адже відомо, що людський зір та машинне бачення кардинально відрізняються одине від одного. Високі характеристики машинної обробки зовсім не означають високу якість відтворення для людини, тому що зір людини є нелінійний та суб’єктивний. Саме тому існує велика кількість метрик, що аналізують зображення. Для аналізу були обрані наступні метрики: PSNR, SSIM, MSE, Сorr, експертна оцінка людського зору.
Експертна оцінка людського зору.
Це є суб'єктивний, але у деяких випадках, найбільш ефективний критерій. Оцінка робиться за п’ятибальним принципом. Оцінку "відміно" отримує відтворене зображення, що не відрізняється від оригіналу. Оцінку "добре" отримує відтворене зображення, що має незначні спотворення, але вони помітні лише при порівнянні відтвореного зображення та оригіналу. Оцінку "задовільно" отримує зображення що має невеликі спотворення. Оцінку "незадовільно" отримує зображення, що має значні спотворення. Оцінку "погано" отримує зображення, що важко піддається ідентифікації.
Порівняння метрик ведеться на основі критерію оцінки людського зору. Дані виражаються у відносних одиницях та формують графіки залежності значення метрики від коефіцієнту стиску.
2 РОЗРОБКА АЛГОРИТМУ СТИСКУ ЗОБРАЖЕННЯ З ВИКОРИСТАННЯМ ВЕЙВЛЕТ - ПЕРЕТВОРЕНЬ
Як показано в пункті 1, зображення має надмірність інформації, яку для стиску можливо видалити з нього так, що відновлене зображення не буде відрізнятися нічим для зору людини. Тому алгоритм, що розроблюється, буде орієнтований на статичні зображення (кольорові зображення, що містять багато напівтонів), які найбільше використовуються у телекомунікаційних мережах.Будь-яке зображення може бути представлене як три двомірні матриці, що містять початкові дані для кожного шару кольору (R,G,B). Тоді загальну схему роботи кодеру відобразити так:
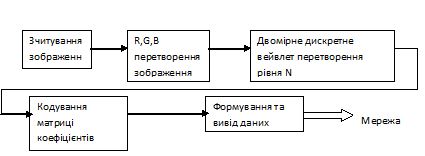
Рисунок 2.1 – Загальна схема кодеру.
2.1 Вибір вейвлету для розкладу
Зараз вибір вейвлетів досить великий. Тільки в пакеті Wavelet Toolbox 2.0/2.1 представлено півтора десятка базових типів вейвлетів і безліч варіантів для ряду базових типів вейвлетів. Однак, необґрунтоване застосування того або іншого типу вейвлету може привести до помилок. Такий вибір треба розглядати як перше наближення. Зрозуміло, при рішенні серйозних завдань в області обробки сигналів і зображень бажано застосувувати хоча б декількох типів вейвлетів з наступним порівнянням результатів і вибором найкращого з них. Алгоритм, що був описаний вище, може працювати на будь-яких вейвлетах, що підтримують дискретний двомірний розклад. Наведемо графічний приклад розкладу деякого зображення.

Рисунок 2.2 – Розклад зображення до четвертого рівня вейвлетом Добеши.
(Анімація: 4 кадри, 0.8 сек затримка, розмір 118 Кб, нескінченна кількість циклів, програма – Easy GIF Animator)
Оцінку відтворення зображення будемо здійснювати за критеріями відтворення, які були описані пункті 1нашої роботи та параметрами Nzero та Ereg. Де Nzero- кількість нулів у матрицях коефіцієнтів зображення, а Ereg - значення відновленої енергії при значенні порогої обробки -"Remove near 0"- порогу видалення значення, близького до 0. Данні дослідження зведемо до таблиці 2.1.
Таблиця 2.1 – Результати загального аналізу вейвлетів.
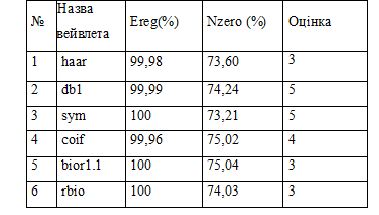
Виходячи з результатів таблиці 2.1 зупинимо свій вибір на вейвлетах Добеши та розглянемо їх більш детально. Данні дослідження зведемо до таблиці 2.2
Таблиця 2.2 – Результати аналізу вейвлетів Добеши .
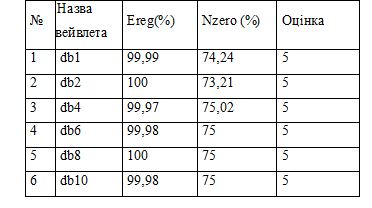
Отже номера вейвлетів після 4 мають майже однакові показники, тому оберемо вейвлет db4 - як вейвлет з найбільшою кількістю нулів.Наступним кроком ми повинні обрати кількість рівнів розкладання, що будуть використовуватися для обрано вейвлету. Данні дослідження зведемо до таблиці 2.3:
Таблиця 2.3 – Результати аналізу рівнів розкладання вейвлетів Добеши.
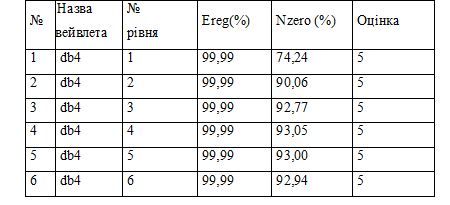
Отже оптимальним буде четвертий рівень розкладу зображення. Далі ми повинні обрати, за яким з методів пошуку граничної , які надає пакет розробки MatLab, буде відбуватись обробка коефіцієнтів матриць розкладання. Обробка буде проводитися для кожного локального рівня окремо для досягнення більшого ефекту. Данні дослідження зведемо до таблиці 2.4:
Таблиця 2.4 – Результати аналізу граничної обробки для вейвлету Добеши4 .
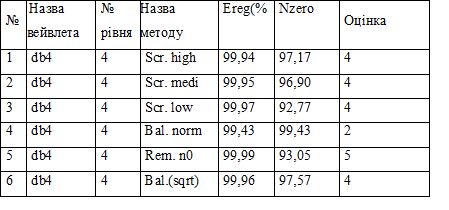
Виходячи з даних дослідження можливо обрати метод вилучення значення близького до 0(Rem. n0), як найбільш якісного з усіх методів.
3 АНАЛІЗ РЕЗУЛЬТАТІВ РОБОТИ КОДЕРУ
Оскільки розроблений алгоритм орієнтований тільки на повнокольорові зображення, тому при порівняні роботи його з іншими алгоритмами, будемо орієнтуватися лише на кольорові зображення фотографічного типу, навіть якщо вони не є оптимальними для якого-небудь формату.
3.1 Аналіз якості відтвореного зображення за умов обраних параметрів
У попередніх пунктах нами були обрані параметри кодеру, які повинні забезпечити максимальну кількість нулів у матрицях коефіцієнтів, так, щоб відтворене зображення не відрізнялось від оригіналу для зору людини. Проаналізуємо відтворене зображення методами експертної оцінки зору та різними метриками.
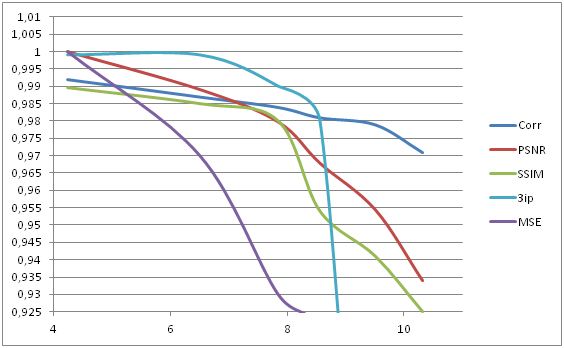
Рисунок 3.1 – Графік залежності метрики від коефіцієнту стиску .
Аналізуючи результати роботи, можливо дійти висновку, що найбільш адекватними крітеріями оцінки, графіки залежності яких нагадують графік залежності оцінки людського зору, є PSNR та SSIM крітерії. Крітерій MSЕ навіть при малих коефіцентах стиску починає стрімко спадати, вказуючи на значні зміни у зображенні, що не є дійсністю. А критерій Corr не достатньо швидко реагує на зниження якості зображення при збільшенні коефіціенту стиску. Таким чином при аналізі результатів роботи кодеру, що базується на вейвлет перетвореннях, можливо використання різноманітних метрик оцінки. Приоитетними серед них є метріки PSNR та SSIM, друга з яких є точнішою але більш сдладною та вимогає більших витрат при розраховуванні.
3.2 Аналіз розмірів стиснутого зображення
Основною функцією розробленого алгоритму є стискання зображення для передачі по мережі зв’язку. Тому наведемо статистичні дані для найбільш популярних форматів графічного відображення та власного кодеру для одного зображення .
Таблиця 3.1– Статистичні порівняння.
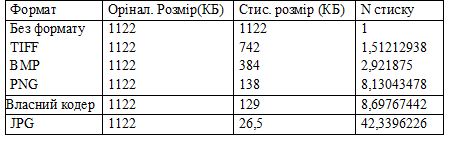
На даному етапі власний алгоритм програє формату JPG, але у ньому не були реалізовані деякі важливі властивості, такі як кореляція кольорових шарів та сусідніх пікселів у шарі. Щоб зробити остаточні висновки стосовно роботи алгоритму необхідно взяти декілька зображень, які будуть відрізнятися кольоровою палітрою, кількістю об’єктів, мати однакові розміри та багато кольорових переходів. Результати їх стиску порівняти між собою. Тоді середній коефіцієнт стиску для кодеру буде: 8,4. Такий коефіцієнт вищий за коефіцієнти стиску алгоритмів стиску без втрат, але не дуже великий, як коефіцієнт стиску для алгоритмів з втратами .
ВИСНОВКИ
У даній роботі проведене дослідження методів та алгоритмів кодування зображень. У першому пункті була дана характеристика сучасних головних алгоритмів (як з втратами, так і без втрат). Були визначені типові формати, які базуються на цих алгоритмах, а також був обраний метод вейвлет-перетворень, як головний метод для дослідження та побудови власного алгоритму у цій роботі. У другому пункті була надана попередня модель алгоритму кодування та декодування, визначені критичні для усієї роботи значення, такі, як тип материнського вейвлету, кількість рівнів розкладання та метод вибору порогу для обробки. У третьому пункті були надані результати роботи розробленого кодеру та порівняні з результатами роботи сучасних популярних форматів. Результати виявили деякі недоліки у розробленому кодері, але їх усунення та введення допоміжних алгоритмів кодування таких, як урахування кореляції кольорових шарів, стане предметом подальших досліджень.
ПЕРЕЛІК ПОСИЛАНЬ
- Родионов И.В. «Использование вейвлет-преобразований для обработки цветных цифровых изображений.» 58-ма НТК СП6ГУТ. 2005 р. –14с.
- Смоленцев Н.К. «Основы теории вейвлетов. Вейвлеты в MATLAB».М.ДМК Прес 2005 р.–304 с.
- Илюшкина Н. , Чобану М.«Применение новых критериев оценки качества изображений после их сжатия.» Современная электроника. №3 2007г. –4с.
- Ватолин Д.С. «Алгоритмы сжатия изображений.» М. Методическое пособие. 1999г. -150с.
- Потемкин В.Г. «Система инженерных и научных расчетов MATLAB 5.x.» – В 2-х т. Том 2. – М.: ДИАЛОГ-МИФИ, 1999 –336 с.
- Дьяконов В. MATLAB. «Обработка сигналов и изображений. Специальный справочник.» – С-Пб.: Питер, 2002. –608 с.
- Воробьев В.И., Грибунин В.Г. «Теория и практика вейвлет-преобразования.» – СПб.: Изд-во ВУС, 1999 –204 с.
- Добеши И. «Десять лекций по вейвлетам.» – М.: Ижевск: РХД, 2001 –189 с.
