Поток частиц и системы нечеткой логики в основе оптимального управления энергопотреблением асинхронного двигателя в нагрузочной схеме шахтного подъема
Аннотация
В работе исследуется важность контроллеров для энергосбережения при возможности частичной загрузки трехфазного асинхронного двигателя в шахтных подъемных установках. Входная мощность вектора контролируемого асинхронного двигателя мощностью 1 л. с. исследуется с помощью трех параметров, а именно: постоянного потока операции, модели потерь, используя оптимизацию случайным потоком (ОСП) и контроллер поиска в стационарных условиях. В этом исследовании считается, что уровень потока в машине регулируется таким образом, чтобы обеспечить минимальную потребляемую для заданного значения нагрузки на двигатель. Хотя поток параметров, задаваемый контроллером, повышает производительность двигателя в условиях минимальной мощности, они обусловливают скачки крутящего момента и скорости двигателя, таким образом снижает устойчивость. Чтобы повысить устойчивость привода при переменной скорости и нагрузке, была применена система, состоящая из устройства, работающего по нечеткому алгоритму, предварительно компенсирующего пропорционально-интегральный (НЧПИ) контроллер, а также сравнивают результаты его работы с выходными параметрами пропорционального интегрального (ПИ) контроллера. По результатам испытаний, данная система вместе с нечеткой логикой по эффективности превосходит обычные контроллеры и экономит 100 Вт мощности в тесте двигателя. В четырех тестовых ситуациях проверяется соответствие алгоритму ОСП. Для реализации ОСП используется C++.
Ключевые слова: оптимизации случайным потоком, нечеткая логика, асинхронный двигатель, минимизации потерь, шахтный подъем.
1. Вступление
Трехфазные асинхронные электродвигатели (АД) является наиболее часто используемыми в различных схемах электроприводов. Около 70% всей промышленной нагрузки приходится на асинхронные двигатели [1]. Цены на нефть, энергия которой преобразуется в электричество, а также на коммунальные услуги, зависящие от нефти и электричества, быстро растут. Таким образом, становится необходимым уделить основное внимание эффективности работы асинхронных двигателей [2]. Энергоемкие процессы стали объектом для исследования в целях снижения стоимости энергии и общей себестоимости энергии [3]. Как правило, асинхронные двигатели имеют высокий КПД при номинальной частоте вращения и крутящем моменте. Тем не менее, при малых нагрузках, потери в железе резко возрастают, что значительно снижает эффективность [4, 5]. Значения КПД и коэффициента мощности могут быть улучшены путем линейного наращивания возбуждения в зависимости от нагрузки. Для достижения этой цели можно изменить конструкцию асинхронного двигателя либо подавать питающее напряжение через инвертор [6]. То есть, магнитный поток должен быть уменьшен для получения баланса потерь между медью и железом [5]. В целом, существует три различных подхода к повышению эффективности асинхронного двигателя особенно в условиях малой нагрузки [4], а именно: контроллер модели потерь (КМП), контроллер поиска (КП) и таблицы поиска схемы. Многим исследователям были сообщены несколько стратегий с использованием различных переменных для минимизации потерь в АД. Некоторые алгоритмы используют скорости скольжения [4], [7], поток ротора [6], [8–10], мощность [8], [11], и напряжение [12]. Данная работа считает поток ротора в виде переменной и исследует ее оптимум посредством потерь модели в случае ОСП контроллера или прямой поиск в случае контроллера поиска. ОСП похож на генетические алгоритмы (ГА) тем, что система инициализируется при достаточном множестве случайных решений. Но, в отличие от ГА, каждое потенциальное решение также назначается в зависимости от скорости; такие потенциальные решения, называемые частицами, которые затем перелетали зону препятствий [13].
В связи с изменениями в потоке или в потоке, создающем ток для достижения минимальной мощности, система обладает низкой устойчивостью в условиях пульсации крутящего момента и скорости двигателя. НЧПИ-контроллер используется в данной работе для улучшения стабильности привода, когда оптимальный контроллер энергии активируется. Блок-схема предлагаемого контроллера показана на рис. 1. Крутящий момент производящий ток, сгенерированный ПИ-регулятором потока, и поток, производящий ток, сгенерированный контроллером мощности, превращаются в трехфазный ток. ШИМ-контроллер тока генерирует импульсы для запуска схемы преобразователя по величине ошибки, равной разности исходных значений токов и фактических величин. Организация этой работы заключается в следующем. В разделе 2 кратко описывалась диаграмма нагрузки шахтного подъема, раздел 3 посвящен обзору методов оптимизации эффективности, в разделе 4 получили потери в модели АД. В разделе 5 кратко приводится обсуждение алгоритма ОСП и его целевой функции, раздел 6 объясняет принцип работы НЧПИ-контроллера, в разделе 7 представлены результаты моделирования двигателя мощностью 1 л.с. Приводится анализ работы двигателя в оптимальном режиме с концентрацией энергии и скорости, и раздел 8 проверяет ОСП алгоритм с помощью четырех стандартных задач теста.
2. Диаграмма нагрузки шахтной подъемной установки
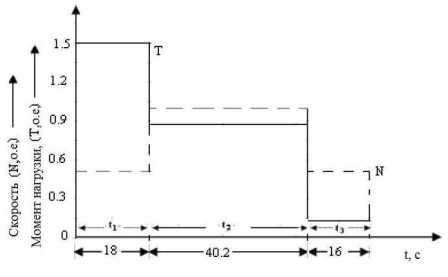
Для того чтобы проиллюстрировать важность эффективного контроля производственных процессов, считают нагрузку в реальной схеме шахтных подъемных установок в горнодобывающей промышленности (рис. 2) [14]. Двигатель мощностью, 2000 л.с., работает с переменной нагрузкой и скоростью, как показано на рис. 2. t3' – область нагрузки, где двигатель работает на малых нагрузках (0,14 о. е.) и половину номинальной скорости двигателя. В настоящем исследовании авторы полагают, что энергии оптимального управления в основном сосредоточены в этом регионе, так как регулировка уровня потока в основном требуется на легконагруженном состоянии [4–12], [15].
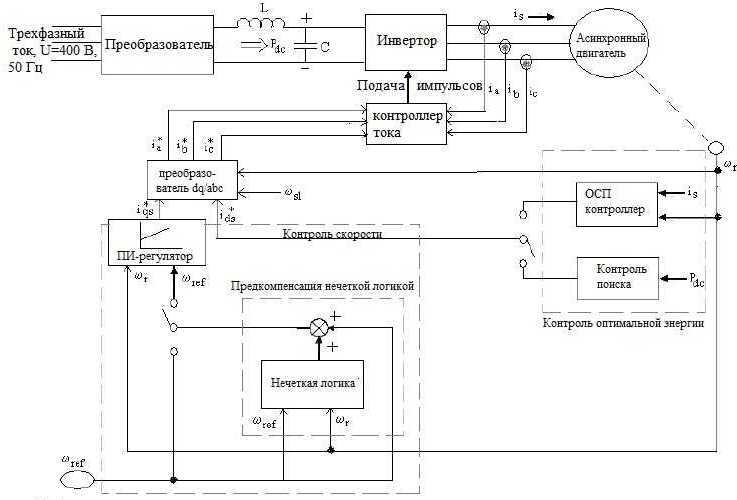
Рисунок 1 – Схема контроля оптиамального энергопотребления и сокрости на основе ОСП и нечеткой логики
Рисунок 2 – Нагрузочная диаграмма подъемной установки
3. Методы оптимизации эффективности
Асинхронный двигатель должен работать при номинальном потоке и номинальном значении момента нагрузки, где в качестве нагрузки крутящий момент меньше, чем номинальный, что приводит к снижению магнитных потерь в железе и тока намагничивания. При низких значениях нагрузки (до 15% от номинальной величины) работа по энергосбережению может уменьшить потери мощности еще на 70–90% [16]. В этом разделе обсуждаются различные типы контроллеров, которые используются для работы двигателя с меньшими затратами энергии, работающих на частичной нагрузке. Они заключаются в следующем.
3.1 Эксплуатация двигателя в
режиме звезда
Асинхронные двигатели работают
при малой нагрузке, требуя меньше крутящего момента. Подключение
двигателя по схеме Звезда
позволило в результате
снизить энергопотребление. Когда двигатель работает в режиме
звезда
,
напряжение применительно к обмотке статора фазы уменьшается.
Поскольку крутящий момент, развиваемый в двигателе, прямо
пропорционален квадрату напряжения, развиваемый крутящий момент в
режиме звезда
уменьшается в квадратный корень из трех раз. Таким
образом, двигатель может работать в режиме
звезды
до 0,33 о. е.
нагрузки. В этом случае крутящий момент на валу должен быть измерен и
найдены обоснованные значения параметров для управления подключенными
системами, а также необходимо измерять температуру для контроля работы
двигателя в пределах нормы. Этот метод не подходит для широкого спектра
режимов частичных нагрузок. Этот контроллер не имеет функции
преобразователя потерь в связи с отсутствием мощных электронных схем.
3.2 Контроль переменного напряжения фиксированной частоты (КПФЧ)
Вместо старта работы асинхронных двигателей на полном напряжении для плавного пуска может быть использован плавный старт на низких пусковых токах. Работа устройства плавного пуска заключается в постепенном линейном увеличении напряжения на двигателе, что дает возможность пуска двигателя. Контроллер трехфазного напряжения, который используется состоит из двух тиристоров на фазу в противовключении при параллельном соединении, где вход подключен к соответствующей фазе сетевого напряжения и выход – к каждой фазе двигателя. Устройство плавного пуска служит для применения пониженного напряжения для запуска двигателя и снижения напряжения на его зажимах при малой нагрузке. В этом случае потери железа снижаются, чем достигается энергосбережение.
3.3 Постоянное соотношение U/F управления
Постоянные U/F управления скалярным (переменные контролируются только по величине). Такой тип управления показан на рисунке 3 (а), реализация которого проста и низкая по стоимости. Оптимальная производительность двигателя может быть достигнута путем изменения напряжения и частоты (с сохранением постоянного значения их соотношения для поддержания максимального крутящего момента) с минимальными потерями. Целесообразно, создать контур управления скоростью, что в основном используется в насосных и вентиляторных установках.
3.4 Управление ориентировкой векторного поля
При контроле вектора переменные контролируются по величине и фазе. Этот метод контроля нуждается в большем количестве вычислений, чем стандартная схема U/F-управления [17]. В этом способе контроля асинхронный двигатель может быть смоделирован как двигатель постоянного тока после проведения простых преобразований. Поле, чью ориентацию генерирует контроллер, создает необходимые токи для управления двигателем. Эти токи создаются на основе эталонного крутящего момента.
3.5 Управление коэффициентом мощности
Если значения скольжения различны в асинхронном двигателе, импеданс двигателя и, следовательно, коэффициент мощности, тока и эффективность изменяются. Когда значение постоянного оптимального скольжения поддерживается с помощью контроллера напряжения, значение сопротивления по времени и, следовательно, коэффициент мощности и КПД остаются неизменными и оптимальными независимо от нагрузки [18]. Хотя контроль значения коэффициента мощности так прост для реализации, потому что не требует информации о скорости, что действительно только для одного конкретного двигателя [19].

Рисунок 3 – Оптимизационные контроллеры: а) контроль соотношения U/f, б) модель потерь, в) контроллер поиска
3.6 Управление частотой скольжения ротора
В этом режиме контроля оптимальная частота скольжения ротора рассчитана на широкий диапазон оборотов и крутящий момент данного двигателя и сведены в справочную таблицу. Целевая функция, которая показана, может соответствовать максимальному коэффициенту мощности и КПД. Оптимальное скольжение можно рассчитать с помощью эквивалентных параметров схемы асинхронного двигателя. Так как на выходе преобразователя напряжения питания появляются напряжения высших гармоник, расчет оптимального скольжения не может быть точным. Оптимальная частота скольжения может быть вычислена из измерения потребляемой мощности, мощности двигателя, преобразователя частоты и частоты скольжения [20]. Стохастические алгоритмы могут быть использованы для поиска оптимального значения скольжения в течение короткого срока. Ни в коем случае ограничения (линии тока и потока) не должны превышать номинальных значений.
3.7 Контроллер потерь модели
Контроллер потерь модели, показанной на рис. 3 (б), измеряет скорость и ток статора и через модель потери двигателя определяет оптимальный воздушный зазор потока [8]. Основная проблема такого подхода заключается в том, что метод требует точных значений параметров машины, которые включают основные потери и основной поток насыщения индуктивности [4]. Внутренняя часть алгоритма управления может быть в скалярной или векторной форме. Стохастические методы, как ОСП или генетический алгоритм могут быть использованы для поиска оптимального уровня потока от потери модели двигателя.
3.8 Контроллер поиска минимальной мощности
Этот контроллер измеряет мощность привода через определенные промежутки времени и ищет значение потока в результате чего достигается минимальная потребляемая мощность при заданных значениях скорости и момента показано на рисунке 3 (в). Этот метод является медленным для достижения оптимального значения, и пульсация крутящего момента в стационарном состоянии присутствует всегда [4].
4. Модель потери асинхронного дигателя
Схемы замещения асинхронного
двигателя аналогичны для трансформатора, его также называют
вращающийся трансформатор
.
При этом параметры
асинхронного двигателя являются производными от параметров для режима
холостого хода неподвижного ротора и могут быть легко выражены.
Схемы статора и ротора могут быть объединены путем корректировки
значений компонентов ротора в соответствии с действующим коэффициентом
трансформации трансформатора [21].
В этой
статье рассматриваются скалярные потери модели асинхронного двигателя.
В приведенных уравнениях АД на фазу значения приведены
в системах при расчете на одну установку [6]:

Ток намагничивания по воздушным зазором потока и реактивной индуктивности:
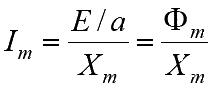
Ток ротора относительно статора и относительно потока воздушного зазора определяется как:
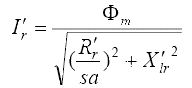
Уравнение для тока намагничивания можно также записать в виде магнитных эффектов насыщения:
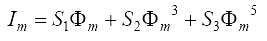
Ток статора по току ротора и тока намагничивания определяется как:
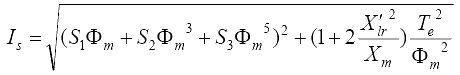
Потери в системе ротора АД разделяются на количество потерь, связанных с конкретными частями машины. Общие потери состоят из потерь в меди статора и ротора, потери в железе, вызванные действием вихревых токов и гистерезиса, паразитных потерь, потери, возникающие в меди и железе двигателя, потери на трение и, наконец, потери сопротивления преобразователя, которое оказывают твердотельные ключи. Потери в меди и железе статора и ротора являются наиболее существенными. Отдельные уравнения потери без учета потери конвертера и кабеля в АД имеют вид [6]:

Приближенные значения потери в преобразователе и инверторе привода АД имеет вид [4]:
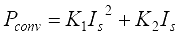
Из данных уравнений, общие потери в системе ротора АД

Общие потери потока относительно воздушного зазора заданы как:

5. ОСП для минимизации потерь двигателя
Многие недавние новшества в области науки, экономики и техники требуют численных методов для поиска глобального оптимума соответствующих задач оптимизации [22]. ОСП базируется на на основе метода стохастического поиска, упоминавшееся впервые Кеннеди и Эберхартом [23]. Механизм ОСП взят из модели комплекса социального поведения, который можем видеть в природе. ОСП может быть представлена концепцией скорости и положения [24]. Два основных уравнения, которые описывают работу ОСП – это вектора скорости (Vid) и радиус-вектор (Xid) задаются как:
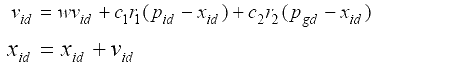
Первая часть уравнения (13) представляет собой инерцию предыдущей скорости, вторая часть является искомой и это говорит нам о личном мышлении частиц, третья часть представляет собой взаимосвязь между частицами и, следовательно, называется социальным компонентом [25]. Постоянные ускорения c1, c2 [26] и значение инерции взаимодействия ω [27] предопределены пользователем, и r1, r2 являются равномерно порожденными случайными числами в диапазоне [0, 1].
Минимизация потерь асинхронного двигателя может быть сформулирована с учетом общих потерь потока относительно воздушного зазора как целевая функция. ОСП ищет оптимальный поток с учетом их максимального предела.
Минимизируется

6. Предомпенсированный системами нечеткой логики ПИ-регулятор
Как правило, сигнал скоростной ошибки, которая представляет собой разницу значения задания скорости и реальной величины, подается на вход в виде скорости. Контроллер обрабатывает ошибки скорости и обеспечивает крутящий момент компонента тока (i*qs) в качестве вывода. Ошибка скорости в любой момент времени определяется как:

где оператор ωr(n)* является заданной скоростью двигателя,
ωr(n) является фактической скоростью двигателя.
ПИ-регулятор скорости является самым простым регулятором, а параметры усиления выбираются путем проб и ошибок при наблюдении их влияния на реакцию привода. Этот контроллер очень чувствителен к вариации параметров, нарушению нагрузки и обладают низкой производительностью при применении непосредственно к системам с существенной нелинейностью [28, 29].
Для того, чтобы преодолеть недостатки ПИ-регулятора, используется НЧПИ-контроллер скорости, описанный в этой статье. Нечеткость предварительной компенсации означает, что сигнал задания скорости ωr(n)* (СЗС) изменяется заранее с помощью нечеткой логики (НЧЛ) в соответствии с частотой вращения ротора ωr(n) (ЧВР), так что получается новый сигнал задания скорости ω*r1 (СЗС). Некоторые особенности, такие как переброс и недолет, происходящие в скорости реакции, которыми обладает контролер, могут быть устранены [30], этот контроллер применим для шахтных подъемных установок, где соотношение крутящего момента и скорости меняется время от времени.
Как обычно, заданием в НЧЛ являются скорость ошибки (ω*re) и изменение скорости ошибки (ωe(n)), и значение на выходе контроллера НЧЛ добавляется к исходной скорости для создания предварительной компенсацией задания скорости (δ), который будет использоваться в качестве сигнала задания скорости с помощью ПИ-регулятора, как показано на рис. 1. Предварительный компенсатор на основе нечеткой логики может быть математически смоделирован следующим образом [28]:

где F является отображением нечеткой логики. Нечеткие множества и правила логики, вычисленные для регулирования частоты вращения, показаны на рис. 4 и в таблице 1 соответственно [28], [30]. ОБ означает отрицательные большие, ОС – отрицательные средние, ОМ – отрицательно малые, НЛ – нулевые, ПБ – положительные большие, ПС – положительные средние и ПМ – положительные малые.
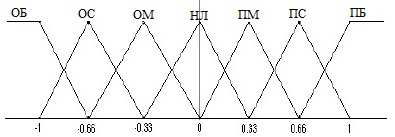
Рисунок 4 – Установки значений для нечеткой логики
Таблица 1 – Логические правила для НЧПИ-контроллера
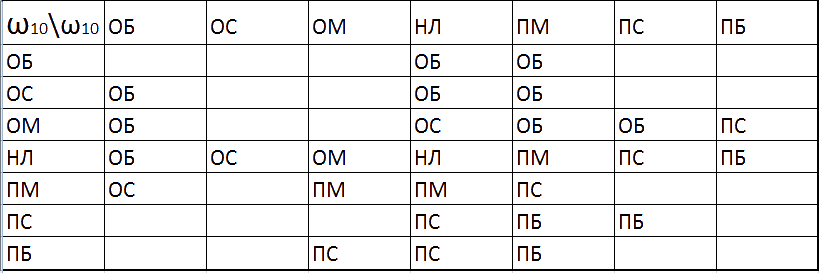
7. Моделирование, резульаты и выводы
В этом разделе рассматривается работа двигателя мощностью 1 л.с. при переменной нагрузке и скорости (для шахтных подъемных установок) для анализа с точки зрения оптимальной энергии и скорости, как показано на рис. 1. Ссылаясь на асинхронный двигатель (1 л.с.), параметры которого приведены в [6], и потери в инверторе [4], минимизация входной мощности осуществляется с помощью трех типов контроллеров, а именно: контроллер постоянного потока, модели потери, основанной на контроллер и контроллере ОСП поиска. В целях повышения стабильности вращения ротора, используется НЧПИ контроллер, и его производительность сравнивается с обычным ПИ-регулятором.

Рисунок 5 – Результаты для постоянного потока операций для ПИ-регулятора: поток, скорость, момент на валу двигателя, мощность постоянного тока
Значения потока, скорости и крутящего момента показаны на рис. 5 (а). Мотор в цепи постоянного тока имеет мощность около 1170 Вт в операционной области t3, как показано на рис. 5 (г).
Контроль постоянного потока
Это обычное управление, ориентированное на поле. Токи или потоки, производящие токи, всегда постоянны, независимо от скорости и крутящего момента, показанные на рис. 5 (а). Мотор предлагается в цепи постоянного тока мощностью почти 1170 Вт в операционной области t3 показано на рис. 5 (г).
Контроль поиска
Для оптимального управления энергией, мощность на входе постоянного тока сосредоточена в данной работе и сводится к минимуму с помощью поисковых управлений, регулируя (уменьшая) токи шаг за шагом до малых значений. Показана зависимость постоянного тока для каждого значения регулировки, как показано на рис. 6 (а). Когда мощность постоянного тока минимизирована, корректировка будет прекращена с сохранением текущего значения потока. Чтобы настроить градиент идентификатора, использовали известный метод [31]. Используя этот контроллер, двигатель подключают в цепь постоянного тока мощностью около 1070 Вт (рис. 6 (г)), которая снижается при 100 Вт по сравнению с постоянным значением работы потока. Кроме управления энергией, этот контроллер создает меньшие колебания скорости и крутящего момента при изменениях в их цепях, как показано на рис. 6 (б, в).
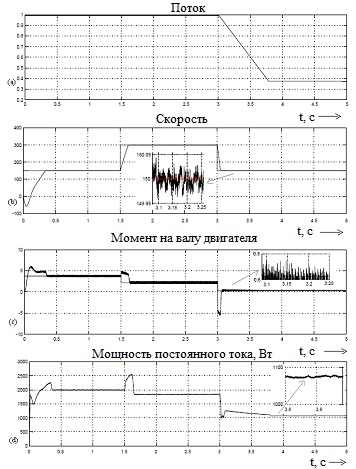
Рисунок 6 – Результаты для контроллера поиска с ПИ-регулятором: поток, скорость, момент на валу двигателя, мощность постоянного тока
Модель потерь, основанная на ОСП-контроллере
ОСП используется для поиска оптимальных токов от модельных потерь АД в соответствии с нагрузкой двигателя и скоростью. Этот контроллер находит оптимальные идентификаторы мгновенно, как показано на рис. 7 (а), вместо плавной регулировки в поисках оптимального управления. Здесь мотор подключают в постоянную цепь 1075 Вт, которая несколько выше, чем при контроле поиска. Это происходит из-за ошибки моделирования двигателя. В случае бросков скорости и крутящего момента, ОСП контроллер показывает гораздо лучшие результаты, чем контроль поиска, как показано на рис. 7 (б) и (в).
На рисунке 8 и 9, НЧПИ контроллер предлагает меньшие колебания скорости (на 60%), чем ПИ-регулятор, не нарушая работу оптимальных контроллеров энергии, но в случае превышения крутящего момента выдают одинаковые результаты. Таким образом, сочетание ОСП и НЧПИ превосходит обычные контроллеры, такие как контроллер поиска для управления энергией и ПИ-контроллер для управления скоростью.

Рисунок 7 – Результаты системы на базе модели потерь с ПИ-регулятором: поток, скорость, момент на валу двигателя, мощность постоянного тока

Рисунок 8 – Результаты моделирования для модели потерь с НЧПИ-контроллером: поток, скорость, момент на валу двигателя, мощность постоянного тока

Рисунок 9 – Результаты для контроллера поиска с НЧПИ-регулятором: поток, скорость, момент на валу двигателя, мощность постоянного тока
7 Оценка ОСП со стандартными эталонными задачами
Для проверки выполнения ОСП используются стандартные задачи теста (показано в Таблице 2). Численные результаты приведены в таблице 3 и графы конвергенции на рис. 10–12. ОСП дала лучшие результаты во всех тестовых задачах.
Это обычные поля ориентированного управления потоком или потоком, создающим ток, значения которых всегда постоянны, независимо от скорости.
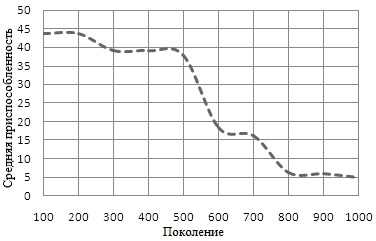
Рисунок 10 – Сходимсть для графика f1
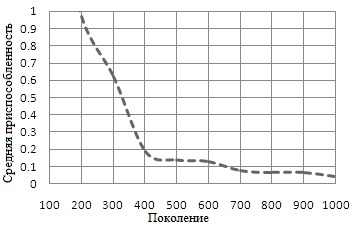
Рисунок 11 – Сходимсть для графика f2

Рисунок 12 – Сходимсть для графика f7
Таблица 2 – Стандартные задачи для проверки ОСП
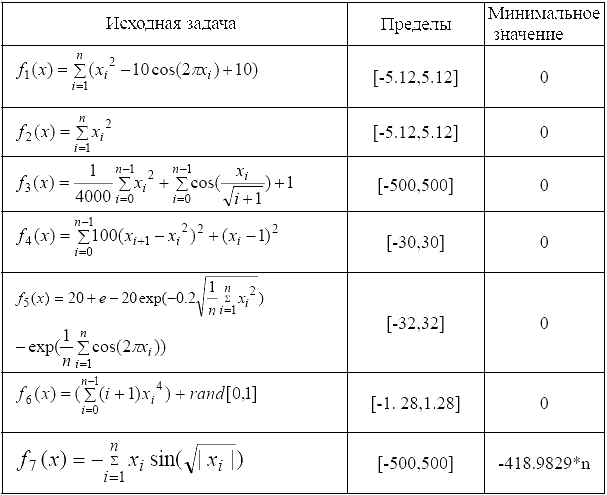
Таблица
3 – Результаты ОСП в исходных
задачах (Средняя приспособленность/стандартное отклонение)

Заключение
В работе исследована важность контроллеров энергосбережения и возможность частичного загруженного трехфазного асинхронного двигателя в шахтных подъемных установках. Вектор контролируемой мощности двигателя мощностью 1 л.с. исследовали в трех измерениях, а именно: постоянный поток операций, поток частиц контроллера с помощью оптимизации потока и поиска контроллера стационарных условиях. Чтобы повысить устойчивость привода при переменной скорости и нагрузке, была принята система нечеткой предварительной компенсации пропорционально-интегрального (НЧПИ) контроллера, и ее результаты сравнили с обычными пропорционально-интегральными (ПИ) контроллерами. По результатам испытаний комбинация ОСП и нечеткой логики превзошли обычные контроллеры и позволили сохранить100 Вт мощности на испытаниях двигателя. Поскольку мощность на шахтных подъемных двигателя высока, значительное количество сбережений (в кВт) возможно. Четыре задачи-теста были использованы для проверки паролей алгоритма.
Подтверждение
Первый автор хотел бы поблагодарить Министерство человеческих ресурсов и развития (МЧРиР), правительство Индии за предоставление финансовой поддержки для его исследовательской работы.
Список использованной литературы
- Z.
Maljkovic, M. Cettolo,
et. al, “The impact of the induction
motor onshort–circuit
current”, IEEE Ind. Application
Magazine, 2001, pp. 11–17.
- M.K. Yoon, C.S. Jeon, S.K. Kauh, “Efficiency increase of aninduction motor by improving cooling performance”, IEEE Trans. Energy Conversion, 2002, pp. 1–6.
- C. Palanichamy, C. Nadarajan, P. Naveen, N.S. Babu, Dhanalakshmi, “Budget constrained energy conservation – An experience with a textile industry”, IEEE Trans. Energy Conversion, Vol. 16, No. 4, 2001, pp. 340–345.
- R. H.A. Hamid, A.M.A. Amin, R.S. Ahmed, A. El-Gammal, “New technique for maximum efficiency of induction motors based on PSO”, IEEE conference proceedings, 2006, pp. 2176–2181.
- D. H. Kim, “GA-PSO based vector control of indirect three phase induction motor”, Applied Soft Computing, Vol. 7, No. 2, 2006, pp. 601–611.
- I. Kioskesidis, N. Margaris, “Loss minimization in scalar controlled induction motor drives with search controller”, IEEE Trans. Power Electronics, Vol. 11, No. 2, 1996, pp. 213–220.
- M. Cacciato, A. Consoli, G. Scarcella, G. Seelba, A. Testa, “Efficiency optimization technique via constant optimal slip control of induction motor drives,” IEEE conference proceedings on Power Electronics, Electric Drives, automation, and Motion, 2006, pp. 32–42.
- B. Pryymak, et al., “Neural network based flux optimization using a model of losses in induction motor drives,” Mathematics and computers in simulation, Vol. 71, 2006, pp. 290–298.
- S. Lim, K. Nam., “Loss minimization control scheme for induction motors,” IEE proc. Electr. Power Appli., Vol. 151, No. 4, 2004, pp. 385–397.
- C. Thanga Raj, S.P. Srivastava, and Pramod Agarwal, “Differential Evolution based Optimal control of Induction Motor Serving to Textile Industry”, Int. J. of Computer Science, Vol. 35, No. 2, 2008.
- S. Ghozzi, K. Jelassi, X. Roboam, “Energy optimization of induction motor drives,” IEEE conference on Industrial Technology (ICIT), 2004, pp. 602–610.
- K. Sundareswaran, et al, “Artificial neural network based voltage controller for energy efficient induction motor drives,” IEEE Int. conference, Dec. 1998, pp. 552–554.
- R.C. Eberhart, Y. Shi, “Comparing inertia weights and constriction factors in particle swarm optimization”, IEEE conference proceedings, 2000, pp. 84–88.
- M. Chilikin, “Electric Drives”, MIR Publishers, Moscow, 1976.
- C. Thanga Raj, Pramod Agarwal, and S.P. Srivatava, “Particle Swarm optimized Induction Motor for a Textile Mill Load Diagram”, Proc. Of IET Int. Conf. ICTES’07, India, Dec. 2007, pp. 379–383.
- P. Gnacinski, “Energy saving work of frequency controlled induction cage machine,” Energy Conversion and Management, Vol. 48, 2007, pp. 919–926.
- M.B. Metwally, F.E. Abdul-Kader, H.M. El-Shewy, M.M. El-Kholy, “Proposed torque optimized behavior for digital speed control of induction motor”, Energy Conversion and Management, Vl. 43, 2006, pp. 1675–1685.
- T.W. Jian, N.L. Schmitz, and D.W. Novotny, “Characteristic induction motor slip values for variable voltage part load performance optimization,” IEEE Trans. Ind. Appl., vol. PAS-102, no. 1, 1984, pp. 38–46.
- M.H. Park, S.K. Sul, “Microprocessor based optimal efficiency drive of an induction motor, “IEEE Trans. Ind. Elec. vol. IE–31, no. 1, 1984, pp. 69–73.
- F. Abrahamsen, “Energy Optimal Control of Induction Motor Drives”, Ph.D Thesis, Aalborg University, 2000.
- R. Krishnan., “Electric motor drives. Modeling, Analysis, and Control,” Prentice Hall of India publication, 2003.
- Fang Wang, Yuhui Qiu, “A modified particle swarm optimizer with Roulette selection operator,” IEEE conference proceedings of NLP-KE, 2005, pp. 765–768.
- J Kennady, R Eberhart. , “Particle swarm optimization”, IEEE international conference on neural networks, NJ, 1995, PP. IV: 1942–1948.
- A.M.A. Amin, M.I. Korfally, A.A. Sayed, O.T.M. Hegazy, “Loss minimization of two asymmetrical windings induction motor based on swarm intelligence,” IEEE conference proceedings, 2006, pp. 1156–1161.
- J. Kennedy, “The Particle Swarm: Social Adaptation of Knowledge”, IEEE International Conference on Evolutionary Computation (Indianapolis, Indiana), IEEE Service Center, Piscataway, NJ, 1997, pp. 303–308.
- R. C. Eberhart and Y. Shi, “Particle Swarm Optimization: developments, Applications and Resources”, IEEE Int. Conference on Evolutionary Computation, 2001, pp. 81–86.
- Y.H. Shi and R.C. Eberhart, “A Modified Particle Swarm Optimizer”, IEEE International Conference on Evolutionary Computation, Anchorage, Alaska, 1998, pp. 69–73.
- Jong-Hwan Kim, Kwang-Choon Kim, and Edwin K.P. Chong, “Fuzzy Pre-Compensated PID Controllers’, IEEE Trans. Control System, Vol. 2, No. 4, 1994, pp. 406, 411.
- Seon-Woo Lee, Moon-Jong Jeong, Bo-In Jang, Chang-Hyun Yoo, Sang-Gweon Kim, and Yoon-Ser Park, “Fuzzy Pre-Compensated PI Controller for A Variable Capacity Heat Pump”, Proc. IEEE Conf. Control Applications, Italy, 1998, pp. 953–957.
- Bhim Singh and Ghatak Choudhuri, “Fuzzy Logic Based Speed Controllers for Vector Controlled Induction Motor Drive,” in proc. November-December 2002, IETE Journal of Research, vol.48, no.6, pp. 441–447.
- Chandan Chakraborty, Minh C. Ta, Toshiyuki Uchida and Yoichi Hori, “Fast Search Controllers for Efficiency Maximization of Induction Motor Drives Based on DC Link Power Measurement”, Proc. of IEEE Conf. PCC-Osaka, 2002, pp. 402–408.