Fractal music is one slice of the study of fractals in general. 'Fractal' is the name given to images, landscapes, sounds, and any other pattern that is self-similar in nature, that is, if you look at one small part, no matter how small, you get a sense of the whole picture.

The possibility of using fractal methods to create music was first mentioned upon the discovery that all music, regardless of culture, followed the patterns of fractal motion or 'pink noise.' Pink noise is somewhere in between white noise (complete chaos, far too disorderly to be considered musical) and brown noise (very orderly, and too dull to sound like music). Thus, the question arose: if fractal methods produce pink noise, and all music resembles pink noise, is it possible to produce music using fractal methods?

This question is the focus of our research.

We want to use two basic methods to create our fractal music.

The first method is called L-Systems. To briefly describe L-Systems, they create the self-similarity of fractals, starting with a short string of symbols and replacing the symbols with corresponding rules (which are their own strings of symbols that can be replaced). The symbols are then interpreted as notes, chords, and several other things.

The second method involves Fractal Motion. Fractal motion (pink noise) is generated with various random number methods, starting with a straight line and repeatedly altering portions of the line.

These are only brief descriptions of our methods. The daring can learn more by reading further.

The fractal music methods we have used produce a wide variety of songs. Many of our pieces follow the conventions of Western music, but that is only due to constraints we placed on them to add an air of familiarity to our tunes. In several of our pieces, the keen ear can detect some repeated themes and self-similarity inherent in the music.

We did experiment as to what methods and what parameters sounded the best, especially with the fractal motion method. Our findings were that music with a fractal dimension near 1.4 sounded the best (the fractal dimension is a measure of how close to white or brown noise the fractal is). The authors' personal favorite tunes are those generated by the single note L-Systems and the chord progression L-Systems. [1]

An L-system or Lindenmayer system is a parallel rewriting system, namely a variant of a formal grammar, most famously used to model the growth processes of plant development, but also able to model the morphology of a variety of organisms.[2] A L-system consists of an alphabet of symbols that can be used to make strings, a collection of production ruleswhich expand each symbol into some larger string of symbols, an initial "axiom" string from which to begin construction, and a mechanism for translating the generated strings into geometric structures. L-systems can also be used to generate self-similar fractals such as iterated function systems. L-systems were introduced and developed in 1968 by the Hungarian theoretical biologist and botanist from the University of Utrecht, Aristid Lindenmayer (1925–1989).

L-systems structure. The recursive nature of the L-system rules leads to self-similarity and thereby fractal-like forms are easy to describe with an L-system. Plant models and natural-looking organic forms are easy to define, as by increasing the recursion level the form slowly 'grows' and becomes more complex. Lindenmayer systems are also popular in the generation of artificial life.

L-system grammars are very similar to the semi-Thue grammar (see Chomsky hierarchy). L-systems are now commonly known as parametric L systems, defined as a tuple G = (V, ω, P), where V (the alphabet) is a set of symbols containing elements that can be replaced (variables); ω (start, axiom or initiator) is a string of symbols from V defining the initial state of the system; P is a set of production rules or productions defining the way variables can be replaced with combinations of constants and other variables. A production consists of two strings, thepredecessor and the successor. For any symbol A in V which does not appear on the left hand side of a production in P, the identity production A → A is assumed; these symbols are called constants or terminals.

The rules of the L-system grammar are applied iteratively starting from the initial state. As many rules as possible are applied simultaneously, per iteration; this is the distinguishing feature between an L-system and the formal language generated by a formal grammar. If the production rules were to be applied only one at a time, one would quite simply generate a language, rather than an L-system. Thus, L-systems are strict subsets of languages.

An L-system is context-free if each production rule refers only to an individual symbol and not to its neighbours. Context-free L-systems are thus specified by either a prefix grammar, or aregular grammar. If a rule depends not only on a single symbol but also on its neighbours, it is termed a context-sensitive L-system.

If there is exactly one production for each symbol, then the L-system is said to be deterministic (a deterministic context-free L-system is popularly called a D0L-system). If there are several, and each is chosen with a certain probability during each iteration, then it is a stochastic L-system.

Using L-systems for generating graphical images requires that the symbols in the model refer to elements of a drawing on the computer screen. For example, the program Fractint usesturtle graphics (similar to those in the Logo programming language) to produce screen images. It interprets each constant in an L-system model as a turtle command. [3]

Strings of Notes. The most straightforward interpretation is to assign each symbol directly to its corresponding note on the musical staff -- "A" to A, "B" to B, etc., as well as throwing some extra symbols in such as "R" for a rest. Our above string of letters would become this:

Variations on this method include assigning each of the letters to a percussion instrument. To pick our axioms and production rules, we resorted to spelling out words and pulling short excerpts from human-composed pieces.

Another interpretation of the L-System strings is as a chord progression... consider this following system.

Axiom: I. Production Rules: I - I IV V I; ii - ii V I IV; IV - IV V I ii; V - V I ii V.

After two iterations, this produces a chord progression:I IV V I IV V I ii V I ii V I IV V I.

This method is not very effective when used alone, but is excellent when used in conjunction with other methods, either as background chords or to further constrain melodies to give them more of a traditional Western music feel.

Turtle graphics is a term in computer graphics for a method of programming vector graphics using a relative cursor (the "turtle") upon a Cartesian plane. Turtle graphics is a key feature of the Logo programming language. The turtle has three attributes: a position, an orientation, a pen, itself having attributes such as color, width, and up versus down. The turtle moves with commands that are relative to its own position, such as "move forward 10 spaces" and "turn left 90 degrees". The pen carried by the turtle can also be controlled, by enabling it, setting its color, or setting its width. A student could understand (and predict and reason about) the turtle's motion by imagining what they would do if they were the turtle. Seymour Papert called this "body syntonic" reasoning.

From these building blocks one can build more complex shapes like squares, triangles, circles and other composite figures. Combined with control flow, procedures, and recursion, the idea of turtle graphics is also useful in a Lindenmayer system for generating fractals.

Turtle geometry is also sometimes used in graphics environments as an alternative to a strictly coordinate-addressed graphics system. [4]

In the Turtle Graphics interpretation, there are four basic symbols, "F", "f", "+", and "-". Instead of being assigned directly to notes or chords, they are interpreted as instructions to "draw" a melody. In the traditional visual interpretation, these control a virtual "turtle" holding a pencil. The commands mean "Move forward one unit, and draw a line", "Move forward one unit, but don"t draw a line", "turn d degrees to your left", and "turn d degrees to your right", respectively. The result is a picture like the one at right.

The Sierpinski triangle drawn using an L-system. Variables : A B; constants : + − ; start : A ; rules : (A → B−A−B), (B → A+B+A) ; angle : 60°.

Here, A and B both mean "draw forward", + means "turn left by angle", and − means "turn right by angle" (see turtle graphics). The angle changes sign at each iteration so that the base of the triangular shapes are always in the bottom (they would be in the top and bottom, alternatively, otherwise).

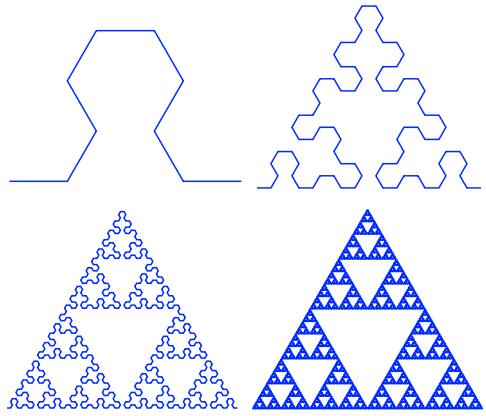
Evolution for n = 2, n = 4, n = 6, n = 8

There is another way to draw the Sierpinski triangle using an L-system. Variables : F G; constants : + −; start : F−G−G; rules : (F → F−G+F+G−F), (G → GG); angle : 120°; Here, F and G both mean "draw forward", + means "turn left by angle", and − means "turn right by angle".

In our musical interpretation, horizontal motion was seen as note length, while vertical motion was seen as change in pitch. The above drawing would be interpreted like this:

This method also had its variations, such as a "trill next note" command as well as a system of marking pitches and returning to that pitch at a later time.

One of the great advantages in involving an obviously creative area such as music in mathematics teaching is that it leads immediately to many extensions. Students are naturally keen to come up with improvements on the basic algorithm which make the resulting music more pleasant to the ear. These improvements could be mathematically motivated, such as trying to change the autocorrelation structure. They could also be reproduced such as changing the scale used to produce modal music or introducing a second instrument.

1. MusiNum. http://www.tursiops.cc/fm/
2. The mathematical theory of L systems (Academic Press, New York, 1980).
3. L-systems. http://en.wikipedia.org/wiki/L-system#cite_note-0
4. Turtle fractal. http://en.wikipedia.org/wiki/Turtle_graphics