DonNTU   Masters' portal

Abstract

Content

Introduction

The problem of image analysis, video and other data is very urgent today, especially in medicine. Volume segmentation is an important component of medical applications for diagnosis and analysis of anatomical data. Along with the rapid development of computer technology sharply raises the question of developing methods and approaches to medical image processing. Often, the correct diagnosis of the disease is based on information obtained through magnetic resonance imaging, positron-emission research, X-ray and others. In this connection there is need to develop efficient algorithms for segmentation and volume segmentation in particular. Manual processing of three-dimensional images requires a great deal of efforts and is often fraught with errors. Interpretation of the same three-dimensional medical image reconstruction requires medical way of thinking and can lead to misunderstandings. The algorithms that automate this process may help doctors cope with large amounts of data, providing them with reliable support for the diagnosis and treatment.

1. Theme urgency

With the growth of technical capabilities of modern computer systems, there appear more and more possibilities for data processing. Technological progress has touched the medicine as well. In clinics and hospitals a large number of complex devices and software and hardware are used. However, despite all the variety of technical tools available to physicians, they still have a great number of problems. One of them is the medical image processing. The complexity of the analysis and data amounts are very large. These entails a complex process and a high probability of errors without any means of automatization. In this connection, the problem of automatization the process of medical image analysis and segmentation in particular, is important.

2. Goals and tasks of research

The goal of the research is to improve the segmentation of three-dimensional medical images obtained by computing tomography.

The main tasks of research:

  • to develop an evolutionary algorithm for segmentation of medical images;
  • perform a parallel implementation of the algorithm;
  • offer tools of three-dimensional medical image segmentation.

    • 3. Scientific novelty and scope

    Segmentation of three-dimensional medical images provides a wide range of possibilities for the study of anatomical structures without direct contact with the patient. For example, data obtained by MRI or CT scan, enable you to create a virtual map of blood vessels, gastrointestinal tract, to explore areas of interest (tissues, organs, tumors and other sites). Today, there is a wide variety of algorithms for segmentation of three-dimensional images, which gives the best results. However, there is no universal algorithm that is appropriate for any class of data. In addition, various algorithms behave differently when processing large amounts of data. In this regard, it is advisable to develop an algorithm that would simultaneously solve computationally difficult problems in a reasonable time, and would be resistant to noise and artifacts.

    4. The general formulation of the problem

    A geometric description of the three-dimensional body, resulting from measurement of the actual physical object, using three-dimensional scanner, or CT is called volume image. By segmentation we mean a partition of the image on some areas which are not alike according to the brightness characteristics, texture, etc. The segmentation is generally considered to be a very difficult task. This difficulty arises because of the large amounts of data, the complexity and variability of the studied areas. The situation is aggravated by the image defects such as the presence of artifacts and noise, which can lead to the fact that the boundaries of anatomic structures have become blurred. Thus, the main task of segmentation algorithms is to extract the exact boundaries of organs or areas of interests and their separation from the rest of the data. Nowadays there are many approaches to image segmentation. They vary depending on the application area, the image modality (CT, MRI, etc.) and other factors. For example, the segmentation of the lungs has features that are not typical of the small intestine. Algorithm that gives good results for one area may not work for another. This variability makes the segmentation very difficult. At present there is no method of segmentation, which provides acceptable results for all types of medical data. There are generic techniques that can be applied to a large number of diverse data. But the methods that are designed for particular cases, always give the best results. The authors of [1] classify the variety of segmentation algorithms as follows.

    1. Structural algorithms;
    2. Stochastic algorithms;
    3. Combined algorithms.

    These algorithms are algorithms for finding optimal solutions. It should be noted that although these methods solve the task to some extend, they are not without drawbacks. The main disadvantages are:

  • high computational complexity when a large amount of data is being processed;
  • loss of use of memory resources;
  • the sensitivity of some algorithms to noise;
  • the need to specify additional information;
  • the need to set some parameters;
  • poor results with images, in which the brightness characteristics of the area differ slightly.

    • 4.1 Segmentation using clustering methods

    One option to overcome most of the problems outlined is the use of algorithms that provide suboptimal solutions – namely, the evolutionary algorithms. Note that in the formulation of the problem of segmentation, there is the analogy with the problem of clustering. In order to reduce the problem of segmentation to the problem of clustering, it is necessary to specify the mapping of pixels in a feature space and introduce a metric (a measure of proximity) in this feature space. As the signs point in the image, you can use the representation of colors in a color space. An example of a metric can be Euclidean distance between vectors in the feature space. Then the result of clustering will be the color quantization of an image. Specifying the mapping in the feature space, you can use any method of cluster analysis. The most popular clustering methods used for image segmentation are the method of K-means, FCM, and other algorithms [2]. The main drawback of cluster analysis techniques is that they are sensitive to noise.

    Another approach to solving the problem of segmentation is to combine the genetic algorithm and K-means algorithm. Let's consider an evolutionary version of the K -means algorithm. Suppose we have a set A = {x1, x2, ..., xn} – of vectors of length d, where the element xij – is the i-th property of the j-th element of A. We introduce the following matrix . The matrix W has the following important property:

    , (1)

    Let’s denote the centers of the clusters as follows , then

    (2)

    Thus the deviation of the cluster can be determined by the formula:

    (3)

    It is required to find a matrix that . Since the search space is the set of all existing binary matrices W, satisfying (2), the chromosome can be represented as a string of length n, and each allele can take values from the set {1, 2,..., K}. Initialization of the population can be carried out by one of the classical methods.

    Selection involves the choice of a random chromosome from the population using the roulette or any other method. The solution to the current population may define some weight, which affects the survival of the next generation. This means that each individual is given a number, or the calculated value of the special fitness function. There are many ways of calculating this fitness function [3]. The authors of [2] propose the following variant of the solution. Let , where – the mean and standard deviation of respectively, – a constant. Then the value of fitness function is defined as follows:

    (4)

    The mutation operator changes the value of the allele, depending on the distance from this point to the center of the cluster. We define it as follows: allele is replaced by values, that are selected at random, according to the following probability distribution:

    ,(5)

    where – is a constant, .

    The algorithm presented above by the operator selection may converge for a long time. In addition, the probability of mutation must be quite small, since larger values lead to oscillations of solutions. To avoid such situations we introduce a new operator, called the K-means operator (KMO) [2]. Execution of this operator consists of the following two steps.

    1. We calculate the cluster centers according to the formula (3);
    2. Each data point is reassigned to the nearest cluster center, thus forming a new matrix W.

    With the technique of constructing the initial population and genetic operators, we can construct a genetic algorithm, a block diagram is shown in Fig 1.

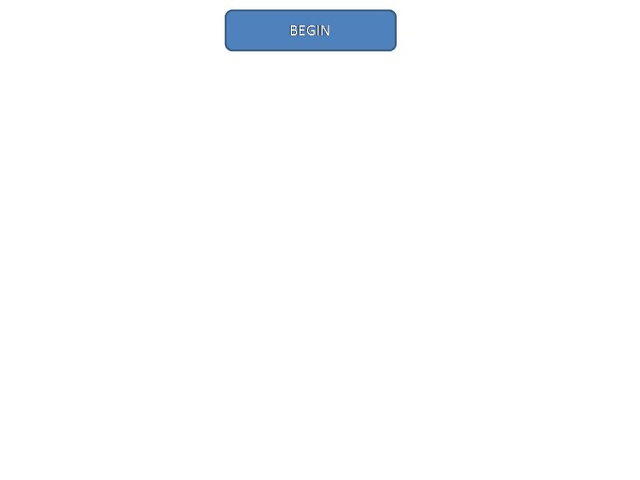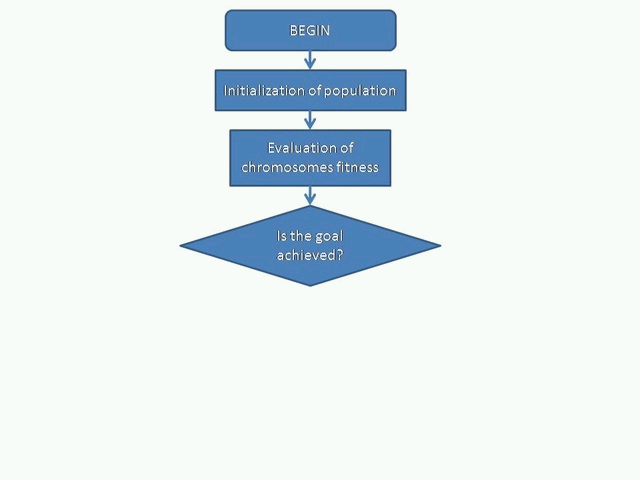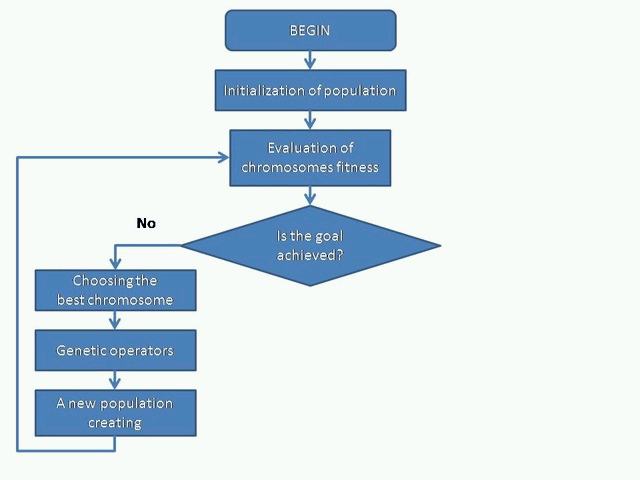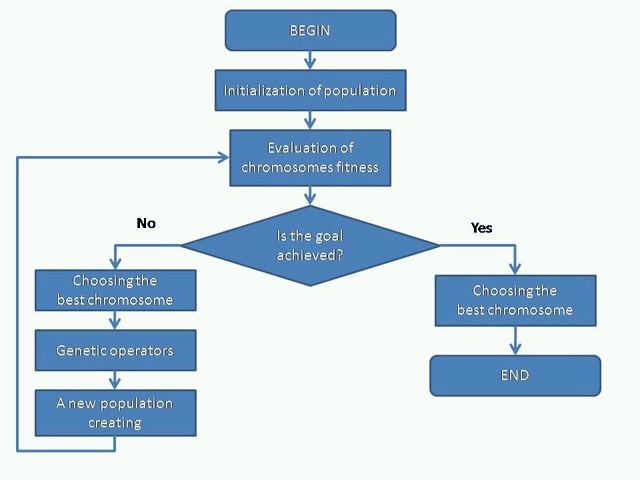
    Fig 1. The general scheme of the genetic algorithm

    4.2 Segmentation using swarm algorithms

    The problem of image segmentation can be reduced to an optimization problem on graphs [1]. This allows to use ant colony algorithm to solve it. The idea of ant algorithm is as follows. There is a simulation of the behavior of ants associated with their ability to find quickly the shortest path from nest to a food source and adapt to changing conditions, finding a new shortest way. In its motion the ant leaves a pheromone along the way, and this information is used by other ants to choose the path. This is an elementary rule of conduct and it determines the ability of ants to find a new path, if the old one is not available. There is also modeling of the way of enrichment and the pheromone evaporation. These steps of the algorithm help find all possible optimal paths in the search space, and not only one particular way. Regardless of the modification the general idea of the ant algorithm can be demonstrated by the block diagram shown in Fig 2.

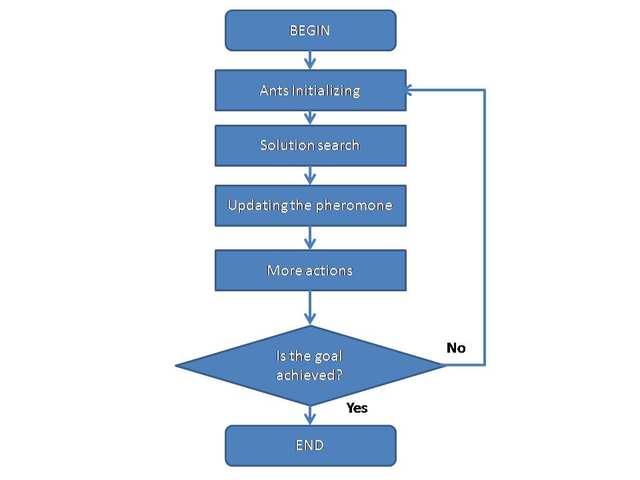
    Fig 2. The general scheme of the ant algorithm

    Initialization of ants is a starting point, where the ant is placed, depends on the constraints imposed by conditions of the problem, because for each task, the way ants’ placement is crucial. Either they all are placed in one spot, or with different repetitions or without repetitions. At this stage, the initial level of pheromone is given. It is initialized to a small positive number so that the initial step, the probability of transition to the next peak is not zero. The transition probability from vertex to vertex is defined by the following formula:

    ,(6)

    where is the set of possible vertices connected with vertex i for ant k, – the level of the pheromone, – heuristic distance, – are constants.

    Pheromone is updated by the following formula:

    ,(7)

    where – the number of ants, – the intensity of evaporation, – the length of road constructed k-th ant at time t, Q – the parameter value.

    Let's consider how to apply ant colony algorithm to image segmentation. In this algorithm, the ants are simple agents that randomly move around the discrete array. Pixels that are scattered in the array elements can be moved from one array to another to form clusters. Moving Pixels are indirectly determined by the behavior of ants. Each ant can add or delete a pixel according to the function that computes the similarity of the pixel to other pixels in the cluster. Thus, the ants are dynamically clusterising images into independent clusters that include only similar to each other pixels. In addition, the agent introduce new probabilistic rules for joining or excluding pixels, as well as the strategy for the local movement for accelerating the convergence of the algorithm. Suppose the dimension of the array is equal to N. Each element of the array is associated with a nest of ants in a manner that allows the ants to move easily from one element to another. In the process of the algorithm ants can modify, or remove the existing building clusters of pixels. A cluster is a combination of two or more pixels, and spatially located in a single cell of the array, making it easy to identify. Let’s initialize N pixels {P1, P2 ..., Pn} to cluster, located in the array so that each array element is associated with only one pixel. Each ant colony with the ai of the ants to
    {a1, a2,..., ak} appends a randomly selected pixel of the array elements and returns to the nest. After the initial phase of the initialization phase is clustering. The choice of an ant is at random. He moves from his nest to the elements of the array and determines with the help of probabilistic rules which pixel to add to the cluster. Each ant knows the location of a list of pixels that are not connected by other ants. An ant determines the next pixel from the free list at random. This algorithm is repeated for each ant. Completion of the algorithm occurs with a specified stopping criterion.

    4.3 Performance

    Attention is drawn to the fact that evolutionary algorithms are quite slow. Therefore, in addition to the basic task of designing an evolutionary segmentation algorithm performance problem must be solved. The latter can be achieved through a combination of CPU and GPU. It is also necessary to pay attention to the fact that evolutionary algorithms are a number of independent or weakly dependent tasks. This gives a high potential for parallelization. Thus, combining the ability of evolutionary algorithms to solve computationally difficult problems and possibilities of modern computer systems, it is theoretically possible to achieve high performance of the slow methods.

    Fig 3. Basic principles of the algorithm design

    Conclusion

    The main pursued goal is to build a well-parallelized version of an evolutionary algorithm that is able to solve the task in a reasonable time, with enough processing large data sets, as well as, if necessary, by combining the CPU and GPU. It is easy to see that the presence of many simple, almost independent of each other agents, provides good potential for parallelization of the algorithm. Based on the said above, it can be concluded that the use of evolutionary and swarms computing may help eliminate some of the shortcomings of known methods for processing three-dimensional images. It is shown that clustering method and a genetic algorithm can be used in one approach. An alternative way is to use the ant colony algorithm for solving the problem of clustering, reduced to an optimization problem on graphs. Analysis of the proposed solutions has shown that genetic algorithms and ant colony algorithm based on a number of independent subproblems, can significantly increase the speed of their work by performing calculations with the use of parallelism in the CPU, as well as the GPGPU. Thus, the direction of future work is the development and implementation of parallel computational schemes for the evolutionary version of the algorithm K-means clustering algorithm and ant images, as well as their validation on the tasks of clustering and classification of CT and MRI images.

    Important Notice

    In writing this essay master's work is not yet complete. Final completion: December 2012. The full text of the work and materials on the topic can be obtained from the author or his head after that date.

    Список источников

    1. Sarang Lakare, Arie E. Kaufman. 3D Segmentation Techniques for Medical Volumes // Center for Visual Computing, Department of Computer Science, State University of New York at Stony Brook. [Электронный ресурс]. – Режим доступа: http://www.cs.sunysb.edu.
    2. Александр Вежневец, Ольга Баринова. Методы сегментации изображений: автоматическая сегментация // Компютерная графика и мультимедаи сетевой журнал. [Электронный ресурс]. – Режим доступа: http://www.cgm.computergraphics.ru.
    3. K. Krishna, M. Narasimha Murty. Genetic K-Means Algorithm // IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B: CYBERNETICS, VOL. 29, NO. 3, JUNE 1999. [Электронный ресурс]. – Режим доступа: http://eprints.iisc.ernet.in.
    4. Р.В. Дрындик, М.В. Привалов. Применение эволюционных вычисления для сегментации трехмерных медицинских изображений/ Сборник материалов к III Всеукраинской научно-технической конференции студентов, аспирантов и молодых ученых. – Донецк, ДонНТУ – 2012, с. 480 – 484.
    5. D. Goldberg. Genetic Algorithms in Search, Optimization and Machine Learning. Reading, MA: Addison-Wesley, 1989.
    6. C. von der Malsburg. The correlation theory of brain function. Technical report, Max-Planck-Institute Biophysical Chemestry, 1981.
    7. G.P. Babu and M.N. Murty. "Simulated annealing for selecting initial seeds in the K-means algorithm" Ind. J. Pure Appl. Math., vol. 25, pp. 85–94, 1994.
    8. J.N. Bhuyan, V.V. Raghavan, and V.K. Elayavalli. "Genetic algorithm for clustering with an ordered representation" in Proc. 4th Int. Conf. Genetic Algorithms. San Mateo, CA: Morgan Kaufman, 1991.
    9. D.R. Jones and M.A. Beltramo "Solving partitioning problems with genetic algorithms" in Proc. 4th Int. Conf. Genetic Algorithms. San Mateo, CA: Morgan Kaufman, 1991.
    10. G.P. Babu and M.N. Murty. "A near-optimal initial seed selection in K-means algorithm using a genetic algorithm" Pattern Recognit. Lett., vol. 14, pp. 763–769, 1993.
    11. G.P. Babu. "Connectionist and evolutionary approaches for pattern clustering" Ph.D. dissertation, Dept. Comput. Sci. Automat., Indian Inst. Sci., Bangalore, Apr. 1994.
    12. G. Rudolph. "Convergence analysis of canonical genetic algorithms" IEEE Trans. Neural Networks, vol. 5, no. 1, pp. 96 – 101, 1994.
    13. L. Davis, Ed., Handbook of Genetic Algorithms. New York: Van Nostrand Reinhold, 1991.
    14. H. Spath, Clustering Analysis Algorithms. New York: Wiley, 1980.
    15. Y.T. Chien. Interactive Pattern Recognition. New York: Marcel-Dekker, 1978.