ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Задача аналізу зображень, відео та інших даних є дуже актуальною в поданий час, особливо в медицині. Просторова сегментація – важлива складова медичних програм з діагностики та аналізу анатомічних даних. Разом зі стрімким розвитком обчислювальної техніки гостро постає питання про розробку методів і підходів до обробки медичних зображень. Найчастіше постановка правильного діагнозу хвороби грунтується на інформації, що була отримана за допомогою магнітно-резонансного дослідження, позитронно-емісcіонного дослідження, рентгена та інших. У зв’язку з цим виникає необхідність в розробці ефективних алгоритмів сегментації і, зокрема, просторової сегментації. Ручна обробка тривимірних зображень вимагає великих зусиль і часто чревата помилками. Інтерпретація ж тривимірного медичного зображення вимагає від лікарів перебудови способу мислення і може призводити до великих різночитань. Алгоритми, що автоматизують цей процес, можуть допомогти медикам впоратися з великим обсягом даних, забезпечивши їм при цьому надійну підтримку для діагностики і лікування.

1. Актуальність теми

У зв’язку із зростанням технічних можливостей сучасних обчислювальних систем з’являється все більше і більше можливостей по обробці даних. Технічний прогрес не обійшов стороною медицину. У клініках і лікарнях використовується велика кількість складних приладів і апаратно-програмних комплексів. Проте не дивлячись на всю різноманітність технічних засобів, доступних медикам, все ще залишається відкритим ряд проблем. Однією з таких проблем є обробка медичних зображень. Складність аналізу та обсяги даних бувають дуже великими. Це призводить до високої складності обробки даних і високій ймовірність помилки при відсутності будь-яких засобів автоматизації. У зв’язку з цим проблема автоматизації процесу аналізу медичних зображень і сегментації, зокрема, є актуальною.

2. Мета і завдання дослідження

Метою дослідження є підвищення ефективності сегментації тривимірних медичних зображень, отриманих за допомогою комп’ютерної томографії.

Основні задачі дослідження:

  • розробити еволюційний алгоритм сегментації медичних зображень;
  • виконати паралельну реалізацію розробленого алгоритму;
  • запропонувати інструментальні засоби сегментації тривимірних медичних зображень.

    • 3. Наукова новизна у області застосування

    Сегментація тривимірних медичних зображень створює широкий спектр можливостей по дослідженню анатомічних структур без безпосереднього контакту з пацієнтом. Так, наприклад, дані, отримані за допомогою МРТ або КТ, дають можливість створювати віртуальні карти кровоносних судин, кишкового тракту, досліджувати області інтересу (тканини, органи, пухлини, інші ділянки). На сьогоднішній день існує велика різноманітність алгоритмів сегментації тривимірних зображень, що дають оптимальні результати. Однак не існує єдиного універсального алгоритму, придатного до будь-якого класу даних. Крім того, різні алгоритми ведуть себе по-різному при обробці досить великих обсягів даних. У зв'язку з цим доцільно розробити алгоритм, який міг би одночасно вирішувати обчислювально важкі задачі за прийнятний час та був би стійкий до шумів і артефактів.

    4. Загальна постановка проблеми

    Просторовим зображенням будемо називати геометричне опис тривимірного тіла, отриманого в результаті виміру реального фізичного об’єкта, наприклад, за допомогою тривимірного сканера або КТ. Під сегментацією будемо розуміти розбиття зображення на несхожі області за деякими ознаками. В якості таких ознак можна брати характеристики яскравості, текстуру тощо. Сегментація, як правило, вважається дуже важкою задачею. Ця важкысть виникає через велику кількість даних, складності і змінність досліджуваних ділянок. Ситуація ускладнюється недоліками зображення, такими, як наявність артефактів і шуму, які можуть привести до того, що межі анатомічних структур стають нечіткими. Таким чином, основне завдання алгоритмів сегментації – пошік точних ділянок органів або областей інтересів і відділення їх від інших даних. На сьогоднішній день існує дуже багато підходів до сегментації зображень. Вони різняться в залежності від галузі застосування, модальності зображення (КТ, МРТ і тощо) та інших факторів. Наприклад, сегментація легенів має особливості, які не характерні для тонкого кишечника. Алгоритм, який дає хороші результати для однієї області, може не працювати для іншої. Ця змінність робить сегментацію дуже складним завданням. В поданий час не існує методу сегментації, який забезпечує прийнятні результати до будь-якого типу медичних даних. Існують узагальнені методи, які можуть бути застосовані до великої кількості різноманітних даних. Але методи, які призначені для окремих випадків, завжди дають найкращі результати. Автори [1] класифікують все різноманіття алгоритмів сегментації наступним чином:

  • структурні алгоритми;
  • стохастичні алгоритми;
  • комбіновані алгоритми.

    • Подані алгоритми відносяться до алгоритмів пошуку оптимальних рішень. Слід зазначити, що хоча дані методи в тій чи іншій мірі вирішують поставлену перед собою задачу, вони не позбавлені недоліків. До основних недоліків можна віднести:

  • високу обчислювальну складність при великому обсязі оброблюваних даних;
  • програш у використанні ресурсів пам’яті;
  • чутливість деяких алгоритмів до шумів;
  • необхідність в завданні додаткової інформації;
  • необхідність в налаштуванні деяких параметрів;
  • погані результати роботи із зображеннями, на яких характеристики яскравості області розрізняються незначно.

    • 4.1 Сегментація за допомогою методів кластеризації

    Один з варіантів подолання частини з викладених проблем – використання алгоритмів, що дають субоптимальних рішення, а саме – еволюційних алгоритмів. Зауважимо, що в постановці задачі сегментації простежується аналогія із задачею кластеризації. Для того, щоб звести задачу сегментації до задачі кластеризації, необхідно задати відображення точок зображення в деякий простір ознак і ввести метрику (міру близькості) на цьому просторі ознак. В якості ознак точки зображення можна використовувати дані ії кольору в деякому колірному просторі. Прикладом метрики може бути евклідова відстань між векторами в просторі ознак. Тоді результатом кластеризації буде квантування кольору для зображення. Задавши відображення в простір ознак, можна скористатися будь-якими методами кластерного аналізу. Найбільш популярні методи кластеризації, що використовуються для сегментації зображень, – метод K-середніх, FCM та інші алгоритми [2]. Основним недоліком методів кластерного аналізу є те, що вони чутливі до шумів.

    Інший підхід до вирішення задачі сегментації полягає в комбінуванні генетичного алгоритму та алгоритму К-середніх. Розглянемо еволюційний варіант алгоритму K-середніх. Нехай дана множина A = {x1, x2,..., xn} – множина векторів довжини d, при цьому елемент xij – це i-а властивість j-го елементу множини А. Введемо наступну матричну величину . Матриця W має наступну важливу властивість:

    , (1)

    Позначимо центри кластерів наступним чином , тогда

    (2)

    Таким чином, кластерне відхилення може бути визначено за формулою:

    (3)

    Потрібно знайти таку матрицю , що . Простір пошуку є множиною всіх існуючих двійкових матриць W, що задовольняють умові (2), отже можна представити хромосому у вигляді рядка довжини n, при цьому кожен аллель може приймати значення з множини
    {1, 2, ..., K}. Ініціалізація популяції може бути здійснена одним з класичних методів.

    Селекція передбачає вибір випадкової хромосоми з популяції за допомогою методу рулетки, або будь-якого іншого методу. Рішення в поточній популяції може задавати певну вагу, що впливає на виживання хромосом в наступному поколінні. Це означає, що кожній особі задається деяке число, або обчислюється значення спеціальної фітнес-функції. Існує багато засобів обчислення цієї фітнес-функці [3]. Автори [2] пропонують наступний варіант рішення. Нехай , де – середнє значення і стандартне відхилення функції відповідно, – деяка константа. Тоді значення фітнес-функції визначимо наступним чином:

    (4)

    Оператор мутації змінює значення алелю в залежності від відстані від поданої точки до центру кластера. Задамо його наступним чином: аллель замінюється значеннями, які вибираються випадково, згідно з наступним розподілом ймовірностей:

    ,(5)

    де – деяка константа, .

    Алгоритм, з представленим вище оператором селекції, може сходитися досить довго. Крім того, ймовірність мутації повинна бути досить мала, тому що великі значення ведуть до коливань рішень. Щоб вилучити такі ситуації, вводиться новий оператор, що називаєтся K-means operator (KMO) [2]. Виконання поданого оператора складається з наступних двох кроків:

    1. обчислюються центри кластерів за формулою (3);
    2. кожна точка даних перепризначається кластеру з найближчим центром, тим самим формується нову матрицю W.

    Маючи техніку побудови початкової популяції і генетичні оператори, можна побудувати генетичний алгоритм, блок-схема якого представлена на мал 1.

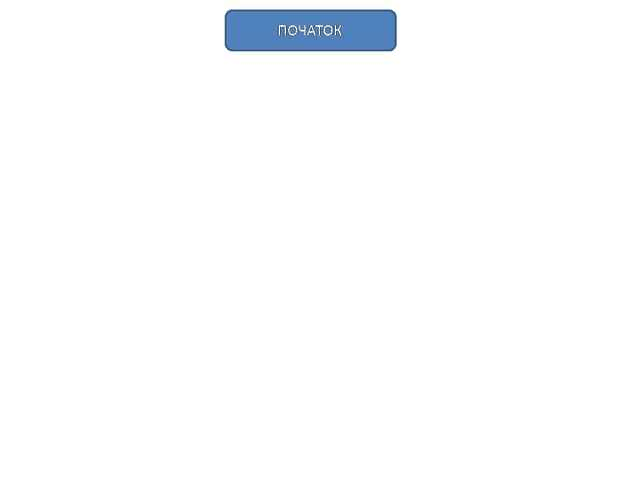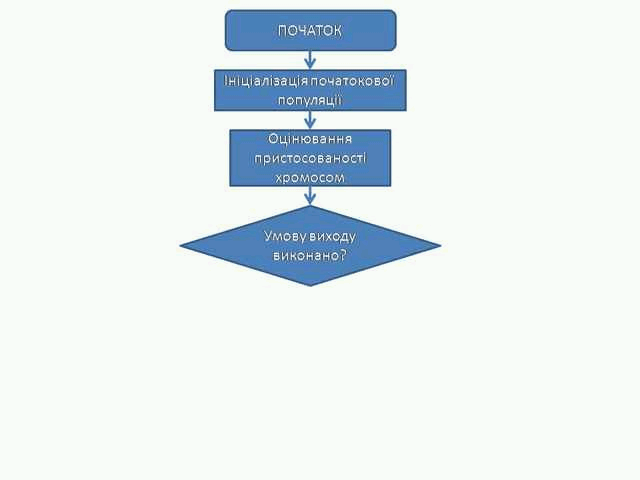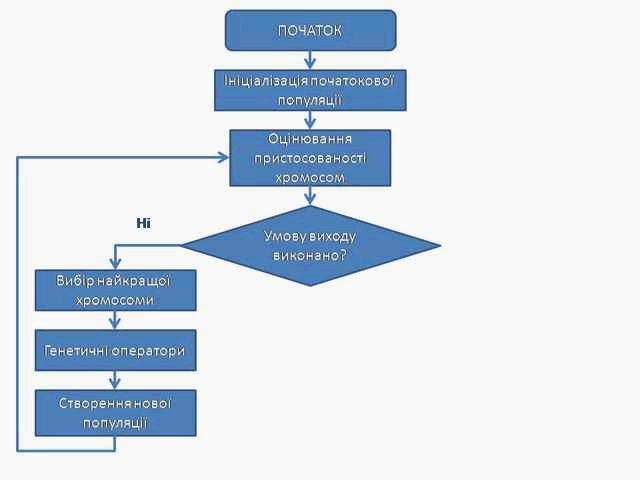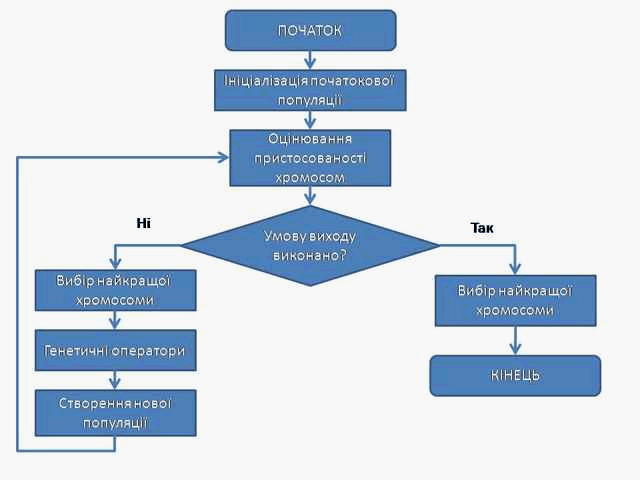
    Мал 1. Загальна схема роботи генетичного алгоритму

    4.2 Сегментація за допомогою ройових алгоритмів

    Задача сегментації зображень також може бути зведена до задачі оптимізації на графах [1]. Така специфіка завдання дозволяє використовувати алгоритм мурашиних колоній для її вирішення. Ідея мурашиного алгоритму полягає в наступному. Відбувається моделювання поведінки мурах, пов’язаного з їх здатністю швидко знаходити найкоротший шлях від мурашника до джерела їжі і адаптуватися до мінливих умов, знаходячи новий найкоротший шлях. При своєму русі мураха залишає на своєму шляху феромон, і ця інформація використовується іншими мурахами для вибору шляху. Це елементарне правило поведінки і визначає здатність мурах знаходити новий шлях, якщо старий виявляється недоступним. Відбувається так само моделювання збагачення шляху феромоном і його випаровування. Подані кроки алгоритму дозволяють шукати всі можливі оптимальні шляхи в просторі пошуку, а не якийсь один конкретний шлях. В незалежності від модифікації загальна ідея роботи мурашиного алгоритму може бути продемонстрована блок-схемою, наведеною на мал 2.

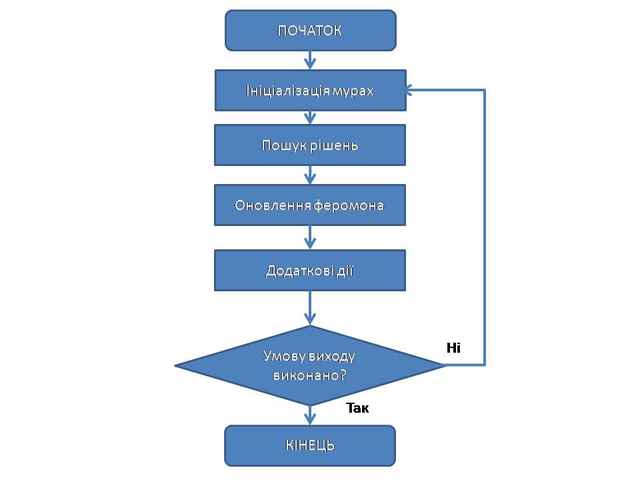
    Мал 2. Загальна схема роботи мурашиного алгоритму

    Ініціалізація мурах – стартова точка, куди вміщується мураха, залежить від обмежень, накладених умовами задачі, тому що для кожного завдання спосіб розміщення мурах є вирішальним. Або всі вони поміщаються в одну точку, або в різні з повтореннями, або без повторень. На цьому ж етапі задається початковий рівень феромону. Він ініціалізується невеликим позитивним числом для того, щоб на початковому кроці ймовірності переходу в наступну вершину не були нульовими. Імовірність переходу з вершини у вершину визначається за наступною формулою:

    ,(6)

    де э множиною можливих вершин, пов’язаних з вершиною i для мурахи k, 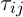– рівень феромона, – еврестична відстань, – деякі константи.

    Оновлення феромона відбувається за формулою:

    , (7)

    де – кількість мурах, – інтенсивність випаровування, – довжина шляху, побудованого k-м мурахою в момент часу t, Q – параметр значності.

    Розглянемо спосіб застосування алгоритму мурашиних колоній до сегментації зображень. У цьому алгоритмі мурахи представляються простими агентами, які випадковим чином переміщаються по дискретному масиву. Пікселі, які розсіяні в елементах масиву, можуть бути переміщені з одного елемента масиву в інший, формуючи кластери. Переміщення пікселів непрямим чином визначається поведінкою мурах. Кожна мураха може приєднувати або вилучати піксель згідно функції, яка обчислює схожість пікселя з іншими пікселями в кластері. Таким чином, мурахи динамічно кластерізіруют зображення на незалежні кластери, які включають тільки схожі між собою пікселі. Крім цього, агент представляє нові імовірнісні правила для приєднання або вилучання пікселів, а так само стратегію локального переміщення для прискорення збіжності алгоритму. Припустимо, розмірність масиву дорівнює N. Кожен елемент цього масиву пов’язаний з гніздом мурашок в певному порядку, що дозволяє мурашкам легко переходити від одного елемента до іншого. В процесі роботи алгоритму мурахи можуть змінювати, будувати або прибирати існуючі кластери пікселів. Кластер представляється сполученням двох або більше пікселів і просторово розташований в окремій ячейці масиву, що спрощує його ідентифікацію. Ініціалізували N пікселів {Р1,..., Рn} для кластеризації, розташовані в масиві таким чином, що кожен елемент масиву пов’язаний тільки з одним пікселем. Кожен мураха аi з колонії з К мурахами {a1,..., аk} приєднує випадково обраний піксель з елементів масиву і повертається в гніздо. Після початкового етапу ініціалізації відбувається етап кластеризації. Вибір мурахи проводиться випадковим чином. Він переміщається від свого гнізда до елементів масиву і визначає за допомогою імовірнісного правила приєднувати цей піксель до кластеру або ні. Кожен мураха знає список розташування пікселів, що не були приєднані іншими мурахами. Випадковим чином мураха визначає наступний піксель зі списку вільних. Цей алгоритм повторюється для кожного мурахи. Завершення алгоритму відбувається при виконанні заданого критерію зупину.

    4.3 Швидкодія

    Слід звернути увагу на той факт, що еволюційні алгоритми досить повільні. Тому, окрім основного завдання розробки еволюційного алгоритму сегментації, повинна бути вирішена проблема продуктивності. Останнього можна досягти за рахунок комбінування ресурсів CPU і GPU. Так само слід звернути увагу на той факт, що еволюційні алгоритми являють собою ряд незалежних або слабозалежних задач. Це дає високі потенційні можливості для розпаралелювання. Таким чином, об’єднуючи здатність еволюційних алгоритмів вирішувати обчислювально важкі завдання і можливості сучасних обчислювальних систем, теоретично можна домогтися високої швидкодії від повільних методів.

    Мал 3. Основні принципи побудови алгоритму

    Висновки

    Основна переслідувана мета полягає в тому, щоб побудувати добре розпаралелюваний еволюційний алгоритм, який здатний вирішити свою поставлену задачу за прийнятний час, обробляючи при цьому досить великі масиви даних, а так само комбінуючи при необхідності ресурси CPU і GPU. Легко помітити, що наявність деякого числа простих, практично незалежних один від одного агентів, дає хороші потенційні можливості для розпаралелювання алгоритму. На підставі вищевикладеного можна зробити висновок, що застосування еволюційних і ройових обчислень може допомогти усунути деякі недоліки відомих методів при обробцi тривимірних зображень. Показано, що одним з підходів може бути застосування методу кластеризації в сукупності з генетичним алгоритмом. В якості альтернативи пропонується використовувати алгоритм мурашиних колоній для вирішення задачі кластеризації, зведеної до задачі оптимізації на графах. Аналіз пропонованих рішень показав, що генетичні алгоритми і алгоритми мурашиних колоній засновані на ряді незалежних підзадач, що дозволяє значно підвищити швидкість їх роботи, виконавши розпаралелювання із застосуванням обчислень на CPU, а також GPGPU. Таким чином, напрямком подальшої роботи є розробка і реалізація паралельних обчислювальних схем для еволюційного варіанта алгоритму K-середніх і мурашиного алгоритму кластеризації зображень, а також їх перевірка на задачах кластеризації та класифікації КТ та МРТ зображень.

    Важливe зауваження

    При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення – грудень 2012 року. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

    Перелік посилань

    1. Sarang Lakare, Arie E. Kaufman. 3D Segmentation Techniques for Medical Volumes // Center for Visual Computing, Department of Computer Science, State University of New York at Stony Brook. [Электронный ресурс]. – Режим доступа: http://www.cs.sunysb.edu.
    2. Александр Вежневец, Ольга Баринова. Методы сегментации изображений: автоматическая сегментация // Компютерная графика и мультимедаи сетевой журнал. [Электронный ресурс]. – Режим доступа: http://www.cgm.computergraphics.ru.
    3. K. Krishna, M. Narasimha Murty. Genetic K-Means Algorithm // IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B: CYBERNETICS, VOL. 29, NO. 3, JUNE 1999. [Электронный ресурс]. – Режим доступа: http://eprints.iisc.ernet.in.
    4. Р.В. Дрындик, М.В. Привалов. Применение эволюционных вычисления для сегментации трехмерных медицинских изображений/ Сборник материалов к III Всеукраинской научно-технической конференции студентов, аспирантов и молодых ученых. – Донецк, ДонНТУ – 2012, с. 480 – 484.
    5. D. Goldberg. Genetic Algorithms in Search, Optimization and Machine Learning. Reading, MA: Addison-Wesley, 1989.
    6. C. von der Malsburg. The correlation theory of brain function. Technical report, Max-Planck-Institute Biophysical Chemestry, 1981.
    7. G.P. Babu and M.N. Murty. "Simulated annealing for selecting initial seeds in the K-means algorithm" Ind. J. Pure Appl. Math., vol. 25, pp. 85–94, 1994.
    8. J.N. Bhuyan, V.V. Raghavan, and V.K. Elayavalli. "Genetic algorithm for clustering with an ordered representation" in Proc. 4th Int. Conf. Genetic Algorithms. San Mateo, CA: Morgan Kaufman, 1991.
    9. D.R. Jones and M.A. Beltramo "Solving partitioning problems with genetic algorithms" in Proc. 4th Int. Conf. Genetic Algorithms. San Mateo, CA: Morgan Kaufman, 1991.
    10. G.P. Babu and M.N. Murty. "A near-optimal initial seed selection in K-means algorithm using a genetic algorithm" Pattern Recognit. Lett., vol. 14, pp. 763–769, 1993.
    11. G.P. Babu. "Connectionist and evolutionary approaches for pattern clustering" Ph.D. dissertation, Dept. Comput. Sci. Automat., Indian Inst. Sci., Bangalore, Apr. 1994.
    12. G. Rudolph. "Convergence analysis of canonical genetic algorithms" IEEE Trans. Neural Networks, vol. 5, no. 1, pp. 96 – 101, 1994.
    13. L. Davis, Ed., Handbook of Genetic Algorithms. New York: Van Nostrand Reinhold, 1991.
    14. H. Spath, Clustering Analysis Algorithms. New York: Wiley, 1980.
    15. Y.T. Chien. Interactive Pattern Recognition. New York: Marcel-Dekker, 1978.