Економіко-матиматичне моделювання ціноутворення на ринку кабельної продукції із застосуванням павутинних моделей

Зміст

• Вступ
• 1. Актуальність теми
• 2. Мета і задачі дослідження та заплановані результати
• 3. Огляд досліджень та розробок
• 4. Розробка павутинної моделі динаміки цін на мідь
• Висновки
• Перелік посилань

Вступ

На даний момент підвищився інтерес до моделей знаходження рівноваги в задачах «попит-пропозиція», так як нестабільність українського ринку підвищує інтерес підприємців до поведінки цін на товар при зміні обсягів виробництва. Взаємодія, яка складається на ринку, між попитом і пропозицією призводить до поняття рівноваги. Рівновага – це ситуація на ринку, при якій обсяг попиту і обсяг пропозиції рівні. Для знаходження рівноваги можна використовувати різні моделі, але на сучасному етапі часто використовується павутинні моделі.

1. Актуальність теми

На даний час актуальність набувають моделі знаходження рівноваги в задачах попит-пропозиція. Класична павутинна модель відноситься до такого класу, вона застосовується як у стабільних, так і не стабільних умовах. Павутинна модель дає можливість для більш ефективної адаптації підприємствами до ринкових умов, тому в даний час дана модель цікава для досліджень. На практиці дані моделі допомагають визначати і прогнозувати поведінку цін на товар, що допомагає приймати рішення і давати рекомендації до поведінки фірми на ринку при певних умовах.

2. Мета і задачі дослідження та заплановані результати

На даний час актуальність набувають моделі знаходження рівноваги в задачах попит-пропозиція. Класична павутинна модель відноситься до такого класу, вона застосовується як у стабільних, так і не стабільних умовах. Павутинна модель дає можливість для більш ефективної адаптації підприємствами до ринкових умов, тому в даний час дана модель цікава для досліджень. На практиці дані моделі допомагають визначати і прогнозувати поведінку цін на товар, що допомагає приймати рішення і давати рекомендації до поведінки фірми на ринку при певних умовах.

3. Огляд досліджень та розробок

Загальна економічна рівновага бере свій початок ще в роботах економістів-класиків. Вперше ідея про загальну рівновагу була висловлена Л. Вальрасом, потім даною темою займався Маршалл [3] і економіст П'єро Сраффа [4]. На сучасному етапі павутинна модель має великий інтерес. У другій половині ХХ століття були вивчені властивості даної моделі Р. Алленом [5]. Потім ці дослідження були продовжені такими вченими – О. Ланге [6], С. Біром [7] та іншими. На сучасному етапі в розробці павутинної моделі найбільш відомими вченими є: C. Chiarella [8], C.H. Hommes [9–10], A. Matsumoto [11] та інші. Серед національних джерел можна виділити Шевченко В.В. [12], Боровська Т.М. [13], Моспан А.А. [14–15] та інші.

Зауважимо, що серед національних джерел, знайдено дуже мало робіт з даної тематики. Однією із знайдених робіт є робота Шевченко В.В. – Использование паутинообразной модели при принятии перспективных решений. У даній роботі автор проводить класифікацію підходів щодо прогнозування рівноваги ринкових цін. Також автор розглядає 3 можливих стану ринку, залежно від характеристик ліній попиту і пропозиції. Автор розглядає, в яких випадках на практиці необхідно використовувати павутинну модель. Також у статті розглянуті основні недоліки та переваги павутинної моделі, також наведені математичні розрахунки даної моделі в формульному вигляді.

Наступною роботою є робота Борівської Т.М. – Моделювання і оптимізація процесів розвитку виробничих систем з урахуванням використання зовнішніх ресурсів та ефектів освоєння. У своїй роботі автор узагальнив функції попиту та пропозиції в павутинної моделі. У статті вводитися функція як параметризована логічна залежність, а також задається узагальнення функцію виробництва. Місткість ринку є головним обмеженням в побудованій моделі.

Наступними роботами є роботи Моспан А.А., Назарова І.А. – Реализация паутинообразных моделей динамики цен на основе программного пакета E&F Chaos, Моделирование динамики рыночных цен на базе нелинейной паутинообразной модели ценообразования. У даних роботах розглянуті кілька видів павутинної моделі ціноутворення для дослідження динаміки ринкових цін. Наведено приклад побудови та дослідження моделі за допомогою програми E & F Chaos, яка дозволяє більш детально вивчити процеси утворення цін і досягнення оптимальної рівноважної ціни; представити графічно зміни цін, поведінка цінової функції; передбачити хаотичний процес цін; бути корисною підставою для складання якісних рекомендацій для основних гравців ринку [14–15].

Інша справа із закордонними джерелами. Павутинна модель і її різні модифікації становить значний інтерес для всього світу. Значний внесок у дослідження павутинної моделі зробив професор в економічній динаміці Cars Hommes, який написав величезну кількість праць з досліджень павутинної моделі, так само він розробив різні види павутинних моделей. Так само із зарубіжних джерел можна бачити, що були побудовані павутинні моделі для різних ринків, наприклад японськими дослідниками – для ринку сільськогосподарської продукції, китайськими та корейськими дослідниками – для ринків майна та ін. Так само значний внесок зробили вчені Paul Bedford і Chris Bloor вони побудували павутинну модель для фінансової стабілізації в Новій Зеландії [16].

4. Розробка павутинної моделі динаміки цін на мідь

Дослідження процесу ціноутворення на мідь розглянуто на прикладі підприємства ПАТ Донбаскабель, яке є одним з найбільших підприємств з виробництва кабельно-провідникової продукції. Це сучасне, яке динамічно розвивається підприємство, яке оснащено високотехнологічним обладнанням. Підприємство виробляє більше 100 видів кабельно-провідникової продукції – номенклатура налічує понад дві тисячі маркорозмірів. ПАТ Донбаскабель є постачальником кабельно-провідникової продукції на багатьох підприємств Міністерства транспорту, вугільної, енергетичної, нафтохімічної галузі та гірничо-металургійного комплексу. Підприємство акредитоване як корпоративний постачальник ДП НАЕК Енергоатом.

Дане підприємство займається випуском кабельно-провідникової продукції двох типів, що містять алюмінієві або мідні жили. У доповіді наведено результати моделювання ціноутворення для кабельно-провідникової продукції з мідними жилами. Розглядається попит і пропозиція на мідь, залежно від цього буде змінюватися і попит і пропозиція на мідну кабельно-провідникову продукцію, так як мідь є основною складовою даної продукції і займає значну частину в собівартості продукції.

Павутинна модель ринку – модель, що зображує траєкторію руху до стану рівноваги, коли реакція пропозиції або попиту запізнюється.[1]

Введемо наступні позначення, нехай p – ціна товару, d – обсяг попиту, s – пропозиція. Передбачається, що d(p) і s(p) є безперервними функціями, при цьому, якщо ціна p – мала, то d(p)-s(p)>0 (попит перевищує пропозицію), а при великих цінах d(p)-s(p)<0 і пропозиція перевищує попит. При даних припущення існує рівноважна ціна p*, яка задовольнить рівнянню d(p*)=s(p*) [2].

Павутинна модель ринку з математичної точки зору – рішення рівняння (1).

При побудові павутинної моделі з метою моделювання процесу ціноутворення для ринку міді використовувалися дані ПАТ Донбаскабель. Першим етапом дослідження є побудова регресійних моделей попиту і пропозиції на продукцію, як функцій ціни на мідь. Лінійні парні економетричні моделі для функцій попиту і пропозиції в умовах одного виробника розроблені з використанням методу найменших квадратів в пакеті EXCEL та наведені на рис. 2–3.

Припустимо, виробники визначають величину обсягу виробництва (пропозиція обсягу товару) в поточному році на основі цін, що встановилися в попередньому періоді. Наприклад, кількість мідної катанки, для виробництва кабельної продукції, вибирають в залежності від ціни, що склалася в попередньому році. Таким чином, у функції пропозиції повинен бути врахований часовий лаг тривалістю в одиницю часу (в даному випадку місяць). Дійсно, пропозиція з'явиться на ринку після закінчення даного циклу, тобто, через місяць після прийняття рішення [2].

Згідно з даними припущеннями опишемо динаміку ціни рівняннями (2) [2].

Справедлива наступна рівність:

Проілюструємо застосування даного підходу на конкретних прикладах. Нехай тепер задана функція (4).

де c>0, e>0 – задані параметри, такі, що існує рівноважна ціна p*. Виходячи з цього прикладу, попит на мідь буде представлений наступним рівнянням:

Припустимо, що s(p)=a+b*p. Тоді пропозиція на мідь буде мати вигляд (6).

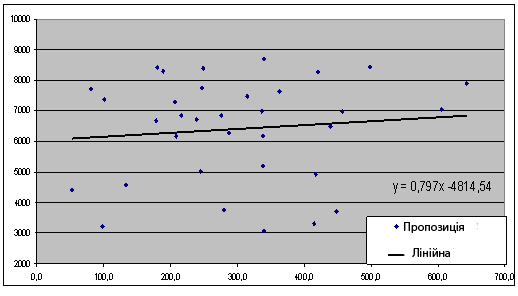
Побудуємо графік попиту і пропозиції на мідь рис. 4.

Рівновага досягається в точці: p=6086 $ за тонну, Q=35,9 тонн.

Можливі випадки:

1. Якщо |l|<1 то справедливо рівняння (7):

де l=b/e. В цьому випадку рівновага є стійкою [2].

2. При |l|=1 отримуємо (8-9):

Тут значення q(i) чергуються навколо рівноважного стану.

3. Якщо |l|>1 то {q(n)} розходиться і рівновага не є стійкою. У нашому випадку (10):

|l|>1 – це означає, що {q(n)} розходиться і рівновага не є стійкою. Це означає, що при зміні цін і обсягу попиту та пропозиції буде встановлюватися нова рівновага.

Висновки

Виходячи з досліджень, при побудові павутинна модель буде розходитися, так як рівновага є нестійкою. Нестійка рівновага означає, що при зміні цін на мідь і обсягу попиту та пропозиції на мідь буде встановлюватися нова рівновага, що означає, що буде встановлюватися нова рівноважна ціна і рівноважний попит і пропозиція.

На даний момент вивчення в області павутинної моделі пішло далеко вперед. Дана модель допомагає вивчити внутрішній механізм ціноутворення, визначити параметри, які впливають на систему, а також проаналізувати систему і дати рекомендації з поведінки в даній системі. Павутинна модель є складним апаратом, що дозволяє дати пояснення процесу зміни ціни, а також дозволяє визначити систему управління цінами ринку.

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.

Перелік посилань

1. Beчкaнoв Г.C., Beчкaнoвa Г.P. Паутинообразная модель [Электронный ресурс] – Режим доступа: http://www.inventech.ru
2. Коврижных А. Ю., Конончук Е. А., Лузина Г. Е. Методы вычислений в экономическом моделировании // Учебно-методическое пособие – Екатеринбург 2008– 231с.
3. Маршалл А. Принципы экономической науки, М.: Прогресс, 1993.
4. Сраффа П. Производство товаров по средством товаров.
5. Ален Р. Математическая экономия: Пер. с англ. – М.: Из-во иностр. Литературы, 1963 – 667 с.
6. Ланге О. Оптимальные решения ndash; М.:Прогресс, 1967 – 286 с.
7. Бир С. Киберенетика и управление производством ndash; М.:Наука, 1965 – 388 с.
8. Chiarella C., Xue-Zhong He, Peiyuan Zhu Fading memory learning in the cobweb model with risk averse heterogeneous producers // School of Finance and Economics. ndash; Australia, 2003 – 45 p.
9. Hommes C.H. Heterogeneous agent models in economics and finance // University of Amsterdam, Tinbergen Institute, CeNDEF, – Amsterdam, 2005 – 70 p.
10. Diks C., Hommes C., Panchenko V., Roy van der Weide E&F Chaos: A User Friendly Software Package for Nonlinear Economic Dynamics, Amsterdam, 2008 – 26 p.
11. Matsumoto A. Ergodic Cobweb Chaos // Discrete Dynamics in Nature and Society, Niigata University – Japan, 1996, Vol. 1, p. 135–146
12. Шевченко В.В. Использование паутинообразной модели для принятия перспективных решений // Наукові праці ДонНТУ, Серія економічна, Випуск 87, с. 142–146
13. Боровская Т.М. Моделювання і оптимізація процесів розвитку виробничих систем з урахуванням використання зовнішніх ресурсів та ефектів освоєння // Монографія. – Вінниця, 2009, с. 36–46.
14. Моспан А.А., Назарова И.А. Реализация паутинообразных моделей динамики цен на основе программного пакета E&F Chaos // Информационные управляющие системы и компьютерный мониторинг – Донецк, ДонНТУ–2010
15. Моспан А.А., Назарова И.А. Моделирование динамики рыночных цен на базе нелинейной паутинообразной модели ценообразования // Тезисы IV Международной научно-практичной конференции молодых ученых, аспирантов, студентов Современная информационная Украина: информатика, экономика, философия, Том II, г. Донецк, стр. 210 – 214
16. Bedford P., Bloor C. A cobweb model of financial stability in New Zealand // Discussion Paper Series, – New Zealand, 2009 – 22 p.