Реферат за темою випускної роботи

1. Дослідження існуючих форматів представлення чисел з плаваючою комою та їхніх особливостей

2. Дослідження способів представлення дійсних чисел і розробка перетворювача мантиси числа

3. Програмна модель постбінарнх форматів

4. Структура програмної моделі PBinary

5. Розробка перетворювача чисел на ПЛІС

Перелік посилань

Вступ

         На сьогоднішній день апаратне забезпечення комп'ютерів в змозі проводити всілякі обчислення з числами, які можуть бути представлені лише у двох форматах - цілі числа і числа з плаваючою комою. Цілочислена арифметика оперує кінцевою підмножиною множини цілих чисел. Якщо апаратна частина справна, а програми не містять помилок, то цілочислена арифметика і програмні надбудови над нею працюють без похибок. Наприклад, на основі цілочисленої арифметики можна побудувати арифметику систематичних дробів довільної розрядності і звичайних дробів.Для точного представлення результатів арифметичних операцій, сучасний комп'ютер має можливість зберігати необхідну кількість розрядів, для точного уявлення будь-якого великого цілого числа. А дробові числа в комп'ютері представлені в форматі з плаваючою комою. У загальному випадку такий формат подання чисел є оптимальним з точки зору витрат пам'яті та процесорного часу, на роботу з числами і точності обчислень. Але так як він спочатку містить в собі деяку похибку, то для точних наукових, і важливих виробничих обчислень його похибка часто стає неприпустимо високою.Метою даної роботи є дослідження недоліків сучасних способів і форматів представлення дробових чисел у пам'яті комп'ютера і підвищення точності цих стандартів, шляхом розробки модифікованих форматів, розробка програмної та апаратної моделі перетворення чисел в нові формати.

1.Дослідження існуючих форматів представлення чисел з плаваючою комою та їхніх особливостей

         В даний час одним з перспективних наукових напрямків в галузі обчислювальної техніки є проектування спеціалізованих процесорних пристроїв з малим енергоспоживанням. При впровадженні нових архітектур з'являється необхідність нарощування обсягу системного програмного забезпечення, важливу частину якого складають математичні бібліотеки, що включають в себе операції з плаваючою комою. При цьому основною проблемою є те, що арифметика з плаваючою комою повинна мати властивості математичної коректності. На апаратному рівні дана проблема може бути вирішена шляхом відповідності стандартам обчислень з плаваючою комою.У світлі вищевикладеного представляються актуальними задачі проектування, розробки та реалізації базових математичних алгоритмів нижнього рівня, наприклад, елементарних арифметичних функцій для вбудовуваної процесорної системи. На початковому етапі проектування повинна бути вирішена найважливіша задача, пов'язана із забезпеченням коректності обчислень, тобто отримання результату з гарантованою точністю. Рішення такого завдання можна розбити на два етапи: 1-й етап - модифікація форматів представлення дійсних чисел (коректність подання даних); 2-й етап - введення додаткових методів контролю точності для стандартних обчислювальних алгоритмів (корекція обчислень). У даній роботі показана реалізація 1-го етапу, в ході якої пропонується відхід від традиційного (бінарного) подання дійсних чисел в ЕОМ в сторону постбінарного. При такому поданні чисел з плаваючою комою запропоновано ряд модифікованих форматів[2, 3, 5], здатних представляти не тільки числа з плаваючою комою, а й їхні сукупності у вигляді звичайних дробів (пара чисел - чисельник і знаменник) і інтервалів (пара чисел - межі інтервалу).Для подальшої перевірки алгоритмів арифметичних і логічних операцій над постбінарними числами виникла необхідність розробки програмної моделі відповідних форматів. При цьому апарат введення чисел має бути настільки гнучким, щоб була можливість подання будь-якого точного відображення множини всіх дійсних чисел, тобто перетворення вхідне число х → постбінарний формат (pbinary [x]) і pbinary [x] → вихідне число y повинне бути максимально точним і прямую до рівності х = y.В результаті пошуку програмних продуктів, що працюють з числами довільної довжини, було виявлено: всі програмні моделі представлення чисел в двійковій системі числення (зокрема, дійсних чисел) мають обмеження на кількість знаків після коми і неможливість подання вхідних чисел і результатів в експоненційному вигляді. На тлі інших додатків істотно виділяється безкоштовна програма IEEE754 v.1.0[4], яка здатна виконувати перетворення дійсних чисел у формат одинарної або подвійної точності стандарту IEEE-754 в обох напрямках. Програма відображає абсолютно точні значення десяткових або двійкових чисел, може представляти вихідні числа і результати перетворення в експоненційному вигляді і дозволяє вводити вихідне десяткове число до 1074 значущих цифр у простому або експоненційному вигляді. Даний програмний продукт був обраний в якості прототипу до побудови представленої далі моделі перетворення десяткового дійсного числа довільної точності в постбінарні формати різної точності.

2. Дослідження способів представлення дійсних чисел і розробка перетворювача мантиси числа

         В роботі [4] було запропоновано різні способи для подолання проблем, пов'язаних з обмеженням розрядності чисел, оскільки використання при обчисленнях розрядності, істотно перевищує стандартну, є одним із способів отримання правильних результатів. Всі ці способи в сукупності дозволяють в процесі обчислень виконувати наступні операції:

- Збільшення (або вирівнювання) розрядності щоб уникнути переповнення порядку результату і виконання коректних обчислень;

- Виконання так званого відкладеного розподілу, коли окремо обчислюються чисельник і знаменник, а ділення проводиться на останньому кроці обчислення;

- Використання інтервальних обчислень.

Рисунок 2.1 - Запропоновані варіанти модифікованих форматів чисел з плаваючою комою, для 128-розрядного числа (S, P, M - знак, порядок і мантиса числа, MF, CF - модифікатор і формат числа, n - покажчик)

 

Рисунок 2.2 - Запропоновані варіанти модифікованих форматів постбінарних чисел з плаваючою комою, для 128-розрядного числа (S, P, M - знак, порядок і мантиса числа, MF, CF - модифікатор і формат числа, n - покажчик)

 

Рисунок 2.3 - Запропоновані варіанти модифікованих форматів постбінарних чисел з плаваючою комою, для 256-розрядного числа.

 

3. Програмна модель постбінарнх форматів

         В сучасних обчислювальних пристроях для подання дійсних чисел використовуються формати, відповідні стандарту IEEE754-2008, які складаються з полів знака, порядку та мантиси числа. Така ж структура збережена і в постбінарних форматах, однак поле мантиси зазнало модифікації, виділивши незначну кількість розрядів на поле ідентифікатора [3, 5]. Програмна модель PBinary є перетворювачем вихідного десяткового числа в двійкове, «упаковане» в постбінарних форматах. PBinary реалізовано мовою Java і займає близько 300 КБ дискового простору. Створення моделі PBinary у вигляді Java-програми було обгрунтовано, по-перше, кросплатформеністю, і, по-друге, підвищеною швидкодією виконання елементарних математичних операцій. Інтерфейс програми PBinary представлений на рис. 4.1. У полі введення даних формується вихідне десяткове число, яке може вводитися з клавіатури або завантажуватися з текстового файлу. Перемикачі «число», «дріб» і «інтервал» дозволяють представляти вхідні дані у вигляді одного числа, чисельника і знаменника дробу або меж інтервалу. Прапорець «тетракод» дозволяє відображати значення полів форматів в тетракоде, де кожна пара двійкових біт представляє значення тетріта t∈{0, 1, A, M}[8] наступним чином: 00 для «А», 01 для «0», 10 для «1» і 11 для «М». Цифровий лічильник показує кількість значущих цифр вхідного числа (в простому або експоненційному вигляді) яке буде враховуватися при подальшому перетворенні (за замовчуванням - 1024 цифри). Кнопки «Старт» і «Скинути в 0» дозволяють почати перетворення або скинути отримані раніше результати. Результати всіх перетворень, що виконуються моделлю PBinary записуються в інформаційні поля групи вкладок «pbinary32-pbinary256». Назви вкладок «pbinary32-pbinary256» повторюють назви відповідних постбінарних форматів різної точності. Тіло кожної вкладки містить наступні інформаційні поля:

  1. Значення полів числа. Дане поле містить інформацію про структуру формату (рис. 2), назви та значення його полів (використовується 2 с/с і 16 с/с), належності числа до стандартної множини (± нормалізоване, ± денормалізованное, ±∞, не число (NaN)) і вибраному способі округлення (в меню «Опції») при формуванні значень полів формату (до нуля (без округлення), до найближчого цілого, до +∞ і до -∞). Дане поле відображає результат перетворення х → pbinary [x].

 

Рисунок 3.1 - Інтерфейс програми PBinary

  2. Значення, отримані з pbinary - точні значення у вигляді дійсного числа з фіксованою крапкою, отримані в десятковому або двійковому вигляді при «розпакуванні» полів поточного формату pbinary. Отримане значення можна відобразити в простому (рис. 3, а) і експоненційному (рис. 3, б) вигляді. Варто зазначити, що такі точні обчислення мікропроцесор виробляти не здатний, тому PBinary не використовує математичних можливостей мікропроцесора, а імітує математичні розрахунки виконувані вручну. Дане поле відображає результат перетворення pbinary [x] →  y.

  3. Похибка. У цьому полі обчислюється абсолютна похибка подання вихідного числа в постбінарном форматі. Значення похибки дозволяє оцінити точність представлення вихідного числа і вибрати оптимальну точність (від 32 до 256 двійкових розрядів) для його зберігання. Дане поле показує, наскільки точна рівність х = y.

Рисунок 3.2 - Представлення полів формату pbinary128

         В поле статусу вікна програми виводиться інформація про час перетворення, яке визначає часовий інтервал з моменту натискання на кнопку «Старт» і до заповнення всіх інформаційних полів. Слід зазначити, що при проведенні численних експериментів з різними вхідними числами (і з різною кількістю значущих цифр у числі) в межах показника експоненти -1000...1000, час перетворення ні разу не перевищила 15-секундний рубіж.

Рисунок 3.3 - Точне значення числа в 10 с / с, отримане з формату pbinary128, в простому (а) і експоненційному (б) вигляді

4. Структура програмної моделі PBinary

         Основу моделі PBinary складають функції реверсивного перетворення чисел десяткової і двійковій систем числення. Відомі алгоритми таких перетворень в даній концепції незастосовні, оскільки:

1) вихідне десяткове дробове число неможливо точно уявити ні в одному із стандартних форматів дійсних чисел, т. я. десяткова дріб х₁₀ записується у вигляді рядка цифр a_k (0 ≤a_k ≤9) з кількістю n розрядів цілої частини і m розрядів дробової частини числа. (1)

За замовчуванням вихідна десяткова дріб може бути представлена значенням n + m = 1024, проте цю суму можна збільшити до 10 000. Такі числа в регістрах сучасних мікропроцесорів не можуть бути представлені.

2) при перетворенні десяткового дробу в двійковий виникає необхідність представлення раціонального числа х₁₀ в х₂ у вигляді лінійної комбінації (у більшості випадків нескінченної) ступенів числа 2: , (2)

де b_k і c_k - цифри цілої частини і дробової частини (b_k, c_k ∈{0, 1}), n - число розрядів цілої частини. При великих значеннях n (наприклад, у форматі pbinary256 довжина мантиси дорівнює 219 розрядам) не представляється можливим завантажити таке число в регістри сучасного мікропроцесора. Для подолання цієї ситуації було прийнято рішення зберігати всі числові значення в строкових форматах та розробити власні алгоритми, що імітують для перетворення 2↔10 с/с додавання, віднімання, множення і ділення «у стовпчик» строкових чисел. При цьому кожна двійкова і десяткова цифра, знаки «+», «-», «,» і «е» є символами системи Юнікод. Даний підхід дозволив уявити числа у вигляді рядків великої довжини (до 4 ГБ (для платформи Java), де кожен символ рядка дорівнює двом байтам), тобто фактично модель PBinary в змозі враховувати до 2 • 10⁹ значущих цифр вхідного числа. Всі операції, що відбуваються після початку перетворення (натискання кнопки «Старт») можна розбити на кілька етапів (рис. 4.1):

Рисунок 4.1 - Етапи роботи конвертору (4 кадри, тривалістю 2 с., 7 повторів, розмір — 62 КБ.)

Етап 1. Інкапсуляція вхідних даних. Якщо вхідна строкове число представлене в нормалізованому вигляді, то воно приводиться до простого, що складається з цифр, знакового символу («+» або «-») та роздільника «,». Символ знака визначає знаковий розряд форматів, а модуль числа розбивається на дві частини, що представляють рядковий еквівалент цілої і дробової частини вхідного числа.

Етап 2. Отримання двійкового числа і заповнення полів постбінарних форматів («упаковка» числа). Функція перетворення 10↔2 с/с реалізує два алгоритми, які виконують перетворення цілої і дробової частини строкового числа. На цьому етапі дробова частина двійкового числа може виявитися нескінченною, аналогічної (2). У цьому випадку обчислення відбувається до кількості двійкових розрядів, необхідних для коректного заповнення мантиси старшого формату (в даному випадку pbinary256). Якщо відбувається перетворення вхідного раціонального числа, яке можна представити у вигляді (де q і m - цілі числа), то таке число має кінцевої записом у двійковій системі числення: , (3) де і представляють двійкові записи відповідно приватного і залишку від ділення q на 2m. Якщо значення n + m виявиться менше розрядності мантиси більшого постбінарного формату (в даному випадку pbinary256), відсутні розряди заповнюються незначущими нулями.

Отримані частини вже двійкового числа знову збираються в дробовий формат і нормалізуються. Для кожного формату pbinary розраховуються значення порядку зі зміщенням, відпрацьовується механізм встановленого округлення мантиси. Отримані значення записуються у відповідні поля форматів.

Етап 3. «Розпакування» числа з форматів для отримання точного значення. З значень полів кожного постбінарного формату формується точне двійкове число в нормальному вигляді. Для цього до значення мантиси зі знаком додається старша «1» (якщо число належить до області нормалізованих чисел), обчислюється значення експоненти без зміщення, визначаючи тим самим положення коми, що ділить поле мантиси на цілу і дробову частини. Далі отримане в нормальному вигляді двійкове число перетворюється в точне десяткове. Обидва ці числа можна відобразити у відповідному інформаційному полі (рис. 3) у нормальному і експоненційному вигляді.

Етап 4. Обчислення похибки подання. Абсолютна похибка представлення чисел D являє собою різницю між вихідним десятковим числом x і отриманим точним десятковим числом y з полів форматів після перетворення: D = x - y. Значення D виводиться окремо для кожного формату і дозволяє перевірити ефективність використання постбінарних форматів різної точності для заданого числа.

Оскільки модель PBinary не працює з числами, а тільки з їх строковими еквівалентами, то описані вище математичні операції також проводяться з рядковими типами даних. У таких випадках кожен символ рядка представляє цифру певного розряду числа, і реалізація всіх математичних алгоритмів зводиться до імітації роботи однобітних суматора і дільника.

4.2 Дослідження часових характеристик

         Для дослідження часових характеристик перетворювача, обрано ряд чисел, які подавалися на вхід програми. Принцип перевірки часу виконання програми був заснований на вимірі системного часу в момент натискання кнопки «старт», до закінчення всіх перетворень. Результати дослідження представлені на рис. 4.2, де по осі ординат вказано час виконання програми в мілісекундах, а по осі абсцис - значення експоненти для кожного числа. Тестування проводилося на комп'ютері з наступними параметрами: CPU: Celeron M 1.6 GHz, RAM: 1024 MB, HDD: SATA 80026 MB.

Рисунок 4.2 - Тимчасова діаграма перетворювача (вісь ординат - тривалість роботи в секуднах, вісь абсцис - довжина числа)

         За результатами дослідження виявлено, що при невеликих значеннях експоненти, час роботи залежить від кількості значущих цифр самого числа, а при великих значеннях експоненти різниця між вихідними числами не істотна. Аналізуючи отримані результати можна припустити, що при негативних значеннях експоненти, залежність часу від її величини лінійна, а при позитивних значеннях - експоненціальна. Це явище можна пояснити наступним: при негативних значеннях експоненти відбувається багаторазове виконання операції множення (фактично, багаторазове складання), а при позитивних значеннях експоненти - багаторазові операції ділення (фактично, багаторазове віднімання).

5. Розробка перетворювача чисел на ПЛІС

         Кінцевим етапом роботи є розробка постбінарного процесора, для реалізації на ПЛІС, так як виготовлення замовних БІС є дуже дорогим і трудомістким. Розроблено модель даного пристрою на мові HDL, яка дозволяє перетворювати вхідне число в постбінарний формат, для подальшої роботи, так як даному процесорі всі операції виконуються над постбінарнимі числами.

RB0 і RB1 - буферні регістри.

B2PT - перетворювач бінарних чисел в постбінарні

P2BT - перетворювач постбінарних чисел в бінарні

ALU - арифметико-логічний пристрій (АЛП)

RFL - регістр прапорів

RB0 служить для введення вихідного числа. Розрядність - 64 біта.

B2PT перетворює вхідний число з буфера RB0 в формат, необхідний для подання в АЛП, визначає код формату і модифікатор формату для вхідного числа.

В RFL зберігаються код і модифікатор числа, його тип (бінарний або постбінарний), коди помилки. Дані з регістра прапорів використовуються при роботі АЛУ, а також для перетворення вихідних чисел.

 P2BT - перетворює вхідне 128-бітове число результату з АЛУ в бінарний формат, і записує його в регістри RB0 і RB1. При цьому аналізується значення поле формату числа, і якщо його можна представити 64 бітами, то запис відбувається тільки в регістр RB0, а RB1 заповнюється нулями.

 

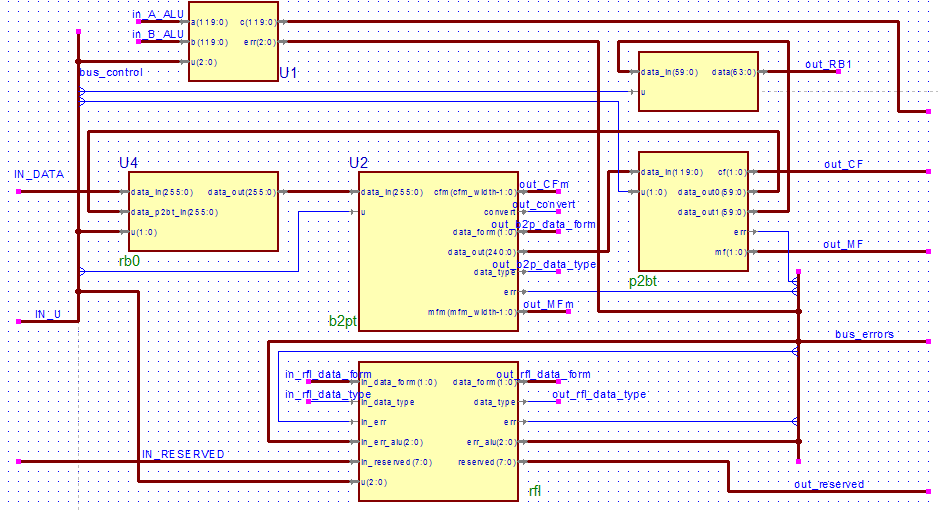
Рисунок 5 - Структурна схема розробленого пристрою

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.

Перелік посилань

1. Hammer R., Hocks M., Kulisch U., Ratz D. — Numerical Toolbox for Verified Computing (Pascal-XSC Programs) Springer-Verlag Berlin Heidelberg, 1993, с.8.

2. Аноприенко А.Я., Гранковский В.А., Иваница С.В. Пример Румпа в контексте традиционных, интервальных и постбинарных вычислений // Научные труды Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП-2011). Выпуск 9 (179): Донецк: ДонНТУ, 2011. С. 324–343.

3. Аноприенко А.Я., Иваница С.В., Кулибаба С.В. Особенности представления постбинарных вещественных чисел в контексте интервальных вычислений и развития аппаратного обеспечения средств компьютерного моделирования // Моделирование и компьютерная графика / Материалы IV международной научно-технической конференции – 5-8 октября 2011 г. Донецк, ДонНТУ. – 2011. С. 13-19.

4. Бесплатные программы SoftElectro. Программа IEEE754 — конвертор чисел формата IEEE754 c абсолютной точностью представления результата. Электронный ресурс. Страница доступа: http://www.softelectro.ru/program.html.

5. Аноприенко А.Я., Иваница С.В. Постбинарный компьютинг и интервальные вычисления в контексте кодо-логической эволюции. — Донецк, ДонНТУ, УНИТЕХ, 2011. — 244 с.

6. Loh E., Walster G. Rump’s Example Revisited // Reliable Computing 8: 2002, p. 245–248.

7. Петров Ю.П. Обеспечение надежности и достоверности компьютерных расчетов. — СПб: БХВ-Петербург, 2008. — 160 с.

8. Аноприенко А.Я. Обобщенный кодо-логический базис в вычислительном моделировании и представлении знаний: эволюция идеи и перспективы развития // Научные труды Донецкого национального технического университета. Серия «Информатика, кибернетика и вычислительная техника» (ИКВТ-2005) выпуск 93: – Донецк: ДонНТУ, 2005. C. 289-316.

9. Аноприенко А.Я., Иваница С.В. Особенности постбинарного кодирования на примере интервального представления результатов вычислений по формуле Бэйли-Боруэйна-Плаффа // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ-2010). Выпуск 11 (164). – Донецк: ДонНТУ, 2010. С. 19-23.

10. Аноприенко А.Я., Иваница С.В. Интервальные вычисления и перспективы их развития в контексте кодо-логической эволюции // Научные труды Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП-2010). Выпуск 8 (168): Донецк: ДонНТУ, 2010. С. 150–160.

11. Moore R.E. Interval analysis. Eiiglewood Cliffs / R.E. Moore — N.J.:Prentic-e-llall, 1966.

12. Иваница С.В., Аноприенко А.Я. Особенности реализации операций тетралогики // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ-2011). Выпуск 13 (185). – Донецк: ДонНТУ, 2011. С. 134-140.

13. IEEE Standard for Floating-Point Arithmetic (IEEE 754) http://en.wikipedia.org/wiki/IEEE_754-2008