


Геоінформаційна система призначена для збору, зберігання, аналізу та графічної візуалізації просторових даних і пов’язаної з ними інформації про представлені в ГІС об’єктах. Термін також використовується в більш вузькому сенсі — ГІС як інструмент (програмний продукт), що дозволяє користувачам шукати, аналізувати і редагувати цифрові карти, а також додаткову інформацію про об’єкти.
Але, з ростом обсягу даних, що зберігаються в Інтернеті, виникли проблеми візуалізації великого обсягу просторових даних.
У наш час, найбільш поширеною геоінформаційної системою є Google Maps. Але і в цій системі існують свої проблеми з відображенням великої кількості просторових даних. Відображення геоінформаційних даних може зайняти велику кількість часу — навіть для високошвидкісного Інтернету такі операції можуть стати серйозним випробуванням, не кажучи вже про швидкість підключення у середньостатистичного користувача. Одним з рішень даної проблеми є кластеризація.
На даний момент існує велика кількість методів кластеризації, що використовують різні заходи і міри. Але, незважаючи на це, проблема актуальна, розробляються нові алгоритми та підходи. Дана проблема досить складна, тому повністю не вирішена, тому що для кожного завдання необхідно вибрати відповідний алгоритм і міри відстаней. Вибір метрики повністю лежить на досліднику, оскільки результати кластеризації можуть істотно відрізнятися при використанні різних заходів.
У наш час розробки в області кластеризації просторових даних засобами Google Maps практично не ведуться. Так як для цього існують стандартні функції Google Maps API. Але на практиці стандартні засоби кластеризації не відповідають поставленим вимогам. Візуалізація великої кількості просторових даних займає тривалий час.
Дана проблема вирішиться за допомогою вибору більш підходящого методу кластеризації, що дозволить багато в чому поліпшити процес відображення просторових даних і полегшить роботу з ними.
В процесі роботи над дипломною роботою планується проаналізувати методи і алгоритми кластеризації, розібратися в області застосування кожного з них і вибрати найбільш підходящий для даного завдання. Результатом роботи буде інформаційна система, яка буде вирішувати завдання візуалізації великої кількості просторових даних швидше, ніж стандартні засоби Google Maps.
Кластеризація (або кластерний аналіз) — це задача розбиття множини об’єктів на групи, звані кластерами. Усередині кожної групи повинні виявитися "схожі" об’єкти, а об’єкти різних груп повинні бути відмінні один від одного. Головна відміна кластеризації від класифікації полягає в тому, що перелік груп чітко не заданий і визначається в процесі роботи алгоритму[4].
Кластерний аналіз виконує такі основні завдання:
Незалежно від предмета вивчення, застосування кластерного аналізу припускає наступні етапи:
Кластерний аналіз пред’являє наступні вимоги до даних:
Після отримання та аналізу результатів можливе корегування обраної метрики і методу кластеризації до отримання оптимального результату.
Цілі кластеризації:
У першому випадку число кластерів намагаються зробити поменше. У другому випадку важливіше забезпечити високу ступінь подібності об’єктів усередині кожного кластера, а кластерів може бути скільки завгодно. В третьому випадку найбільший інтерес представляють окремі об’єкти, які не вписуються ні в один з кластерів[1].
Класифікувати алгоритми кластеризації в широкому сенсі можна на два наступних класи.
1. Ієрархічні і плоскі.
Ієрархічні алгоритми (також звані алгоритмами таксономії) будують не одне розбиття вибірки на непересічні кластери, а систему вкладених розбиттів. Таким чином, на виході ми отримуємо дерево кластерів, коренем якого є вся вибірка, а листям — найбільш дрібні кластера.
Так як основна вимога до системи це швидкодія, то розрахунок ієрархічними методами з вкладеними кластерами тільки ускладнить і сповільнить процес відображення просторових даних.
Плоскі алгоритми будують одне розбиття об’єктів на кластери.
Плоскі алгоритми вважаються досить швидкими та простими в дії, що повністю відповідає поставленим вимогам. До того ж одноразове розбиття дозволяє уникнути необхідності зберігати велику кількість проміжних даних.
2. Чіткі і нечіткі.
Чіткі (або непересічні) алгоритми кожному об’єкту вибірки ставлять у відповідність номер кластера, тобто кожен об’єкт належить тільки одному кластеру.
Так як основною ознакою об’єктів в кластерах є їх географічне положення, то чітка кластеризація найкращим чином вирішить проблему поділу об’єктів на чіткі групи.
Нечіткі (або пересічні) алгоритми кожному об’єкту ставлять у відповідність набір речових значень, що показують ступінь відносини об’єкта до кластерів. Тобто, кожен об’єкт відноситься до кожного кластеру з деякою вірогідністю.
При роботі з просторовими даними основною метою є наочність геоінформації, тому, якщо один і той же об’єкт буде входити в різні кластери, це значно ускладнить роботу і заплутає користувача.
Існують основні етапи розподілу об’єктів по кластерам. Для початку необхідно скласти вектор характеристик для кожного об’єкта — як правило, це набір числових значень. Однак існують також алгоритми, що працюють з якісними (категорійними) характеристиками.
В даному випадку вектор характеристик буде зберігати географічні координати просторових даних.
Після того, як ми визначили вектор характеристик, можна провести нормалізацію, щоб всі компоненти давали однаковий внесок при розрахунку "відстані". У процесі нормалізації всі значення приводяться до деякого діапазону, наприклад, [–1, –1] або [0, 1].
Для кожної пари об’єктів вимірюється "відстань" між ними — ступінь схожості. Існує безліч метрик, ось лише основні з них:
1. Евклідова відстань.
Найбільш поширена функція відстані. Являє собою геометричну відстань в багатовимірному просторі:
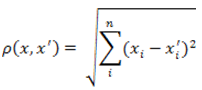
Рисунок 1 — Формула евклідової відстані
2. Квадрат евклідової відстані.
Застосовується для додання більшої ваги більш віддаленим один від одного об’єктів. Це відстань обчислюється таким чином:
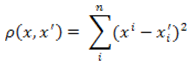
Рисунок 2 — Формула квадрата евклідової відстані
3. Відстань міських кварталів (манхеттенська відстань).
Ця відстань є середнім різниць по координатах. У більшості випадків, ця міра відстані приводить до таких же результатів, як і для звичайного відстані Евкліда. Однак, для цього заходу вплив окремих великих різниць (викидів) зменшується (так як вони не зводяться в квадрат). Формула для розрахунку манхеттенського відстані:
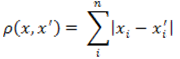
Рисунок 3 — Формула відстані міських кварталів
4. Відстань Чебишева.
Ця відстань може виявитися корисним, коли потрібно визначити два об’єкти як "різні", якщо вони різняться з якої–небудь однієї координаті. Відстань Чебишева обчислюється за формулою:
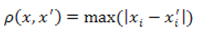
Рисунок 4 — Формула відстані Чебишева
Вибір метрики повністю лежить на досліднику, оскільки результати кластеризації можуть істотно відрізнятися при використанні різних заходів[8].
Для даного випадку найбільш підходяще "відстань" — Евклідова, так як дана міра ідеально підходить для розрахунку географічних відстаней. Решта "відстані" менш підходящі, так як вони вирішують специфічні завдання, які тільки ускладнять кластеризацію просторових даних.
Виходячи з вимог до системи і вибраних уподобань, можна визначитися з конкретним алгоритмом кластеризації.
Задачу кластеризації можна розглядати як побудову оптимального розбиття об’єктів на групи. При цьому оптимальність може бути визначена як вимога мінімізації середньоквадратичної помилки розбиття.
Алгоритми квадратичної помилки відносяться до типу плоских алгоритмів. Найпоширенішим алгоритмом цієї категорії є метод k–середніх. Цей алгоритм будує задане число кластерів, розташованих якнайдалі один від одного. Робота алгоритму ділиться на кілька етапів:

Рисунок 5 — Метод k–середніх
(анімація: обсяг — 20 КБ, кількість кадрів — 5, кількість циклів повторення — 6, розмір — 349x284)
Як критерій зупинки роботи алгоритму зазвичай вибирають мінімальну зміну середньоквадратичної помилки. Так само можливо зупиняти роботу алгоритму, якщо на кроці 2 не було об’єктів, що перемістилися з кластера в кластер.
До недоліків даного алгоритму можна віднести необхідність задавати кількість кластерів для розбиття, але в даному випадку це можна вважати позитивною властивістю даного методу.
Метод k–середніх також називають швидким кластерним аналізом, виходячи з назви, можна визначити, що даний метод найбільш відповідний для кластеризації просторових даних. Так обчислювальна складність методу k–середніх — O (nkl), де k — число кластерів, l — число ітерацій. Даний метод повністю відповідає поставленим вимогам: швидкодія, чіткість розподілу по кластерам. Також завдяки можливості спочатку ставити число кластерів можна розрахувати оптимальну кількість відображуваних об’єктів[2:3].
Так як основним завданням є скорочення кількості відображуваних просторових об’єктів без втрати даних, основною метою кластеризації є розуміння даних, шляхом виявлення кластерної структури. Так як вона має перевагу, яка полягає в тому, що число кластерів необхідно намагатися зробити менше.
Для ефективного вирішення даної проблеми необхідно реалізувати алгоритм, який відноситься до плоскої кластеризації, так як не буде необхідності у вкладених кластерах. Всю вибірку просторових даних необхідно один раз розбити на кластери.
Також алгоритм повинен ставитися до чіткої кластеризації, так як перетин кластерів неприпустимо. Один просторовий об’єкт буде ставитися тільки до одного кластеру.
Щоб визначити ступінь "схожості" просторових об’єктів на основі їх становища на карті, необхідно використовувати Евклідова відстань як міру відстані між об’єктами для об’єднання їх в кластери.
За даними порівняльного аналізу основних алгоритмів кластеризації можна зробити висновок, що найбільш підходящим алгоритм для розбиття на кластери просторових даних є алгоритм квадратичної помилки. А саме, метод k–середніх.
Даний метод найбільш ефективно мінімізує кількість відображуваних даних без втрати інформації. Недолік методу — необхідність вказувати кількість кластерів, ніяк не вплине на результати роботи.
Решта алгоритми тільки ускладнять роботу, збільшать час обробки даних і навантаження на трафік.
В цілому, можна сказати, що кластеризація — найбільш ефективне рішення проблеми відображення великої кількості просторових даних, так як даний метод дозволить компактно розподілити необхідну інформацію без втрати даних. Дане рішення великою мірою вплине на швидкість роботи геоінформаційної системи, а отже і зменшить витрати часу користувача.