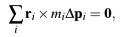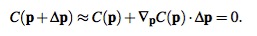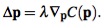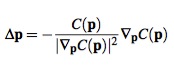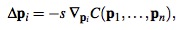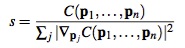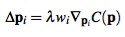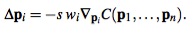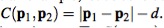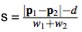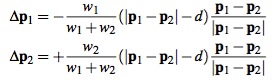Автор: Muller M., Heidelberger B., Hennix M., Ratcliff J.
Автор перевода: Радченко В.И., перевод 1, 2, 3 разделов статьи
Источник: Position Based Dynamics / Muller M., Heidelberger B., Hennix M., Ratcliff J. // Proceedings of Virtual Reality Interactions and Physical Simulations (VRIPhys), – Madrid, 2006, – pp 71-80, http://www.matthiasmueller.info ...
Самые популярные подходы при моделировании динамических систем в компьютерной графике базируются на силе. На основе накопленных внутренних и внешних сил, используя второй закон движения Ньютона, вычисляется ускорение. Определенный метод изменения времени используется, чтобы обновить скорости и положения объектов. Несколько методов моделирования (в основном твердых тел) используют динамику базирующуюся на импульсе, что позволяет непосредственно управлять скоростями. В этой статье представлен подход, который не оперирует понятием скорость, а работает непосредственно с позициями. Главное преимущество этого подхода – его контролируемость. С его помощью можно избежать проблем возникающих в системах основанных непосредственно на силах. Кроме того, могут быть легко обработаны и полностью решены ограничения и столкновения, проецируя точки к допустимым местоположениям. Авторы статьи использовали этот подход при создании симулятора ткани реального времени, который является частью физической библиотеки для игр. Эта статья демонстрирует возможности и выгоды метода.
Исследование в области анимирования основанного на физике в компьютерной графике сосредоточены на обнаружении новых методов моделирования физических явлений, таких как динамика твердых тел, деформируемых объектов или потока жидкости. В отличие от вычислительных наук, где главное внимание сосредоточено на точности, главные задачи здесь – стабильность, надежность и скорость, в то время как результаты должны оставаться визуально правдоподобными. Поэтому, существующие методы вычислительных наук не могут быть использованы в том виде в котором они есть. Фактически, главное оправдание проведения исследований в области физического моделирования в компьютерной графике состоит в том, что можно придумать специализированные методы обусловленные особыми потребностям предметной области. Методика, которая представлена в этой статье, попадает в эту категорию.
Традиционный подход к моделированию динамических объектов работает с силами. В начале каждого временного шага пересчитываются внутренние и внешние силы. Примеры внутренних сил – упругие силы в деформируемых объектах или силы вязкости и давления в жидкостях. Сила тяжести и силы столкновения – примеры внешних сил. Второй закон Ньютона движения связывает силы с ускорением тела и его массой. Используя плотность или усредненные массы вершин, силы преобразуются в ускорение. Любая схема интегрирования времени может быть использована, чтобы сначала вычислить скорости на основе ускорений и затем положения на основе скоростей. Некоторые подходы для управления анимацией используют импульсы вместо сил. Поскольку импульсы непосредственно изменяют скорости, один уровень просчетов может быть пропущен.
В компьютерной графике и особенно в компьютерных играх часто желательно иметь прямое управление положениями объектов или вершинами полигональной сетки. Пользователь может привязать вершину к кинематическому объекту или удостовериться, что вершина всегда остается вне определенной области. Метод предлагаемый здесь работает непосредственно с позициями, что делает такие манипуляции легко реализуемыми.
Кроме того, используя данный подход, возможно непосредственно управлять изменением положения объекта, таким образом, избегая промахов(просчетов) по сравнению с прямыми физическими расчетами. Таким образом, главные особенности и преимущества динамики основанной на позициях:
Следующий источник [13] дает хороший краткий обзор методов, используемых в компьютерной графике для симуляции деформируемых объектов, например, массово-пружинные системы, методы конечных элементов или подходы конечной разности. Динамика основанная на позициях упоминается в ряде источников, без явного описания и определения полной структуры.
Jakobsen [11] построил свой движок Fysix на основе этого подхода. Его основная идея состояла в том, чтобы использовать интегрирование Верле и управлять положениями непосредственно. Поскольку скорости неявно сохранены текущими и предыдущими положениями, следовательно они обновляются при пересчете позиций. В своей работе он сосредоточился, главным образом, на ограничениях расстояния, и только дал неопределенные намеки на то, как могли быть обработаны более общие ограничения.
В этой статье представлен полностью общий подход, который обрабатывает обобщенные ограничения. В ней также сосредотачивается внимание на важной проблеме сохранения импульса при проецировании позиций. Скорости обрабатываются непосредственно вместо того, чтобы хранить предыдущие положения, что делает моделирование торможения и трения намного легче.
Desbrun [6] и Provot [14] используют проекционные ограничения в массово-пружинных системах, чтобы предотвратить пружины от чрезмерного растяжения. В отличие от динамики основанной на позициях, проекции используются только в качестве процесса полировки тех пружин, которые растянуты чрезмерно, а не как основной метод моделирования.
Bridson и др. использует традиционный подход основанный на силах для моделирование ткани [1] и совмещают его с геометрическим алгоритмом решения столкновений, чтобы удостовериться, что импульсы решения столкновения остаются в рамках допустимых границ. Такой же подход используется для кинематической коррекции столкновений, предложенной Volino и др. [18] .
Muller и др. [12] моделирует деформируемые объекты, перемещая точки к целевым положениям цели, которые соответствуют остальным ограничениям текущего состояния объекта. Их метод интегрирования является самым близким к тому, который предлагается в этой статье.
Fedor [8] использует подход Jakobsen, чтобы моделировать модели людей в играх. Его метод специализируется на проблеме моделирования человеческих моделей. Он использует несколько скелетных представлений и поддерживает синхронизацию между ними, проецирую существующие ограничения.
Faure [7] использует схему интегрирования Верле, модифицируя позиции, а не скорости.
Мы определяем общие ограничения через функцию ограничения как [3] и [17] . Вместо того, чтобы вычислить силы как производную энергии функции ограничения, мы непосредственно вычисляем состояние равновесия и проецируем позиции. Результаты рассматриваемого метода подобны результатам предложенным в [9] и [2] , но получены в результате применения динамики, основанной на позициях.
В этой секции будут сформулированны общие положение рассматриваемого подхода. В статье предполагается трехмерное пространство. Однако, подход работает одинаково хорошо и для двухмерного.
Мы представляем динамический объект множеством из N вершин и M ограничений. Каждая i-ая [1..N] вершина имеет массу mi, позицию xi и скорость vi. Каждое j-ое [1..M] ограничение состоит из:
Ограничение j с типом «равенство» удовлетворено если CJ (xi1..., xinj) = 0. Если его тип – «неравенство» тогда, оно удовлетворено если CJ (xi1..., xinj) ≥ 0. Параметр жесткости kj определяет силу ограничения в диапазоне от нуля до единицы.
На основе этих данных и временного шага Δt, динамический объект моделируется следующим образом:
Сроки (1) - (3) просто инициализируют начальное состояние. Основная идея алгоритма описана в строках (7), (9) - (11) и (13) - (14). В строке (7), используя метод Эйлера, вычисляется предварительные позиции для новых местоположений вершин. В строках (9) - (11) происходит итеративное корректирование полученных позиций, таким образом чтобы они удовлетворяли ограничениям. В строках (13) и (14) обновляются текущие положения вершин и значения скоростей. Этот этап соответствует шагу интегрирования Верле и модификации текущего положения [Jak01]. Однако, работа со скоростями в явном виде предоставляет более интуитивный способ контролировать их.
Скоростями управляют в строках (5), (6) и (16). Строка (5) позволяет учитывать внешние силы к системе. В данном случае в систему добавлена сила тяжести, поэтому строка имеет вид vi ← vi + Δt * g, где g – ускорение свободного падения. В строке (6), если это необходимо, могут быть затушены скорости. Наконец, в строке (16), скорости вершин изменяются согласно коэффициентам трения и восстановления.
Ограничения C1..., CM решаются в процессе моделирования. В дополнение к этим ограничениям в строке (8) производится генерирование ограничений столкновения Мcol, которые изменяются на каждом временном шаге. Шаг проецирования в строке (10) рассматривает как фиксированные ограничения так и ограничения столкновения.
Устойчивость метода объясняется тем, что шаги интегрирования (13) и (14) не экстраполируют вслепую, как это делают традиционные методы, а перемещают вершины в физически корректное положение, учитывающее наложенные ограничения. Единственный возможный источник для неустойчивости является вычислитель ограничений, который использует метод Ньютона-Рафсона. Его стабильность не зависит от размера временного шага, но зависит от формы функций ограничения.
Рассмотренный метод интегрирования не попадает в категорию неявных или явных схем. Если производить только один пересчет ограничений за временной шаг, оно больше походит на явную схему. Увеличивая число повторений, возможно добиться заданной жесткости, и алгоритм будет вести себя больше как неявная схема.
Входными данными этапа вычисления ограничений являются M фиксированных ограничений, дополнительные ограничения столкновения Мcol и предполагаемые положения p1..., pN для новых местоположений вершин. Алгоритм пытается изменить предполагаемые позиции, таким образом, чтобы они удовлетворяли всем ограничения. Получающаяся система уравнений нелинейна, так как даже простое ограничение расстояния C (p1, p2) = |p1 - p2 | - d приводит к нелинейному уравнению. Чтобы решить набор уравнений и неравенств, используется расширение итеративного метода Гаусса — Зейделя. Оригинальный метод Гаусса — Зейделя может обращаться только с линейной системой. Часть, которая заимствуется из этого метода, является идеей решить каждое ограничение одно за другим. Однако, в отличие от метода Гаусса — Зейделя, решение ограничения является не линейной операцией. Каждое из ограничений вычисляется повторно и позиции проецируются в допустимые местоположения, с точки зрения только данного ограничения. Этот метод значительно ускоряет процесс сходимости, потому изменения позиций учитываются уже на текущей итерации. Результат итерации зависит от порядка, в котором были решены ограничения. В системах с большим количеством ограничений процесс может привести к колебаниям, если порядок вычисления ограничений изменяется
Выполнить проецирование множества точек в согласно определенному ограничению, предполагает перемещение позиции точек таким образом, чтобы это расположение удовлетворяло ограничение. При выполнении данной операции наиболее важным является сохранение значения импульса и кинетического момента. Пусть, Δpi – смещение i-ой вершины. Импульс сохраняется при выполнении следующего условия:
что говорит о том что геометрический центр масс остался неизменным.
Кинетический момент сохраняется при выполнении следующего условия:
Если проецирование нарушает одно из этих условий, это приводит к возникновению так называемых «призрачных сил», которые действуют как внешние силы, перемещающие и вращающие объект. Сохранять импульсы должны только внутренние ограничения. Столкновения или другие внешние воздействия имеют глобальный эффект на объект.
Метод проецирования ограничений, предлагаемый авторами, созраняет как импульс, так и кинетический момент. Рассмотрим ограничение включающее n точек p1 , . . . , pn, функцию ограничения C и коэффициент жесткости k. Для внутренних ограничений функция C инваринтна при вращении или перемещении объекта. Это означает, что поворот или перемещение точек не изменяте значения функции ограничения. Градиент ∇pC совпадает с направлением максимального изменения расчитываемого ограничения. Если для набора точек выбрать, соответсвующие значению градиента, корректирующие величины, то импульс и кинетический моиент системы будут сохранены. Для имеющихся точек p необходимо найти корректирующие Δp, такие что C(p + Δp) = 0. Это уравнение может быть представленно в виде:
Подобрать Δp таким образом чтобы он соответсвовал ∇pC, означает найти скаляр λ, такой что
Конечная формула для Δp имеет вид
который является стандартным шагом для итеративного метода Ньютона-Рафсон решения нелинейного уравнения, имеющего единственное ограничение. Для коррекции каждой отдельно взятой точки имеем
где масштабирующий коэффициент одинаков для всех точек и выражается как
Если точки имеют различные массы, то уравнение для вычисления коррекции позиции точки примет вид
а значение масштабирующего коэффициента будет вычисляться как
Конечная формула учитывающая массы точек имеет вид
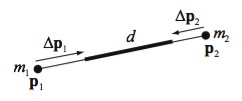
В качестве примера, рассмотрим ограничения на расстояние
Частные производные будут иметь вид
Коэффициент масштабирования
Окончательные формулы коррекции точек тмеют вид
Графическая интерпретация рассмотренного примера приведена ниже.
До сих пор не рассматривался тип и жесткость k ограничения. Если тип ограничения “равенство”, то проецирование выполняется всегда. Если тип – “неравенство”, проецирование производится, только если C (p1, ..., р) < 0.
Есть несколько способов использования параметра жесткости. Самый простой вариант домножить поправки Δp на коэффициент жескости k. Тем не менее, для нескольких итераций коррекции, воздействие k становиться нелинейным.
В статье был представлен подход, использующий динамику основанную на позициях, который поддерживает общие ограничения, сформулированные через функции ограничения. Используя этот подход положениями возможно управлять непосредственно во время моделирования, на много упрощает обработку столкновений и ограничений, и делает возможным непосредственный контроль анимируемой сцены.
Авторы реализовали симулятор ткани на основе рассмотренного подхода, который обладает такими особенности как: обработка взаимодействия ткани с твердыми телами, ткани с самой собой, привязка частей ткани к динамическим твердым телам. Результаты приведены ниже.
Тема, которую не рассматривается в этой статье, является симуляция твердых тел. Однако, подход, который здесь представлен, может быть легко расширенным для работы с твердыми объектами. Вместо вычисления ряда линейных и угловых импульсов для обработки столкновений как это часто делают, движение и вращение могут быть установлены телу в точках столкновения, а линейные и угловые скорости должны будут установлены соответственно после того, как будут вычислены все ограничения.
1. BRIDSON R., FEDKIW R., ANDERSON J.: Robust treatment of collisions, contact and friction for cloth animation. Proceedings of ACM Siggraph (2002), 594–603.
2. BRIDSON R., MARINO S., FEDKIW R.: Simulation of clothing with folds and wrinkles. In ACM SIGGRAPH Symposium on Computer Animation (2003), pp. 28–36.
3. BARAFF D., WITKIN A.: Large steps in cloth simulation. Proceedings of ACM Siggraph (1998), 43–54.
4. BARAFF D., WITKIN A., KASS M.: Untangling cloth. In Proceedings of the ACM SIGGRAPH (2003), pp. 862–870.
5. CLAVET S., BEAUDOIN P., POULIN P.: Particle-based viscoelastic fluid simulation. Proceedings of the ACM SIGGRAPH Symposium on Computer Animation (2005), 219–228.
6. DESBRUN M., SCHREDER P., BARR A.: Interactive animation of structured deformable objects. In Proceedings of Graphics Interface ’99 (1999), pp. 1–8.
7. FAURE F.: Interactive solid animation using linearized displacement constraints. In Eurographics Workshop on Computer Animation and Simulation (EGCAS) (1998), pp. 61–72.
8. FEDOR M.: Fast character animation using particle dynamics. Proceedings of International Conference on Graphics, Vision and Image Processing, GVIP05 (2005).
9. GRINSPUN E., HIRANI A., DESBRUN M., SCHRODER P.: Discrete shells. In Proceedings of the ACM SIGGRAPH Symposium on Computer Animation (2003).
10. IRVING G., TERAN J., FEDKIW R.: Invertible finite elements for robust simulation of large deformation. In Proceedings of the ACM SIGGRAPH Symposium on Computer Animation (2004), pp. 131–140.
11. JAKOBSEN T.: Advanced character physics U the fysix-engine. www.gamasutra.com (2001).
12. MULLER M., HEIDELBERGER B., TESCHER M., GROSS M.: Meshless deformations based on shape matching. Proceedings of ACM Siggraph (2005), 471–478.
13. NEALEN A., MULLER M., KEISER R., BOXERMAN E., CARLSON M.: Physically based deformable models in computer graphics. Eurographics 2005 state of the art report (2005).
14. PROVOT X.: Deformation constraints in a mass-spring model to describe rigid cloth behavior. Proceedings of Graphics Interface(1995),147–154.
15. RATCLIFF J.: Rocket - a viewer for real-time phyics simulations. www.physicstools.org (2004).
16. TESCHNER M., HEIDELBERGER B., MULLER M., POMERANERTS D., GROSS M.: Optimized spatial hashing for collision detection of deformable objects. Proc. Vision, Model- ing, Visualization VMV 2003 (2003), 47–54.
17. TESCHNER M., HEIDELBERGER B., MULLER M., GROSS M.: A versatile and robust model for geometrically complex deformable solids. Proceedings of Computer Graphics In- ternational (CGI) (2004), 312–319.
18. VOLINO P., COURCHESNE M., MAGNENAT- THALMANN N.: Versatile and efficient techniques for simulating cloth and other deformable objects. Proceedings of ACM Siggraph (1995), 137–144.