Автор: Карабчевский В.В., Радченко В.И.
Источник: Тезисы докладов XXI Международной студенческой научно-технической конференции Графика XXI века
– Севастополь, 2010 – С.76-78.
Линии и поверхности занимают важное место в компьютерной графике и начертательной геометрии. С их помощью создаются наглядные модели многих процессов и прослеживается их течение во времени. Они играют важную роль в конструировании и производ¬стве. Очевидными примерами этого являются разработка и производство авто¬мобильных кузовов, корабельных корпусов, авиационных фюзеляжей и крыльев; пропеллеров, турбин, компрессоров и лопастей вентиляторов; посуды, мебели и других предметов. В этом случае сущность конструирования либо по функциональным, либо по эстетическим причинам составляет форма или геометрия поверхности. Линии и поверхности также используются для представления данных, полученных в медицине, геологии, физике и других естественных науках.
Простейшими способами получения трехмерной поверхности являются вращение двумерного объекта, например прямой или плоской кривой вокруг оси в пространстве, или перемещение объекта, например отрезка, ломанной или кривой вдоль некоторой линии в пространстве. Такие поверхности называются поверхностями вращения и заметающими поверхностями соответственно. Обычные квадратичные поверхности, такие как сфера, конус, цилиндр, эллипсоид, параболоид вращения и гиперболоид вращения являются также и поверхностями вращения.
Существует много поверхностей, для которых невозможно или достаточно трудоемко получить аналитическое описание. Эти поверхности пред¬ставляются в кусочном виде. В рассуждениях используется векторное параметрическое представление, потому что оно не зави¬сит от осей, устраняет бесконечные значения углов наклона относительно некото¬рой произвольной системы координат, устраняет неоднозначность представления многозначных поверхностей и пространственных функций, облегчает представление поверхностей в однородных координатах, и такое представление совместимо с использованием преобразований трехмерных однородных координат.
Существуют две основные идеи, лежащие в основе методов описания подобных поверх¬ностей. В первой математическую модель стараются создать по заранее известным данным. Во второй кривую или поверхность стараются создать с самого начала. В этом случае кроме количественных критериев требуется учет практического опыта, и часто необходимо интерактивное вмешательство разработчика. В первое время отрасли, связанные с числовыми па¬раметрами, например, конструирование, тяготели к первому подходу, тогда как отрасли, учитывающие визуальные, осязательные или эстетические факторы, например дизайнеры и художники, использовали второй.
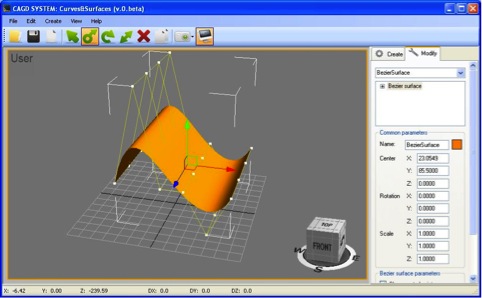
В ходе исследования рассматриваемой предметной области были изучены способы представления, методы расчета и визуализации пространственных кривых и поверхностей различного вида. Рассмотренные алгоритмы легли в основу программной реализации интерактивной системы моделирования. Разработанный трехмерный графический редактор позволяет работать с такими видами пространственных кривых как кубические сплайны, кривые Безье, В-сплайны. В нем реализованы следующие способы представления поверхностей: поверхности Кунса, поверхности Безье, В-сплайн поверхности.
Рисунок 1 — Интерфейс разработанной интерактивной системы моделирования
Приложение обеспечивает возможность создания и редактирования кривых и поверхностей, изменения параметров любого объекта, а также его масштабирование, перенос, поворот и удаление. Система обладает интуитивно понятным пользовательским интерфейсом: программный продукт обеспечивает пользователю максимально понятную и простую работу за счет продуманного оформления интерфейса, контекстных подсказок, горячих клавиш и предупреждений. За основу был взят стандартный интерфейс, существующих профессиональных систем моделирования, таких как: 3ds Max, Maya, Blender.
Структура программной системы спланирована таким образом, что расширение системы, посредством добавления новых программных модулей или внесения изменений в существующие, не представляет собой особых сложностей и не повлечет за собой необходимости повторного проектирования и изменения всей системы в целом. В перспективе предполагается расширение функциональности приложения, добавление поддержки работы с NURBS кривыми и поверхностями.
1. Роджерс Д., Адамс Дж. «Математические основы машинной графики» – М.:Мир, 2001. – 606 с.
2. Шикин Е.В., Плис Л.И. «Кривые и поверхности на экране компьютера. Руководство сплайнам для пользователей» – М.:ДИАЛОГ-МИФИ, 1996. – 240с.
3. Farin G. «Curves and surfaces for CAGD. A practical guide» – Morgan-Kaufmann, 2002. – 499 p.