Применение технологии NURBS для создания трехмерных компьютерных моделей

Аннотация

У статті розглядаються методи та алгоритми представлення просторових кривих і поверхонь в комп'ютерній графіці засобами NURBS. Цілі роботи - отримання поглиблених знань і практичних навичок в досліджуваній області графічного моделювання; програмна реалізація алгоритмів роботи з NURBS; створення власної функціональної бібліотеки на основі реалізованих алгоритмів.

Введение

NURBS, Неоднородные Рациональные B-сплайны, являются математическим представлением 3-D геометрии, которое может точно описать любую форму от простой 2-D линии, круга, дуги или кривой до самой сложной 3-D органической поверхности. В силу своей гибкости и точности, модели NURBS могут использоваться в различных областях, от иллюстрации и анимации до проектирования в производстве [1].

NURBS широко применяются для задания кривых и поверхностей во многих современных CAD системах. С помощью В-сплайнов можно представить достаточно сложные поверхности, что позволяет построить гибкую систему моделирования. Примерами систем, поддерживающих работу с В-сплайнами, являются Rhinoceros, T-Flex, Unigraphics и др.

В статье рассматривается применение технологии NURBS на примере разработки собственной программной библиотеки для работы с NURBS и построения на ее основе системы трехмерного моделирования.

Постановка задачи

Существующие профессиональные среды моделирования предоставляют обширную функциональность и поддержку своим клиентам, но по своей природе являются закрытым коммерческим программным обеспечением. В силу этого невозможно использовать, модифицировать их исходный код или узнать подробности реализации программной архитектуры этих систем. Целью работы является проектирование собственной модификации интерактивной графической системы, позволяющей создавать и редактировать пространственные кривые и поверхности различного вида. Составные элементы данной системы могут быть в дальнейшем использованы в учебном процессе при решении прикладных задач компьютерной графики и моделирования.

Материал исследования

Алгоритмы представления и расчета NURBS легли в основу программной реализации функциональной библиотеки для работы с кривыми и поверхностями. Кроме NURBS, в разработанной библиотеке реализованы методы работы со следующими видами пространственных кривых и поверхностей: кубические сплайны, поверхности Кунса [2], а также В-сплайны, кривые и поверхности Безье, представляющие собой частный случай NURBS [1]. Весь комплекс базовых примитивов предоставляет широкие возможности и перспективы для дальнейшего расширения функциональности библиотеки и ее практического применения.

На базе этой библиотеки была разработана интерактивная система моделирования, которая обеспечивает возможность создания и редактирования кривых и поверхностей, изменения их параметров, применение стандартных преобразований (перенос, масштабирование, поворот). Изменение опорных точек и параметров объектов происходит в интерактивном режиме с немедленной визуализацией результатов расчетов на экране.

Система обладает интуитивно понятным пользовательским интерфейсом: программный продукт обеспечивает пользователю максимально понятную и простую работу за счет продуманного оформления интерфейса, контекстных подсказок, горячих клавиш и предупреждений. За основу был взят стандартный интерфейс, существующих профессиональных сред моделирования

Разработанная система, написана на языке Visual С++ в интегрированной среде разработки Microsoft Visual C++ 2008 с использованием компонентов программной технологии .NET Framework 3.5 и графической библиотеки OpenGL. Выбор программных средств, для разработки проекта был сделан исходя из специфики поставленной задачи. Некоторые из особенностей которой:
- наличие удобного визуального интерфейса, схожего с большинством существующих профессиональных систем моделирования;
- наличие сложной иерархии классов и необходимость объектно-ориентированного подхода к представлению предметной области, позволяющего разрабатывать большие программные комплексы быстрее, используя повторно имеющие модули, обеспечивать инкапсуляцию данных, полиморфизм операций, наследование свойств и методов.

Система позволяет работать как с базовыми NURBS, так и с комплексными геометрическими моделями образованными на их основе. На рисунке 1 приведен пример линейчатой поверхности, у которой в качестве направляющих используются две NURBS кривые.

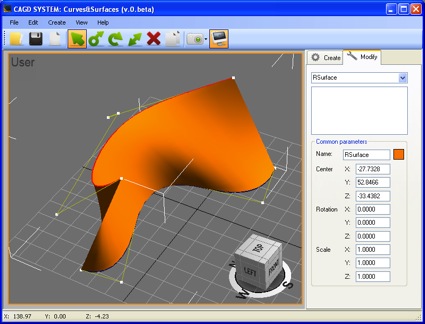
Рисунок 1 — Линейчатая поверхность на основе двух NURBS-кривых

Так же возможности разработанной библиотеки нашли практическое применение при решении задач генерации, визуализации и анализа поверхности ландшафта (рис. 2), расчета линий равного уровня, восстановления трехмерной геометрии объекта на основе существующих двумерных графических файлов.

Приложения, использующие разработанную программную библиотеку, получили высокие отзывы и оценки на Международной студенческой научно-технической конференции «Графика XXI века» в Севастополе, прошедшей 4-8 октября 2010 года [3], а также на международной студенческой олимпиаде 2010-2011 учебного года с систем автоматизированного проектирования и компьютерного моделирования в машиностроении, проведенной на базе Хмельницкого национального университета.

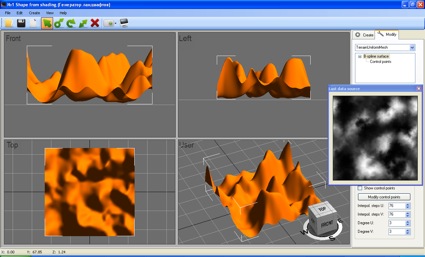
Рисунок 2 — Ландшафт, представленный В-сплайн поверхностью на основе карты высот

Выводы и перспективы

На основе исследования предметной области была разработана система моделирования, позволяющая работать с различными видами кривых и поверхностей (в частности, В-сплайны и NURBS). Разработанный графический редактор может быть в дальнейшем использован в образовательных целях на курсе «Графическое и геометрическое моделирование и интерактивные системы» в качестве демонстрации примера моделирования трехмерных объектов. В перспективе предполагается расширение функциональности приложения и оптимизация алгоритмов расчета геометрии.

Список использованной литературы

1 Piegl L., Tiller W., «The NURBS Book. 2nd Edition» – Springer, 1997. – 646 p.
2 Роджерс Д., Адамс Дж., «Математические основы машинной графики» – М.:Мир, 2001. – 606 с.
3 Карабчевский В.В., Радченко В.И., «Исследование методов и алгоритмов представления пространственных кривых и поверхностей в компьютерной графике» // «Графика XXI века. Тезисы докладов XXI Международной студенческой научно-технической конференции» – Севастополь, 2010 – С.76-78.