K. Khoshelham - Точный анализ данных датчика глубины контроллера Kinect

Ключевые слова: Точность, ошибки, диапазон изображения, выбор камеры, RGB-D, лазерного сканирования, облако точек, калибровки, врутреннее отображение.

Аннотация:

Эта статья представляет собой исследование геометрического качества глубина данных, полученных датчиком Kinect. На основе математической модели измерения глубины с помощью датчика представлен теоретический анализ ошибок, который дает представление о факторах, влияющих на точность данных. Экспериментальные результаты показывают, что случайная погрешность измерения глубины увеличивается с увеличением расстояния до датчика, и колеблется от нескольких миллиметров до около 4 см при максимальной дальности датчика. Достоверность данных, также находится под влиянием низкого разрешения измерения глубины.

1. Введение

Низкая стоимость устройств сканирования является привлекательной альтернативой для дорогих лазерных сканеров в областях применения, таких как внутреннее отображение, наблюдения, робототехника и судебно-медицинской экспертиза. Недавним решением является датчик Microsoft Kinect (Microsoft, 2010). Kinect в первую очередь предназначен для естественного взаимодействия в среде компьютерных игр (PrimeSense, 2010). Тем не менее, характеристики данных, захваченных Kinect привлекли внимание исследователей из области отображения и 3D моделирования. Последние демонстрации возможностей Kinect для 3D моделирования помещениях можно увидеть в работе Генри и соавт. (2010).

Kinect датчик фиксирует глубину и цвет изображения одновременно с частотой 30 кадров в секунду. Интеграции и глубины цвета данных результатов в цвете для каждой точки, которая содержит около 300000 точек в каждом кадре. При регистрации последовательных изображений глубине можно получить повышенную плотность точки, но и создать полную карут помещения, возможно, в режиме реального времени.Коррекция систематических ошибок является необходимым условием для выравнивания глубины и цветовые данные, как и полагается по идентификации математической модели измерения глубины и параметры калибровки участие. Характеристика случайных ошибок является важным и полезным в дальнейшей обработке данных о глубине, например, взвешивание точки пар в регистрации алгоритм (Rusinkiewicz и Levoy, 2001).

Так как Kinect является недавней разработкой - она была выпущена в ноябре 2010 года - существует мало информации о геометрическом качестве его данных. Геометрические исследования и калибровки подобных датчиков диапазона, такие как SwissRanger, была темой нескольких предыдущих работах (Брейер и др., 2007;. Kahlmann и Ingensand, 2008; Kahlmann и др., 2006;. Lichti, 2008). Тем не менее, принцип измерения глубины в Kinect отличается от SwissRanger.

В этой статье мы концентрируемся на глубине данных. Цель этого документа заключается в обеспечении понимания геометрического качества Kinect данных о глубинах, на основе анализа точности и плотности точек. Мы представляем собой математическую модель для получения 3D-координаты объекта из сырых измерений изображений, и обсудим калибровку параметров, входящих в модель. Кроме того, теоретические модели случайных ошибок проверены экспериментами.

Работа продолжается описанием принципа измерения глубины, математическими моделями и параметрами калибровки в разделе 2. В разделе 3 обсуждаются источникы ошибок??. В разделе 4 модели проверяется с помощью ряда экспериментов и приводятся результаты. В статье приводятся некоторые замечания в разделе 5.

2. Принцип измерения глубины методом триангуляции

Сенсор Kinect состоит из инфракрасного излучателя, инфракрасной камеры и камеры RGB. Изобретатели описали измерение глубины, как процесс триангуляции (Фридман и др.., 2010). Лазерный источник испускает один луч, который разделен на несколько пучков с дифракционной решеткой для создания постоянной структуры и проецируется на сцену. Эта модель захватывается инфракрасной камерой и соотносится с эталонной. Эталонная модель получается путем захвата плоскости на известном расстоянии от датчика, и хранится в памяти датчика. Когда спектр проецируется на объект, расстояние до сенсора меньше или больше, чем в контрольной плоскости положение спектра в инфракрасном изображении будет смещено в сторону базовой между лазерным проектором и перспективы центра инфракрасной камеры. Эти изменения измеряются для всех пятен простой процедурой корреляции изображения, что дает несоответствие изображения. Для каждого пикселя расстояние до датчика может быть получен из соответствующего неравенства, как описано в следующем разделе. Рисунок 1 иллюстрирует измерения глубины от спектр-картины.

Рисунок 1. Слева: инфракрасное изображение картины крапинками проецируется на объект; Справа: получившееся изображение глубины.

2.1 Математическая модель

На рисунке 2 показано соотношение между расстоянием от точки к объекту с датчика по отношению к плоскости отсчета и измеряется неравенство г. Чтобы выразить 3d координат точек объекта, мы рассматриваем глубину системе координат с началом в перспективе центр инфракрасной камеры. Ось Z ортогональна плоскости изображения по отношению к объекту, перпендикулярной оси Х по оси Z в направлении базовой б между инфракрасным центре камеры и лазерного проектора, а ось Y ортогональна X и Z образует правстороннюю систему координат.

Предположим, что объект находится на опорной плоскости на расстоянии Zo к датчику, и пятно на объект захвачено на плоскости изображения инфракрасной камеры. Если объект перемещается ближе (или дальше от) датчик расположения пятна на плоскости изображения будут смещен в направлении х. Он измеряется в пространстве изображения, как несоответствие г, соответствующего точке А в пространстве объектов. Из подобия треугольников имеем:

и:

где Zk обозначает расстояние (глубина) в точке к в пространстве объекта, б является базовой длине, F-фокусное расстояние инфракрасной камерой, D является смещение точки А в пространстве объектов, и г является наблюдаемое несоответствие в пространстве изображения. Подставляя D из (2) в (1) и выражая Zk с точки зрения другой получим:

Уравнение (3) является основной математической модели для вывода глубины от наблюдаемого неравенства при условии, что постоянные параметры Zo, F и B могут быть определены по калибровке. Z координаты точки вместе с е определяет масштаб изображения в этой точке. Контурный объект координаты каждой точки может быть вычислена из его координат изображения и масштаба:

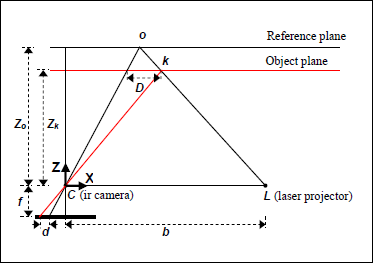
Рисунок 2. Схематическое изображение глубины несоответствие отношения.

где хк и ук образ координаты точки, хо, уо-координаты главной точки, а х и у корректировки искажений объектива, для которого различные модели с различными коэффициентами существует; см., например, (Fraser, 1997). Заметим, что здесь мы предполагаем, что образ системы координат идет параллельно с базовой линией и, следовательно, находится в системе координат глубины.

2.2 Калибровка

Как упоминалось выше, калибровка параметров, входящих в математическую модель для расчета 3D-координаты из сырых измерений изображений включают в себя:

фокусное расстояние (F);
основное смещение точки (хо, Уо);
коэффициенты искажения объектива (х, у?);
длина базы (б);
эталонное расстояние (Zo).

Кроме того, можно считать смещение угла между осью х системы координат изображения и базовой линии. Однако это не влияет на расчет координат объекта, если мы определим системы координат глубины параллельными с изображением системы координат вместо базовой линии. Мы можем, таким образом, игнорировать это смещение угла.

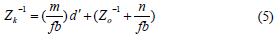
Уравнение (5) выражает линейную зависимость между глубиной обратной точки и соответствующие нормированные неравенства. Наблюдая нормированного несоответствие по ряду точек объекта (или плоскости) при известном расстоянии к датчику коэффициенты этой линейной зависимости можно оценить методом наименьших квадратов моды. Тем не менее, включение нормализации параметров не позволяет определить и б Zo отдельно.

2.3 Интеграция глубины и цвета

Интеграция глубины и цвета данных требует ориентации камеры RGB относительно глубины системе координат. Так как мы определили систему координат в глубине перспективы в центре инфракрасной камеры мы можем выполнить ориентации стерео калибровка двумя камерами. Параметры, подлежащие оценке включает в себя три вращения между системой координат камеры в камеру RGB и ИК-камеры и 3-й позиции из перспективных центре камеры RGB в системе координат, ИК-камеры. Кроме того, внутренние параметры ориентации камеры RGB, то есть фокусное расстояние основного смещения точки и параметры дисторсии объектива должна быть оценены. Как только эти параметры известны, мы можем спроектировать каждые 3 точки из облака точек на изображение RGB.

3. Точность глубины и плотность точек

Точность и плотность точек две важные меры по оценке качества облаков точек. В следующих разделах факторы, влияющие на точность и плотность Kinect данные обсуждались и теоретические модели случайных ошибках представлен.

3.1 Источники ошибок

Ошибки и несовершенства Kinect данных могут происходить из трех основных источников:
- датчик;
- установки измерений ;
- свойства поверхности объекта производителя
Недостаточная калибровка и / или ошибки в оценке параметров калибровки могут привести к систематической ошибке в объекте, координаты отдельных точек. Такие систематические ошибки могут быть устранены путем правильной калибровке, как описано в предыдущем разделе. Неточность измерения неравенства в алгоритм корреляции и ошибки округления при нормализации привести к ошибкам, которые, скорее всего, случайный характер.

Ошибки, возникающие при измерении установки в основном связаны с условиями освещения и визуализации геометрии. Условия освещения влияют на соотношение и измерение неравенства. В ярком свете лазерных пятен появляется в низкой контрастности в инфракрасном изображении, которое может привести к выбросам или разрыв в результате облако точек.Геометрию изображения включает в себя расстояние до объекта и ориентации объекта по отношению к поверхности датчика.Рабочий диапазон датчика составляет от 0,5 м до 5,0 м в соответствии со спецификациями и, как мы увидим в следующем разделе, случайная погрешность измерения глубины увеличивается с увеличением расстояния до датчика. Кроме того, в зависимости от изображения геометрии, часть сцены может быть закрыта или находится в тени. На рисунке 1, в правой части окна закрыта, так как не видно на инфракрасную камеру. В левой части окна тень, потому что она не освещается лазером, но фиксируются в инфракрасном изображении. Тени выглядят как пробелы в облаке точек.

Свойства поверхности объекта также влияют на измерения точек. Как видно на рисунке 1, гладкими и блестящими поверхностями, которые кажутся переэкспонированных в инфракрасном изображении (в нижней части окна) препятствуют измерения неравенства, и в результате получается разрыв в облаке точек.

3.2 Теоретическая модель случайных ошибкок

Предполагая, что в уравнении (5) калибровки параметры определяются точно и, что D 'является случайной величиной с нормальным распределением мы можем распространять дисперсии несоответствие измерений для получения дисперсии измерения глубины следующим образом:

После упрощения это приводит к следующему выражению для стандартного отклонения глубины:

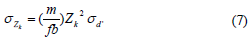
Вместе с d и Zk соответственно, стандартное отклонение измеренной нормированной неравенства и стандартное отклонение расчетной глубины. Уравнение 7 в основном выражает то, что случайная ошибка измерения глубины пропорционально квадрату расстояния от датчика до объекта. Так как глубина, участвующих в расчете контурной координат, см. формулу 4, можно ожидать, что ошибка в X и Y, что и вторая функция порядка глубины.

3.3 Плотность точек

Разрешение инфракрасной камеры, то есть размер пиксела, определяет точку интервал глубины данные на плоскости XY (перпендикулярно оси камеры). Поскольку каждый образ содержит глубину постоянной 640х480 точек плотность точек будет уменьшаться с увеличением расстояния от поверхности объекта от датчика. Учитывая плотность точек, как количество точек на единицу площади, в то время как количество точек остается постоянным площадь пропорциональна квадрату расстояния от датчика. Таким образом, плотность точек обратно пропорциональна квадрату расстояния от датчиков, а именно:

Глубина резкости определяется по количеству бит на пиксел используется для хранения несоответствие измерений.Kinect измерения неравенства хранятся как 11-разрядных целых чисел, где 1 бит зарезервирован для обозначения пикселов, для которых не измеряется неравенство, так называемый никаких данных. Таким образом, несоответствие изображения содержит 1024 уровней неравенства. Так как глубина обратно пропорциональна несоответствие разрешения глубины и обратно, связанные с уровнем неравенства. То есть, глубина резкости не является постоянной и уменьшается с увеличением расстояния до датчика. Например, на расстоянии 2 м один уровень неравенства соответствует разрешением 1 см глубиной, а в 5 метров один несоответствие уровню соответствует примерно 7 см, глубина разрешение.

4. Экспкрименты и результаты

Эксперименты проводились в первую очередь для того, чтобы определить параметры калибровки датчика и затем исследовать систематические и случайные ошибки в глубине данных. В следующих разделах описаны испытания и приведены результаты.

4.1 Результаты калибровки

Стандартная калибровка камеры была проведена для определения внутренних параметров инфракрасной камеры с помощью программного обеспечения Photomodeler ®. Всего 8 изображений были приняты целевой образец под разными углами. Чтобы избежать нарушения лазерных пятен на снимках отверстие лазерного излучателя была покрыта куском непрозрачного ленты. На рисунке 3 показано одно из изображений, используемых в калибровке. В таблице 1 приведены результаты калибровки. Общая точность калибровки в пространстве изображения было 0,395 пикселей, RMS точечных маркировки остатков после уравнивание. Рисунок 3 показывает калибровку остатков построения на одном из изображений.

Для определения параметров, входящих в неравенство углубленного соотношение (уравнение 5) значения глубины измерялись на плоской поверхности в восемь разных расстояний до датчика с помощью измерительной ленты. Обратная измеренных расстояний затем были нанесены на соответствующие нормированные различия наблюдаются с помощью датчика, см. Рисунок 4. Как видно, соотношение линейной, как мы ожидали от математической модели приведен в уравнении (5). Простой наименьших квадратов линейной регрессии обеспечивает параметры этой линейной зависимости, которые затем используются для расчета глубины от наблюдаемого нормированного неравенства. Наклон и перехват наиболее подходящую линию оказалось соответственно-2.85e-5 (см-2) и 0,03 (см-1).

Таблица 1. Калибровка параметров инфракрасной камеры

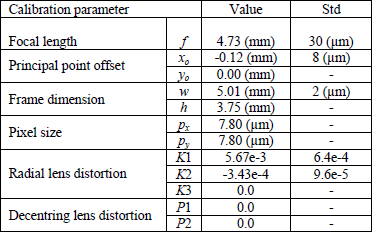
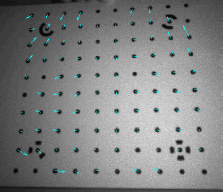
Рисунок 3. Инфракрасное изображение модели калибровки и остаточных векторов калибровки. Векторы увеличены для лучшей видимости.

Рисунок 4. Линейная зависимость нормированной дисперсии с обратной глубиной.

4.2 Сравнение с высокоточным лазерным облаком точек

Для исследования систематических ошибок в Kinect данных было проведено сравнение с облаками точек получить высококачественный лазерный сканер. Облако Kinect точка была получена из несоответствия изображения с помощью уравнения (4) и (5) и параметры калибровки на предыдущем шаге.Точка лазерного сканера облако было получено и той же сцены с помощью калиброванного FARO LS880 лазерного сканера. Номинальная точность диапазона лазерного сканера составляет 0,7 мм для объектов с высокой отражающей способностью на расстоянии 10 м от сканера (Фаро, 2007).Среднее расстояние точки точка лазерного сканера облако на поверхности, перпендикулярной направлению диапазона (а также оптической оси ИК-камеры Kinect) 5 мм. Поэтому было предположить, что точка лазерного сканера облако является достаточно точным и плотным, чтобы служить в качестве эталона для оценки точности Kinect шума. В отсутствие каких-либо систематических ошибок, среднее расхождение между двумя облаками точки как ожидается, будет близка к нулю.

Регистрация точности важна, потому что любой регистрации ошибка может быть неверно истолкована как ошибка в Kinect шума. Для достижения максимальной точности двух методов регистрации были протестированы. Первый способ состоял в руководстве грубо выравнивание следует штраф регистрация с использованием итерационного ближайший пункт (НКП) алгоритм (БИК и Маккей, 1992). Для того, чтобы МСП более эффективным вариантом предложенного Pulli (1999) последовал в которых 200 случайно выбранных соответствия (ближайших точек) с отказом в размере 40% были использованы. Во втором методе две примерно краю облаков точек были разделены на плоских поверхностях и 20 соответствующих сегментов выбраны вручную. Затем, надежный монтаж плоскости, используя RANSAC (Фишлер и Боллс, 1981;. Санде и др., 2010) была применена для получения плоскости параметров и лежащий внутри очков.Регистрация Затем был проведен за счет минимизации расстояния от точек в одной точке облака в соответствующие плоскости в другой шум.

В обоих случаях регистрации оцениваемых параметров преобразования состояла из 3-вращение и 3D-трансляции. Чтобы выявить возможную разницу между шкалой облака точек 1/3 регистрация осуществляется с помощью самолета на основе метода дополнены параметр масштаба.

В таблице 2 приведены регистрации остатков, относящихся к трем методам. На рисунке 5 показано окно сюжет регистрации остатков из трех методов. Как видно плоскости на основе метода выполняют так же, как урожайность меньше остатков по сравнению с методом ICP со случайными соответствия. Кроме того, параметр масштаба получил от третьих регистрации оказалось 1,002. Наибольший эффект такого масштаба в самой дальней точке облака точек составляет 1 см, что является незначительным по сравнению с случайная ошибка и глубина резкости данных. Таким образом, можно сделать вывод, что Kinect помутнения имеет тот же масштаб, как облако точек лазерного сканера.

Для сравнения результат плоскости на основе регистрации без масштабных параметров был использован. В общей сложности 1000 очков были выбраны случайным образом из Kinect помутнения и для каждой точки ближайшего соседа был найден в облака точек лазерного сканера. Это ближайшая точка пар стали основой для оценки точности Kinect помутнения. Было, однако, считать, что точка пары могут содержать неверные соответствия, потому что два датчика была несколько иной угол обзора и, следовательно, области, которые не могли быть замечены один датчик может быть захвачен другим, и наоборот. На рисунке 6 показаны два облака точек и ближайших пары точка.

Таблица 2. Регистрация остатков по трем методам.

	Min (cm)	Mean (cm)	Median (cm)	Std (cm)	Max (cm)
point-point distances (icp)	0.2	2.9	1.9	2.6	11.7
point-plane distances with scale	0.0	1.8	1.7	1.2	7.3
point-plane distances w/o scale	0.0	1.8	1.7	1.2	6.8

Figure 5. Box plot of registration results of the three methods. The boxes show the 25th and 75th percentiles of residuals, red lines are medians, whiskers are minimum and maximum, and black dots are large residuals identified as outliers.

Рисунок 6. Сравнение Kinect облако точек (голубой) с облаков точек, полученных FARO LS880 лазерного сканера (белый). Чем больше точек образцы случайным образом выбирается из Kinect данные (синий) и их ближайшие точки лазерного сканера данных (красный).

На рисунке 7 показана гистограмма расхождения между точкой пары X, Y и Z. В таблице 3 приведены статистические данные, связанные с этим противоречия.Среднее и среднее расхождения близки к нулю в Y и Z, но немного больше в X.

На рисунке 8 показано распределение расхождения в плоскости XZ. Цвета представляют евклидово расстояние между точками пары сантиметров. Обратите внимание, что в целом расхождения между точкой пар меньше, на расстоянии ближе к датчику (меньше Z) и больше дальше. Это то, что мы ожидаем от теоретической модели случайных ошибок. Также обратите внимание на большие расхождения на стороне коробки рядом с датчиком. Это вызвано меньшей точностью точек за счет ориентации на поверхности датчика.Измерений и лазерным сканером и Kinect менее точны при больших углах падения лазерного луча на поверхности мишени. В общем, сравнение двух облаков точек показывает, что более 80% пар точек меньше 3 см друг от друга.

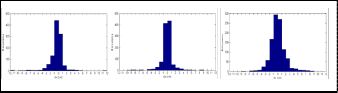
Рисунок 7. Гистограмма расхождений между точкой пары X, Y и Z направлением.

Таблица 3. Статистика расхождений между точками пары.

	dx	dy	dz
Mean (cm)	-0.4	-0.1	0.0
Median (cm)	-0.2	0.0	-0.1
Standard deviation (cm)	1.5	1.3	1.9
Interquartile range (cm)	1.0	0.7	1.8
Percentage in [-0.5cm, 0.5cm]	52.8	61.4	29.0
Percentage in [-1.0 cm, 1.0 cm]	71.8	79.8	52.9
Percentage in [-2.0 cm, 2.0 cm]	88.4	91.3	79.5

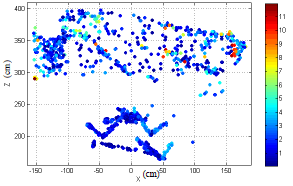
Рисунок 8. Распределение точка пара расстояния в плоскости XZ.

4.3 Тест установки плоскости

Плоская поверхность двери была измерена на различных расстояниях от 0,5 м до 5,0 м (радиус действия датчика) с 0,5 м интервалом.

В каждой полученном облаке точек же часть двери была выбрана, и плоскость была установлена на выбранные точки. RANSAC метод установки плоскости был использован, чтобы избежать влияния выбросов. На рисунке 9 показано измерения установки.

Поскольку во всех измерениях выбранной плоской поверхности составляет примерно перпендикулярно оптической оси датчика остатков процедуры установки плоскости указанных случайных ошибок в глубине компонент точек. Для оценки этих случайных ошибок равное количество образцов (4500 образцов) были выбраны случайным образом от каждой плоскости, а стандартное отклонение остатков была рассчитана на отобранных проб. На рисунке 10 показаны рассчитанные отклонения стандартный заговор против расстояние от плоскости датчика. Видно, что ошибки увеличить квадратично от нескольких миллиметров на 0,5 м до 4 см при максимальной дальности датчика. Кривая в красный цвет как нельзя лучше подойдет квадратичной кривой. Это подтверждает наши теоретические модели случайных ошибок (7) показывает, что случайная погрешность измерения глубины возрастает пропорционально квадрату расстояния от датчика.

На рисунке 11 (а) показано распределение остатков установка на плоскости на расстоянии 4 метров. Цвета представляют точку на плоскости расстояние в сантиметрах. Интересно, что распределение остатков не является полностью случайным, хотя ясно систематический характер, также не очевидна. На рисунке 11 (б) вид сбоку той же плоскости показано на рисунке. Как можно видеть, измерения глубины на плоскости не только под влиянием случайных ошибок, но и с низким разрешением глубины измерений. На расстоянии 4 метров глубины резкости составляет около 5 см. Сочетание случайных ошибок и низким разрешением глубины результатов измерения в представлении поверхности в несколько кусочков, как показано на рисунке 11 (б).

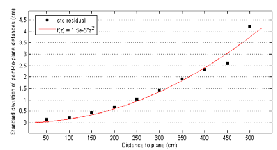
Рисунок 10. Стандартное отклонение плоскости установки остатков на разных расстояниях от плоскости датчика. Наилучшее - квадратичная кривая красного цвета.

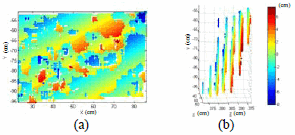
Рисунок 11. Плоскость установки остатка: (а) распределение остатков на плоскости на 4 метра расстояния до датчика, (б) вид сбоку точками показано влияние низким разрешением глубины. Цвета представляют расстояние до наиболее подходящей плоскости в сантиметрах.

5. Заключительные замечания

В работе представлены теоретические и экспериментальные данные, точность анализа глубины данных, полученных датчиком Kinect. Из результатов можно сделать следующие общие выводы :

- Облако точек откалиброваных датчиком Kinect не содержит больших систематических ошибок по сравнению с данными лазерного сканирования;

- Случайная погрешность измерения глубины квадратично растет с увеличением расстояния от датчиков и достигает 4 см при максимальной дальности;

- Плотность точек уменьшается с увеличением расстояния до датчика. Влияющим фактором является глубина резкости, которая является очень низкой на большом расстоянии (7 см на расстоянии до 5 м).

В общем, для отображения приложений данные должны быть получены на расстоянии от 1 до 3 м до сенсора. На больших расстояниях, качество данных деградирует в результате шума и низкого разрешения глубины измерений.

Рисунок 9. Плоской поверхности двери измеряется на разных расстояниях к датчику. Прямоугольники указывают область плоскости монтажа.

Благодарности

Я благодарен открытому сообществу Kinect и, в частности, Николя Буррусу из лаборатории робототехники за предостовление интерфейса с открытым исходным кодом для потоковой передачи данных Kinect.

Ссылки:

Besl, P.J., McKay, N.D., 1992. A method for registration of 3-D shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence 14, 239-256.
Breuer, P., Eckes, C., Muller, S., 2007. Hand gesture recognition with a novel IR time-of-flight range camera - a pilot study, in: Gagalowicz, A., Philips, W. (Eds.), Lecture Notes in Computer Science. Springer, Berlin, pp. 247-260.
Faro, 2007. Laser Scanner LS 880 Techsheet. http://faro.com/FaroIP/Files/File/Techsheets%20Download/U K_LASER_SCANNER_LS.pdf.PDF (accessed April 2011).
Fischler, M.A., Bolles, R.C., 1981. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM 24, 381-395.
Fraser, C.S., 1997. Digital camera self-calibration. ISPRS Journal of Photogrammetry and Remote Sensing 52, 149-159.
Freedman, B., Shpunt, A., Machline, M., Arieli, Y., 2010. Depth mapping using projected patterns. Prime Sense Ltd, United States.
Henry, P., Krainin, M., Herbst, E., Ren, X., Fox, D., 2010. RGB-D Mapping: Using Depth Cameras for Dense 3D Modeling of Indoor Environments, Proc. of International Symposium on Experimental Robotics (ISER), Delhi, India.
Kahlmann, T., Ingensand, H., 2008. Calibration and development for increased accuracy of 3D range imaging cameras. Journal of Applied Geodesy 2, 1-11.
Kahlmann, T., Remondino, F., Ingensand, H., 2006. Calibration for increased accuracy of the range imaging camera SwissRanger, ISPRS Commission V Symposium 'Image Engineering and Vision Metrology', Dresden, Germany, pp. 136-141.
Lichti, D.D., 2008. Self-calibration of a 3D range camera, International Archives of the Photogrammetry Remote Sensing and Spatial Information Sciences, Vol. XXXVII, Part B5, Beijing, China, pp. 927-932.
Microsoft, 2010. Kinect. http://www.xbox.com/en-us/kinect/ (accessed 27 March 2011).
PrimeSense, 2010. http://www.primesense.com/ (accessed 27 March 2011).
Pulli, K., 1999. Multiview Registration for Large Data Sets, Second International Conference on 3D Digital Imaging and Modeling, Ottawa, Canada.
Rusinkiewicz, S., Levoy, M., 2001. Efficient variants of the ICP algorithm. IEEE Computer Soc, Los Alamitos.
Sande, C.v.d., Soudarissanane, S., Khoshelham, K., 2010. Assessment of Relative Accuracy of AHN-2 Laser Scanning Data Using Planar Features. Sensors 10, 8198-8214.