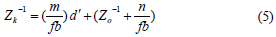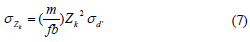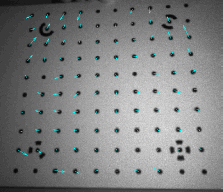Key words: Accuracy, error, range imaging, range camera, RGB-D, laser scanning, point cloud, calibration, indoor mapping.
Abstract:
This paper presents an investigation of the geometric quality of depth data obtained by the Kinect sensor. Based on the mathematical model of depth measurement by the sensor a theoretical error analysis is presented, which provides an insight into the factors influencing the accuracy of the data. Experimental results show that the random error of depth measurement increases with increasing distance to the sensor, and ranges from a few millimetres up to about 4 cm at the maximum range of the sensor. The accuracy of the data is also found to be influenced by the low resolution of the depth measurements.
1. Introduction
Low-cost range sensors are an attractive alternative for expensive laser scanners in application areas such as indoor mapping, surveillance, robotics and forensics. A recent development in consumer-grade range sensing technology is Microsoft’s Kinect sensor (Microsoft, 2010). Kinect was primarily designed for natural interaction in a computer game environment (PrimeSense, 2010). However, the characteristics of the data captured by Kinect have attracted the attention of researchers from the field of mapping and 3d modelling. A recent demonstration of the potential of Kinect for 3d modelling of indoor environments can be seen in the work of Henry et al., (2010).
The Kinect sensor captures depth and colour images simultaneously at a frame rate of about 30 fps. The integration of depth and colour data results in a coloured point cloud that contains about 300,000 points in every frame. By registering the consecutive depth images one can obtain an increased point density, but also create a complete point cloud of an indoor environment possibly in real time. To reach the full potential of the sensor for mapping applications an analysis of the systematic and random errors of the data is necessary. The correction of systematic errors is a prerequisite for the alignment of the depth and colour data, and relies on the identification of the mathematical model of depth measurement and the calibration parameters involved. The characterization of random errors is important and useful in further processing of the depth data, for example in weighting the point pairs in the registration algorithm (Rusinkiewicz and Levoy, 2001).
Since Kinect is a recent development – it was released in November 2010 – little information about the geometric quality of its data is available. The geometric investigation and calibration of similar range sensors, such as the SwissRanger, has been the topic of several previous works (Breuer et al.,2007; Kahlmann and Ingensand, 2008; Kahlmann et al., 2006; Lichti, 2008). However, the depth measurement principle in Kinect is different from that of SwissRanger.
In this paper our primary focus is on the depth data. The objective of the paper is to provide an insight into the geometric quality of the Kinect depth data through an analysis of the accuracy and density of the points. We present a mathematical model for obtaining 3d object coordinates from the raw image measurements, and discuss the calibration parameters involved in the model. Further, a theoretical random error model is derived and verified by an experiment.
The paper proceeds with a description of the depth measurement principle, the mathematical model and the calibration parameters in Section 2. In Section 3, the error sources are discussed, and a theoretical error model is presented. In Section 4, the models are verified through a number of experiments and the results are discussed. The paper concludes with some remarks in Section 5.
2. Principle of depth measurement by triangulation
The Kinect sensor consists of an infrared laser emitter, an infrared camera and an RGB camera. The inventors describe the measurement of depth as a triangulation process (Freedman et al., 2010). The laser source emits a single beam which is split into multiple beams by a diffraction grating to create a constant pattern of speckles projected onto the scene. This pattern is captured by the infrared camera and is correlated against a reference pattern. The reference pattern is obtained by capturing a plane at a known distance from the sensor, and is stored in the memory of the sensor. When a speckle is projected on an object whose distance to the sensor is smaller or larger than that of the reference plane the position of the speckle in the infrared image will be shifted in the direction of the baseline between the laser projector and the perspective centre of the infrared camera. These shifts are measured for all speckles by a simple image correlation procedure, which yields a disparity image. For each pixel the distance to the sensor can then be retrieved from the corresponding disparity, as described in the next section.
Figure1 illustrates the depth measurement from the speckle pattern.

Figure 1. Left: infrared image of the pattern of speckles projected on the object; Right: the resulting depth image.
2.1 Mathematical model
Figure 2 illustrates the relation between the distance of an object point k to the sensor relative to a reference plane and the measured disparity d. To express the 3d coordinates of the object points we consider a depth coordinate system with its origin at the perspective centre of the infrared camera. The Z axis is orthogonal to the image plane towards the object, the X axis perpendicular to the Z axis in the direction of the baseline b between the infrared camera centre and the laser projector, and the Y axis orthogonal to X and Z making a right handed coordinate system.
Assume that an object is on the reference plane at a distance Zo to the sensor, and a speckle on the object is captured on the image plane of the infrared camera. If the object is shifted closer to (or further away from) the sensor the location of the speckle on the image plane will be displaced in the X direction. This is measured in image space as disparity d corresponding to a point k in the object space. From the similarity of triangles we have:

and:

where Zk denotes the distance (depth) of the point k in object space, b is the base length, f is the focal length of the infrared camera, D is the displacement of the point k in object space, and d is the observed disparity in image space. Substituting D from (2) into (1) and expressing Zk in terms of the other variables yields:

Equation (3) is the basic mathematical model for the derivation of depth from the observed disparity provided that the constant parameters Zo, f, and b can be determined by calibration. The Z coordinate of a point together with f defines the imaging scale for that point. The planimetric object coordinates of each point can then be calculated from its image coordinates and the scale:
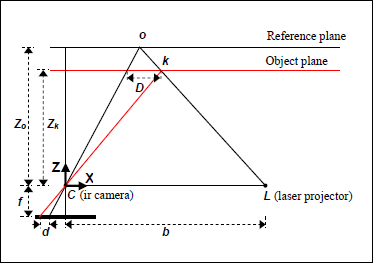
Figure 2. Schematic representation of depth-disparity relation.

where xk and yk are the image coordinates of the point, xo and yo are the coordinates of the principal point, and ?x and ?y are corrections for lens distortion, for which different models with different coefficients exist; see for instance (Fraser, 1997). Note that here we assume that the image coordinate system is parallel with the base line and thus with the depth coordinate system.
2.2 Calibration
As mentioned above, the calibration parameters involved in the mathematical model for the calculation of 3d coordinates from the raw image measurements include:
- focal length (f);
- principal point offsets (xo, yo);
- lens distortion coefficients (in ?x, ?y);
- base length (b);
- distance of the reference pattern (Zo).
In addition, we may consider a misalignment angle between the x-axis of the image coordinate system and the base line. However, this does not affect the calculation of the object coordinates if we define the depth coordinate system to be parallel with the image coordinate system instead of the base line. We may, therefore, ignore this misalignment angle.
From the calibration parameters listed above the first three can be determined by a standard calibration of the infrared camera. The determination of the base length and the reference distance is however complicated for the following reason. In practice, it is not possible to stream the actual measured disparities, probably due to bandwidth limitation. Instead, the raw disparity values are normalized between 0 and 2047, and streamed as 11 bit integers. Therefore, in Equation (3) d should be replaced with md’+n with d’ the normalized disparity and m, n the parameters of a (supposedly) linear normalization (in fact denormalization). Including these in Equation (3) and inverting it yields:
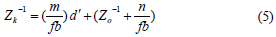
Equation (5) expresses a linear relation between the inverse depth of a point and its corresponding normalized disparity. By observing the normalized disparity for a number of object points (or planes) at known distances to the sensor the coefficients of this linear relation can be estimated in a least-squares fashion. However, the inclusion of the normalization parameters does not allow determining b and Zo separately.
2.3 Integration of depth and colour
The integration of the depth and colour data requires the orientation of the RGB camera relative to the depth coordinate system. Since we defined the depth coordinate system at the perspective centre of the infrared camera we can perform the orientation by a stereo calibration of the two cameras. The parameters to be estimated include three rotations between the camera coordinate system of the RGB camera and that of the infrared camera, and the 3d position of the perspective centre of the RGB camera in the coordinate system of the infrared camera. In addition, the interior orientation parameters of the RGB camera, i.e. the focal length, principal point offsets and the lens distortion parameters must be estimated. Once these parameters are known we can project every 3d point from the point cloud to the RGB image, interpolate the colour, and assign it to the point.
3. Depth accuracy and point density
Accuracy and point density are two important measures for evaluating the quality of a point cloud. In the following sections factors influencing the accuracy and density of Kinect data are discussed, and a theoretical random error model is presented.
3.1 Error sources
Error and imperfection in the Kinect data may originate from three main sources:
- the sensor;
- the measurement setup;
- the properties of object surface.
The sensor errors, for a properly functioning device, mainly refer to inadequate calibration and inaccurate measurement of disparities. Inadequate calibration and/or error in the estimation of the calibration parameters lead to systematic error in the object coordinates of individual points. Such systematic errors can be eliminated by a proper calibration as described in the previous section. Inaccurate measurement of disparities within the correlation algorithm and round-off errors during normalization result in errors, which are most likely of a random nature.
Errors caused by the measurement setup are mainly related to the lighting condition and the imaging geometry. The lighting condition influences the correlation and measurement of disparities. In strong light the laser speckles appear in low contrast in the infrared image, which can lead to outliers or gap in the resulting point cloud. The imaging geometry includes the distance to the object and the orientation of the object surface relative to the sensor. The operating range of the sensor is between 0.5 m to 5.0 m according to the specifications, and, as we will see in the following section, the random error of depth measurement increases with increasing distance to the sensor. Also, depending on the imaging geometry, parts of the scene may be occluded or shadowed. In Figure 1, the right side of the box is occluded as it cannot be seen by the infrared camera though it may have been illuminated by the laser pattern. The left side of the box is shadowed because it is not illuminated by the laser but is captured in the infrared image. Both the occluded areas and shadows appear as gaps in the point cloud.
The properties of the object surface also impact the measurement of points. As it can be seen in Figure 1 smooth and shiny surfaces that appear overexposed in the infrared image (the lower part of the box) impede the measurement of disparities, and result in a gap in the point cloud.
3.2 Theoretical random error model
Assuming that in Equation (5) the calibration parameters are determined accurately and that d’ is a random variable with a normal distribution we can propagate the variance of the disparity measurement to obtain the variance of the depth measurement as follows:

After simplification this yields the following expression for the standard deviation of depth:
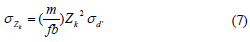
with ?d’ and ?Zk respectively the standard deviation of the measured normalized disparity and the standard deviation of the calculated depth. Equation 7 basically expresses that the random error of depth measurement is proportional to the square distance from the sensor to the object. Since depth is involved in the calculation of the planimetric coordinates, see Equation 4, we may expect the error in X and Y to be also a second order function of depth.
3.3 Point density
The resolution of the infrared camera, i.e. the pixel size, determines the point spacing of the depth data on the XY plane (perpendicular to camera axis). Since each depth image contains a constant 640x480 pixels the point density will decrease with increasing distance of the object surface from the sensor. Considering the point density as the number of points per unit area, while the number of points remains constant the area is proportional to the square distance from the sensor. Therefore, the point density is inversely proportional to the square distance from the sensor, that is:

The depth resolution is determined by the number of bits per pixel used to store the disparity measurements. The Kinect disparity measurements are stored as 11-bit integers, where 1 bit is reserved to mark the pixels for which no disparity is measured, so-called no data. Therefore, a disparity image contains 1024 levels of disparity. Since depth is inversely proportional to disparity the resolution of depth is also inversely related to the levels of disparity. That is, the depth resolution is not constant and decreases with increasing distance to the sensor. For instance, at a range of 2 meters one level of disparity corresponds to 1 cm depth resolution, whereas at 5 meters one disparity level corresponds to about 7 cm depth resolution.
4. Experiments and results
Experiments were carried out to first determine the calibration parameters of the sensor and then investigate the systematic and random errors in the depth data. The following sections describe the tests and discuss the results.
4.1 Calibration results
A standard camera calibration was performed to determine the interior parameters of the infrared camera using the Photomodeler® software. A total of 8 images were taken of a target pattern from different angles. To avoid the disturbance of the laser speckles in the images the aperture of the laser emitter was covered by a piece of opaque tape. Figure 3 shows one of the images used in the calibration. Table 1 summarizes the calibration results. The overall calibration accuracy in image space was 0.395 pixels as the RMS of point marking residuals after the bundle adjustment. Figure 3 also shows the calibration residuals plotted on one of the images.
To determine the parameters involved in the disparity-depth relation (Equation 5) depth values were measured for a planar surface at eight different distances to the sensor using a measuring tape. The inverse of the measured distances were then plotted against the corresponding normalized disparities observed by the sensor, see Figure 4. As it can be seen the relation is linear as we expected from the mathematical model given in Equation (5). A simple least-squares linear regression provides the parameters of this linear relation, which are then used to calculate depth from the observed normalized disparity. The slope and intercept of the best-fit line was found to be respectively -2.85e-5 (cm-2) and 0.03 (cm-1).
Table 1. Calibration parameters of the infrared camera
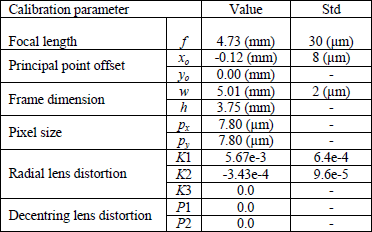
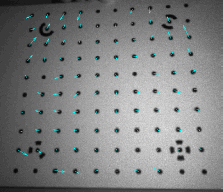
Figure 3. Infrared image of the calibration pattern and the residual vectors of calibration. The vectors are enlarged for better visibility.

Figure 4. Linear relation of normalized disparity with inverse depth.
4.2 Comparison with a high-end laser scanner point cloud
To investigate the systematic errors in Kinect data a comparison was made with a point cloud obtained by a high-end laser scanner. The Kinect point cloud was obtained from the disparity image using Equations (4) and (5) and the calibration parameters from the previous step. The laser scanner point cloud was obtained of the same scene by a calibrated FARO LS880 laser scanner. The nominal range accuracy of the laser scanner is 0.7 mm for highly reflective objects at a distance of 10 m to the scanner (Faro, 2007). The average point spacing of the laser scanner point cloud on a surface perpendicular to the range direction (and also the optical axis of the infrared camera of Kinect) was 5 mm. It was therefore assumed that the laser scanner point cloud is sufficiently accurate and dense to serve as reference for the accuracy evaluation of the Kinect point cloud. In the absence of any systematic errors the mean of discrepancies between the two point clouds is expected to be close to zero.
To enable this analysis, first, an accurate registration of the two point clouds is necessary. The registration accuracy is important because any registration error may be misinterpreted as error in the Kinect point cloud. To achieve the best accuracy two registration methods were tested. The first method consisted of a manual rough alignment followed by a fine registration using the iterative closest point (ICP) algorithm (Besl and McKay, 1992). To make ICP more efficient a variant suggested by Pulli (1999) was followed in which 200 randomly selected correspondences (closest points) with a rejection rate of 40% were used. In the second method the two roughly-aligned point clouds were segmented into planar surfaces and 20 corresponding segments were manually selected. Then, a robust plane fitting using RANSAC (Fischler and Bolles, 1981; Sande et al., 2010) was applied to obtain plane parameters and the inlying points. The registration was then performed by minimizing the distances from the points in one point cloud to their corresponding planes in the other point cloud.
In both registrations the estimated transformation parameters consisted of a 3d rotation and a 3d translation. To reveal a possible scale difference between the point clouds a third registration was performed using the plane-based method augmented with a scale parameter.
Table 2 summarizes the registration residuals pertaining to the three methods. Figure 5 shows a box plot of the registration residuals of the three methods. As it can be seen the plane-based methods perform similarly both yielding smaller residuals as compared to the ICP method with random correspondences. Furthermore, the scale parameter obtained from the third registration was found to be 1.002. The largest effect of such scale on the furthest point of the point cloud is 1 cm, which is negligible as compared to the random error and depth resolution of the data. We may therefore conclude that the Kinect point cloud has the same scale as the laser scanner point cloud.
For the comparison the result of the plane-based registration without the scale parameters was used. A total of 1000 points were randomly selected from the Kinect point cloud and for each point the nearest neighbour was found in the laser scanner point cloud. These closest point pairs were the basis for evaluating the accuracy of the Kinect point cloud. It was however considered that the point pairs may contain incorrect correspondences because the two sensors had slightly different viewing angles and therefore areas that could not be seen by one sensor might be captured by the other and vice versa. Figure 6 shows the two point clouds and the closest point pairs.
Table 2. Registration residuals of the three methods.
| Min (cm) | Mean (cm) | Median (cm) | Std (cm) | Max (cm) |
point-point distances (icp) | 0.2 | 2.9 | 1.9 | 2.6 | 11.7 |
point-plane distances with scale | 0.0 | 1.8 | 1.7 | 1.2 | 7.3 |
point-plane distances w/o scale | 0.0 | 1.8 | 1.7 | 1.2 | 6.8 |

Figure 5. Box plot of registration results of the three methods. The boxes show the 25th and 75th percentiles of residuals, red lines are medians, whiskers are minimum and maximum, and black dots are large residuals identified as outliers.

Figure 6. Comparison of Kinect point cloud (cyan) with the point cloud obtained by the FARO LS880 laser scanner (white). The larger points are samples randomly selected from the Kinect data (blue) and their closest point in the laser scanner data (red).
Figure 7 shows the histograms of discrepancies between the point pairs in X, Y and Z. Table 3 lists the statistics related to these discrepancies. The mean and median discrepancies are close to zero in Y and Z, but slightly larger in X.
Figure 8 shows the distribution of the discrepancies in the X-Z plane. The colours represent the Euclidean distance between the point pairs in centimetres. Note that in general the discrepancies between the point pairs are smaller at closer distance to the sensor (smaller Z) and larger further away. This is what we expect from the theoretical random error model. Also, note the larger discrepancies on the side of a box close to the sensor. These are caused by the lower accuracy of the points due the orientation of the surface towards the sensors. The measurements from both the laser scanner and Kinect are less accurate at large incidence angles of the laser beams to the target surface. In general, the comparison of the two point clouds shows that more than 80% of the point pairs are less than 3 cm apart.
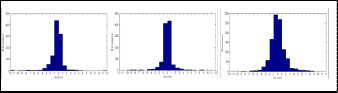
Figure 7. Histograms of discrepancies between the point pairs in X, Y and Z direction.
Table 3. Statistics of discrepancies between point pairs.
| dx | dy | dz |
Mean (cm) | -0.4 | -0.1 | 0.0 |
Median (cm) | -0.2 | 0.0 | -0.1 |
Standard deviation (cm) | 1.5 | 1.3 | 1.9 |
Interquartile range (cm) | 1.0 | 0.7 | 1.8 |
Percentage in [-0.5cm, 0.5cm] | 52.8 | 61.4 | 29.0 |
Percentage in [-1.0 cm, 1.0 cm] | 71.8 | 79.8 | 52.9 |
Percentage in [-2.0 cm, 2.0 cm] | 88.4 | 91.3 | 79.5 |
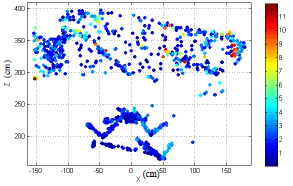
Figure 8. Distribution of point pair distances in the X-Z plane.
4.3 Plane fitting test
To verify the relation between the random error and the distance to the sensor a plane fitting test was carried out. The planar surface of a door was measured at various distances from 0.5 m to 5.0 m (the operation range of the sensor) with 0.5 m intervals.
In each resulting point cloud a same part of the door was selected and a plane was fitted to the selected points. The RANSAC plane fitting method was used to avoid the influence of outliers. Figure 9 shows the measurement setup.
Since in all measurements the selected planar surface was approximately perpendicular to the optical axis of the sensor the residuals of the plane fitting procedure indicated the random errors in the depth component of the points. To evaluate these random errors an equal number of samples (4500 samples) were randomly selected from each plane, and the standard deviation of the residuals was calculated over the selected samples. Figure 10 shows the calculated standard deviations plotted against the distance from the plane to the sensor. It can be seen that the errors increase quadratically from a few millimetres at 0.5 m distance to about 4 cm at the maximum range of the sensor. The curve in red colour is the best fit quadratic curve. This verifies our theoretical random error model (7) showing that the random error of depth measurements increases with the square distance from the sensor.
Figure 11 (a) shows the distribution of the fitting residuals on the plane at 4 m distance. The colours represent point to plane distances in centimetres. Interestingly, the distribution of the residuals is not completely random, though a clear systematic pattern is also not evident. In Figure 11 (b) a side view of the same plane is shown. As it can be seen, the depth measurement on the plane is not only influenced by the random errors but also by the low resolution of depth measurements. At 4 meters distance the depth resolution is about 5 cm. The combination of random errors and low resolution of the depth measurement results in a representation of the surface in several slices as shown in Figure 11 (b).
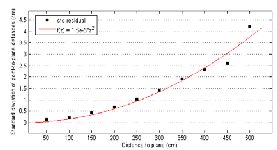
Figure 10. Standard deviation of plane fitting residuals at different distances of the plane to the sensor. The best fit quadratic curve is plotted in red.
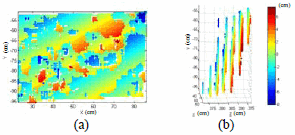
Figure 11. Plane fitting residuals: (a) distribution of residuals on the plane at 4 meters distance to the sensor; (b) a side view of the points showing the effect of low depth resolution. Colours represent distance to the best-fit plane in centimetres.
5. Concluding remarks
The paper presented a theoretical and experimental accuracy analysis of depth data acquired by the Kinect sensor. From the results the following general conclusions can be drawn:
- The point cloud of a properly calibrated Kinect sensor does not contain large systematic errors when compared with a laser scanning data;
- The random error of depth measurements increases quadratically with increasing distance from the sensor and reaches 4 cm at the maximum range;
- The density of points also decreases with increasing distance to the sensor. An influencing factor is the depth resolution, which is very low at large distance (7 cm at the maximum range of 5 m).
In general, for mapping applications the data should be acquired within 1~3 m distance to the sensor. At larger distances, the quality of the data is degraded by the noise and low resolution of the depth measurements.

Figure 9. The planar surface of a door measured at different distances to the sensor. The boxes show the plane fitting area.
Acknowledgements
I am grateful to the Open Kinect community and in particular Nicolas Burrus of the Robotics Lab for providing an open-source interface to stream the Kinect data.
References:
Besl, P.J., McKay, N.D., 1992. A method for registration of 3-D
shapes. IEEE Transactions on Pattern Analysis and Machine
Intelligence 14, 239-256.
Breuer, P., Eckes, C., Muller, S., 2007. Hand gesture
recognition with a novel IR time-of-flight range camera - a
pilot study, in: Gagalowicz, A., Philips, W. (Eds.), Lecture
Notes in Computer Science. Springer, Berlin, pp. 247-260.
Faro, 2007. Laser Scanner LS 880 Techsheet.
http://faro.com/FaroIP/Files/File/Techsheets%20Download/U
K_LASER_SCANNER_LS.pdf.PDF (accessed April 2011).
Fischler, M.A., Bolles, R.C., 1981. Random sample consensus:
a paradigm for model fitting with applications to image
analysis and automated cartography. Communications of the
ACM 24, 381-395.
Fraser, C.S., 1997. Digital camera self-calibration. ISPRS
Journal of Photogrammetry and Remote Sensing 52, 149-159.
Freedman, B., Shpunt, A., Machline, M., Arieli, Y., 2010.
Depth mapping using projected patterns. Prime Sense Ltd,
United States.
Henry, P., Krainin, M., Herbst, E., Ren, X., Fox, D., 2010.
RGB-D Mapping: Using Depth Cameras for Dense 3D
Modeling of Indoor Environments, Proc. of International
Symposium on Experimental Robotics (ISER), Delhi, India.
Kahlmann, T., Ingensand, H., 2008. Calibration and
development for increased accuracy of 3D range imaging
cameras. Journal of Applied Geodesy 2, 1-11.
Kahlmann, T., Remondino, F., Ingensand, H., 2006. Calibration
for increased accuracy of the range imaging camera
SwissRanger, ISPRS Commission V Symposium 'Image
Engineering and Vision Metrology', Dresden, Germany, pp.
136-141.
Lichti, D.D., 2008. Self-calibration of a 3D range camera,
International Archives of the Photogrammetry Remote
Sensing and Spatial Information Sciences, Vol. XXXVII,
Part B5, Beijing, China, pp. 927-932.
Microsoft, 2010. Kinect. http://www.xbox.com/en-us/kinect/
(accessed 27 March 2011).
PrimeSense, 2010. http://www.primesense.com/ (accessed 27
March 2011).
Pulli, K., 1999. Multiview Registration for Large Data Sets,
Second International Conference on 3D Digital Imaging and
Modeling, Ottawa, Canada.
Rusinkiewicz, S., Levoy, M., 2001. Efficient variants of the ICP
algorithm. IEEE Computer Soc, Los Alamitos.
Sande, C.v.d., Soudarissanane, S., Khoshelham, K., 2010.
Assessment of Relative Accuracy of AHN-2 Laser Scanning
Data Using Planar Features. Sensors 10, 8198-8214.