Реферат
Обробка
багатопараметричних даних вимірювань в
інформаційних системах захисту інформації
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження
- 3. Огляд досліджень та розробок
- 3.1 Огляд міжнародних джерел
- 3.2 Огляд національних та локальних джерел
- 4. Метод обробки багатопараметричних даних вимірювань
- Висновки
- Перелік посилань
Вступ
У процесі проектування системи літального апарату (ЛА) стає задача оптимального синтезу, тобто потрібно обрати структуру і параметри системи, що забезпечують її оптимальну якість.
Складність математичного опису систем ЛА, не стаціонарність і нелінійність процесів в ній, випадковість факторів, що діють на ЛА, обумовлюють складність задачі і не дозволяють створити строгий в математичному сенсі метод оптимального синтезу. Тому в процесі проектування вирішення задачі синтезу розпадається на ряд послідовних етапів і являє собою ітеративний процес з характерним для кожного етапу циклом – теорія, розрахунки, експеримент, аналіз. Саме через неможливість отримання адекватного теоретичного опису приблизно 40% усіх проблем, що виникають вирішуються за допомогою експериментальних випробувань. Але через складність і високу вартість ЛА виготовляти великі партії об’єктів для випробувань недоцільно. Для підвищення ефективності літних випробувань і зменшення матеріальних витрат на їх проведення, потрібно забезпечити вимірювання найбільш інформативних параметрів і використання високоточних систем вимірювання. Усі параметри руху ЛА можна розділити на 4 групи [1]:
- ті, що характеризують положення і переміщення центру мас об’єкта відносно різних систем відліку (координати об’єкту, його лінійна швидкість і прискорення);
- ті, що показують переміщення об’єкта відносно його центру мас (кути курсу, тангажу і крену, кути атаки і т.д.);
- ті, що характеризують функціонування бортових систем (тиск, температура, електричні величини);
- характеристики зовнішнього середовища (тиск, вологість, температура).
Перша група параметрів отримується системами зовнішньотраекторних вимірювань, параметри другою і третьої груп – бортовими і радіотелеметричними системами, четвертої групи – методами радіозондування.
Усі результати вимірювань синхронізуються службою єдиного часу. Але тут стає питання того, що не всі технічні засоби спроможні працювати в єдині моменти часу, а для точного аналізу даних всі вимірювання потрібно привести до єдиних моментів часу, тобто апроксимувати результати вимірів.
Внаслідок того, що при вимірюваннях неминучі перешкоди, а процеси, що досліджуються мають стохастичний характер, також потрібно передбачити можливість помилки та її відсів при обробці, чи якомога зменшити її вплив на кінцевий результат аналізу.
Тобто ми отримали задачу, вирішення якої допоможе нам підвищити ефективність випробувань ЛА. Задача складається з двох частин:
- Апроксимувати дані вимірювань для зведення їх до єдиних моментів часу [2];
- Згладити можливу помилку вимірювання і зменшити її вплив на результат роботи системи обробки [3,4].
1. Актуальність теми
В умовах швидкого розвитку технологій, коли якість та складність ЛА невпинно зростає, а траекторні вимірювання наближаються до меж своїх точностних можливостей, обумовлених, головним чином, станом атмосфери [5], особливо важливою стає розробка и застосування методів аналізу траекторної інформації [6], що базуються на використанні надмірних даних вимірювань для підвищення точності і достовірності результатів обробки [7].
2. Мета і задачі дослідження
Метою дослідження є розробка, моделювання [8], та, можливо, апробація алгоритму обробки багатопараметричних зовнішньотраекторних вимірювань на реальних даних вимірювань.
Основні задачі дослідження:
- Аналіз існуючих методів обробки зовнішньотраекторніх вимірювань;
- Вибір архітектури та основних концепцій нового методу обробки на базі поточних наукових досліджень [6, 9 – 13].
Об'єкт дослідження: методи обробки багатопараметричних даних зовнішньотраекторних вимірювань.
Предмет дослідження: об'єднання методів обробки часової та просторової надмірності.
3. Огляд досліджень та розробок
Питання обробки зовнішньотраєкторних вимірювань, як і довільних вимірювань взагалі, напряму пов'язане з методами апроксимації, інтерполяції, сгладжування та способами побудови математичних моделей. Проблеми їх аналізу та реалізації широко досліджуються як вченими закордоном, так і вітчизняними спеціалістами.
3.1 Огляд міжнародних джерел
Базовим методом апроксимації та регресіоного аналізу [14,15] є метод найменших квадратів, основний принцип якого полягає у мінімізації суми квадратів залишків регресії. За використання цього методу досліджуваний процес розкладається в n – мірному просторі у довільно обраному базисі. Базис може складатися з лінійнонезалежних (ЛНБФ) чи ортогональних (ОБФ) векторів. Використання ортогонального базису має декілька суттєвих переваг перед базисом ЛНБФ [16]. Проблема ефективної та швидкої побудови ОБФ досліджується багатьма закордонними авторами [15,17,18]. Також окремо можна виділити алгоритм побудови ОБФ із ЛНБФ, що являють собой степеневий ряд. Теоретичну основу заклав Форсайт (Forsythe G.E.) у 1957 році, коли у своїй статті [19] вперше описав, так звану, тричлену рекурентну формулу (Three – term recurrence relation [15]). Базовим та найбільш загальним методом побудови ОБФ є алгоритм Грама – Шмідта. Він та його модификації досліджуються в роботах Жюльєна Лангоу (Julien Langou) [20], але використовується він для розв'язання систем рівнянь з декількома векторами вільних членів [21].
3.2 Огляд національних та локальних джерел
Як одному з найпоширеніших методів обробки результатів експериментів, методу найменших квадратів присвячено багато статей, підручників та монографій [22–26].
У 1959 – 63 рр.. був розроблений узагальнений метод контролю траєкторій, що дозволив обробляти як мінімум даних вимірювань (три координати), так і всю сукупність просторово – надлишкової траєкторної інформації. Даний метод став основою кандидатської дисертації Н.Д. Огороднійчука [5,16].
Таким чином, створений метод обліку просторової надмірності даних вимірів, дозволяв використовувати інформацію від всіх вимірювальних пунктів. Але часова надмірність, що виникає при високому темпі знімання інформації, залишалася неврахованої. Тому подальшої завданням Н.Д. Огороднійчук поставив створення методу спільної реалізації просторової і часової надмірності.
В результаті, в 1974 році в Київському вищому військовому
авіаційному інженерному училищі Н.Д. Огороднійчук захистив
докторську дисертацію на тему Узагальнені методи і адаптивні
алгоритми обробки траєкторної інформації
.
Надалі в розвиток методів обробки зовнішньотраєкторної інформації величезний вклад внесли ад'юнкти Н.Д. Огороднійчука: П.І. Кушнарьов [27], В.В. Пасльон. Зокрема, були розроблені методи оперативного контролю і самоконтролю точності траєкторних вимірювальних засобів, детально досліджено ефективність адаптивних алгоритмів згладжування, досліджені алгоритми обробки збоїв і вплив автокореляції помилок вимірів на точність обробки траєкторної інформації. Було отримано 3 авторських свідоцтва на пристрої адаптивного оптимального згладжування даних.
Пізніше, з розвитком обчислювальної техніки, була вирішена задача оптимізації системи лямбда – ортогональних базисних функцій та досліджено можливості алгоритму спільного адаптивного нелінійного оптимального згладжування параметрів положення та руху, що володіють просторово – часової надмірністю [28].
4. Метод обробки багатопараметричних даних вимірювань
В роботі [10] проводиться моделювання процесу обробки багатопараметричних даних вимірювань, які мають просторову надмірність. Взагалі, функціонування узагальненою системи обробки з можливістю врахування часовою надмірності може бути представлена такою блок – схемою (рис. 1).
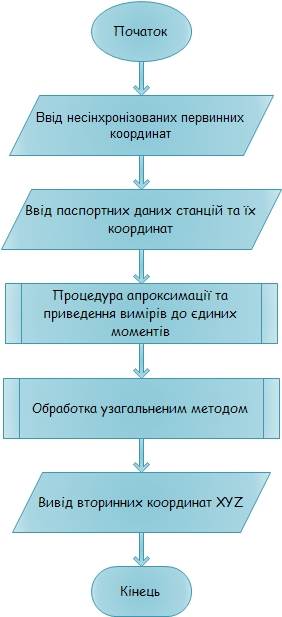
Рисунок 1. Блок – схема алгоритму
Узагальнений метод дає можливість отримати виграш в точності за рахунок кількості вимірювальних стацій (рис.2). Помилка розрахунку траєкторії зменшується з кількістю станцій. А якщо врахувати особливості функціонування кожної з них і оптимізувати їх взаємне місцезнаходження перед експериментальним вимірюванням [29], то помилку можна ще зменшити. Для перевірки роботи алгоритму моделювалась типова траєкторія польоту – Петля Нестерова. Для більшої наочності вихідна помилка помножена на 10.

Рисунок 2. Анімація. Залежність
помилки від кількості рівноточних станцій
(4 кадра, 2 секунди, ПЗ – MP Gif Animator)
Наступним етапом стане розробка алгоритму нелінійного
згладжування за допомогою ОБФ двох змінних. Зараз вже виконані
дослідження [12,30], які обгрунтовують можливість
застосування даного математичного апарату. Але стає питання: Яку
саме з наведених систем використовувати?
. Далі в роботі буде
наведено обгрунтування вибору однієї з клітково – матричних
структур, перевірка ортогональності ОБФ та моделювання процесу обробки.
Висновки
Магістерська робота присвячена актуальній науковій задачі спільної обробки багатопараметричних даних вимірювань, які мають просторову та часову надлишковість. На сьогодні:
- Розроблена загальна структура алгоритму обробки;
- На підставі виконаних досліджень обгрунтована можливість опису траекторії за допомогою ортогональних базисних функций двох змінних;
- Проведені експерименти щодо ефективності узагальненого методу обробки.
Подальші дослідження направлені на наступні аспекти:
- Дослідження та вибір однієї з клітково – матричних структур для опису траєкторії;
- Проведення чисельного моделювання роботи нового алгоритму та дослідження його властивостей та меж застосування.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.
Перелік посилань
- Кринецкий Е.И. Основы испытаний летательных аппаратов / Е.И. Кринецкий. – М.:Машиностроение,1989 р.
- Хлуднева А.В. Обработка избыточных данных измерений при несовпадении моментов измерений во времени / А.В. Хлуднева, М.В. Михайлов // Десята міжнародна молодіжна науково – практична конференція “Людина і космос”: Збірник тез. – Дніпропетровськ: НЦАОМУ, 2008 р.
- Фесенко Д.В. Устранение сбоев с помощью взвешенных приближений в адаптивних алгоритмах сглаживания / Д.В. Фесенко, М.В. Михайлов // Практика и перспективы развития партнерства в сфере высшей школы. Материалы восьмого научно-практического семинара. Донецк, 17-20 апреля 2007г. В 3-х томах. Т. 3 – Донецк , ДонНТУ, 2007 р. – с. 348 – 358.
- Травкин Р.В. Проблема исключения грубых ошибок из результатов внешнетраекторных измерений / Р.В. Травкин, В.В. Паслён // XIV Міжнародна молодіжна науково-практична конференція «Людина і Космос»: Збірник тез – Дніпропетровськ, 2012 р.
- Огороднийчук Н.Д. Обработка траекторной информации. Ч. I. / Н.Д. Огороднийчук – Киев: КВВАИУ, 1981. 141 с.
- Мотылев К.И. Обработка данных измерений, обладающих пространственной избыточностью / К.И. Мотылев, М.В. Михайлов, Е.В Гончаров // Таганрог: Изд–во ТРТУ, 2005. – с.260 – 262.
- Мотылев К.И.
Метод повышения точности обработки данных траекторных измерений /
К.И. Мотылев, В.В. Паслён // III Всероссийская
конференция
Радиолокация и радиосвязь
– ИРЭ РАН, 2009 г. - Шеннон Р.
Имитационное моделирование систем – Искусство и наука /
Р. Шеннон. – М.:
Мир
, 1978 р. – 420 с. - Мотылев К.И. Методы обработки данных измерений, обладающих пространственной и временной избыточностью / К.И. Мотылев , М.В. Михайлов , И.Л. Щербов , В.В. Паслён // Системные технологии. Региональный межвузовский сборник научных трудов. - Выпуск 8 (43). – Днепропетровск, 2006 – 149 с.
- Дрозда И.В. Реализация обобщенного метода обработки траекторной информации, обладающей пространственной избыточностью / И.В. Дрозда, В.В. Паслён, М.В. Михайлов // Вісник Дніпропетровського університету — Днепропетровск, ДНУ – 2009, Том 17, с. 3–7
- Мотылев К.И. Методы повышения точности определения вторичных координат маневрирующих объектов / К.И. Мотылев, В.В. Паслён // Донбас – 2020: перспективи розвитку очима молодих вчених: Матеріали V науково – практичної конференції. м. Донецьк, 25-27 травня 2010 р. – Донецьк, ДонНТУ Міністерства освіти і науки, 2010. – 973 с.
- Дрозда И.В.
О возможности применения базисных функций двух переменных в практике
траекторных измерений / И.В. Дрозда, Я.А. Савицкая,
А.В. Мильштейн //8 – я Международная молодежная
научно – техническая конференция
Современные проблемы радиотехники и телекоммуникаций
РТ – 2012 – Севастополь: 2012 г, с. 330 - Дрозда И.В.
Сравнение методов построения ортогональных базисных функций как
фундаментальной части алгоритмов сглаживания внешнетраекторных
измерений / И.В. Дрозда, В.В. Паслён // 6 –
я Международная молодежная научно – техническая конференция
Современные проблемы радиотехники и телекоммуникаций
РТ – 2010 – Севастополь: 2010 г, с. 380 - Себер Дж. Линейный
регрессионный анализ /
Дж. Себер. – М.:
Мир
, 1980 р. – 456 с. - Hamming R. W. Numerical Methods for Scientists and Engineers / R.W. Hamming. – New York: Dover Publications, Inc., 1986, c. 721
- Огороднийчук Н.Д. Обработка траекторной информации. Ч. IІ. / Н.Д. Огороднийчук – Киев: КВВАИУ, 1981. 230 с.
- Giraud Luc On the loss of orthogonality in the Gram-Schmidt orthogonalization process /Luc Giraud , Julien Langou , Miroslav Rozloznik// CERFACS – Advanced methods for the numerical simulation and the algorithmic solution [Электронный ресурс]. – Режим доступа: http://www.cerfacs.fr/algor/reports/2003/TR_PA_03_25.pdf
- Giraud Luc On the round – off error analysis of the Gram – Schmidt algorithm with reorthogonalization /Luc Giraud , Julien Langou , Miroslav Rozloznik // CERFACS – Advanced methods for the numerical simulation and the algorithmic solution [Электронный ресурс]. – Режим доступа: http://www.cerfacs.fr/algor/reports/2002/TR_PA_02_33.pdf
- Forsythe G.E. Generation and Use of Orthogonal Polynomials for Data – fitting with a Digital Computer,/. Soc. Ind. Appl. Math., vol. 5, no. 2, June, 1957; M. Ascherand G.E. Forsythe, SWAC Experiments on the Use of Orthogonal Polynomials for Data Fitting,/. Assoc. Computing Machinery, vol. 5, no. 1, January, 1958.
- Langou Julien PhD. Dissertation / Julien Langou //CERFACS – Advanced methods for the numerical simulation and the algorithmic solution [Электронный ресурс]. – Режим доступа: http://www.cerfacs.fr/algor/reports/Dissertations/TH_PA_03_24.pdf
- Langou Julien PhD. Thesis defence/ Julien Langou // CERFACS – Advanced methods for the numerical simulation and the algorithmic solution [Электронный ресурс]. – Режим доступа: http://www.cerfacs.fr/~langou/abstract-thesis.html
- Ліннік Ю.В. Метод наименьших квадратов и основы теории обработки наблюдений / Ю.В.Ліннік – М.: Физматгиз, 1962 р.
- Белов С.А. Численные методы линейной алгебры. Лабораторный практикум / С.А. Белов , Н.Ю. Золотих. – Нижний Новгород: Изд – во нижегородского госуниверситета им. Н.И. Лобачевского, 2005 р.
-
Паслён В.В.
Сглаживание и метод наименьших квадратов / В.В. Паслён //X
Міжнародна молодіжна науково – практична конференція
Людина і Космос
: Збірник тез – Дніпропетровськ: 2008. - Рао Р. Линейные
статистические методы и их применения / Р. Рао – М.:
Наука
, 1968. - Жданюк Б.Ф. Основы
статистической обработки наблюдений /
Б.Ф. Жданюк – М.:
Советское радио
, 1978. - Кушнарев П.И. Статистические методы контроля точноститраекторных измерительных средств / П.И. Кушнарев,Огороднийчук Н.Д., Лакеев А.М.// Эффективность обработки информации в системах траекторных измерений.– М.: Министерство обороны СССР, 1968.
- Паслён В.В. Новое в истории развития методов обработки данных внешнетраекторных измерений / В.В. Паслён, К.И. Мотылев , М.В. Михайлов // Вісник Дніпропетровського університету — Днепропетровск, ДНУ – 2007, №9
- Михайлов М.В.
Оптимизация месторасположения измерительных средств /
М.В. Михайлов, К.И. Мотылев, В.В. Паслён //
IХ Міжнародна молодіжна науково – практична конференція
Людина і Космос
: Збірник тез – Дніпропетровськ: 2007. - Башков Е.А. Адаптивное нелинейное оптимальное сглаживание многопараметрических данных измерений / Е.А. Башков, В.В. Паслён // Университетские микроспутники – перспективы и реальность: международная научно – практическая конференция – Днепропетровск, 2006.
