Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Обзор исследований и разработок
- Выводы
- Список источников
Введение
Вопросам построения и уравнивания свободных геодезических сетей уделяется большое внимание. Они используются при решении задачи оценивания деформаций, при уравнивании фотограмметрических построений, в задачах оптимизации сетей. Как пример эффективного применения высотных сетей можно привести задачу анализа устойчивости реперов высотной основы.
Следует также отметить, что с позиции системного подхода свободные сети представляют собой более целостное построение, тогда как сети несвободные являются их частными случаями. Поэтому иногда целесообразно геодезические сети уравнивать как свободные, а затем превращать в несвободные, фиксируя любые исходные данные.
1. Актуальность темы
Как известно, создание инженерно-геодезических сетей отличается рядом особенностей, обусловленных тем, что их проектирование выполняется для конкретного объекта (часто на застроенной территории). В отличии от обще геодезических сетей инженерно-геодезические сети имеют сложную конфигурацию, характеризуются нарушением геометрических требований, предъявляемых к геодезическим сетям. Кроме того точность в инженерно-геодезических сетях, предусматривающих вынос в натуру отдельных элементов конструкций, повышается по мере детализации строящегося объекта. Все вышеперечисленные аспекты обуславливают необходимость широкого использования в инженерно-геодезической практике свободных геодезических сетей. Поэтому актуальным является исследование точности создания инженерно-геодезических сетей.
2. Цель и задачи исследования, планируемые результаты
Целью исследования является учет влияния выбора исходных данных на точность создания инженерно-геодезических сетей.
Основные задачи исследования:
- Установить особенности уравнивания свободных геодезических сетей.
- Выявить влияние выбора исходных данных на точность создания геодезического обоснования строительства инженерных сооружений.
Объект исследования: Инженерно-геодезические сети.
Предмет исследования: Методика выбора исходных данных, необходимых для уравнивания инженерно-геодезических сетей.
В рамках магистерской работы планируется получение актуальных научных результатов по следующим направлениям:
- Анализ способов уравнивания инженерно-геодезических сетей и определение оптимального.
- Определение оптимальных способов фиксации исходных данных в инженерно-геодезических сетях.
- Установление учета влияния исходных данных на создание инженерно-геодезических сетей.
3. Обзор исследований и разработок
В настоящее время уделяется все большее внимание вопросам уравнивания свободных геодезических сетей.
В первую очередь поясним, что мы будем понимать под свободной геодезической сетью в контексте данной работы.
Свободная геодезическая сеть – это геодезическое построение, в котором число исходных величин недостаточно для ориентации, масштабирования и фиксации сети в соответствующем пространстве.
Недостаток исходных величин в свободных геодезических сетях, а следовательно ненулевой дефект матрицы системы нормальных уравнений приводит к некоторому изменению методики уравнивания данного вида сетей.
Вопросу уравнивания свободных геодезических сетей уделили внимания в своих публикациях такие ученые как: Матвеев С.И., Ганьшин В.Н., Маркузе Ю.И., Андоленко В.И., Князев А.Г., Большаков В.Д. Рассмотрим основные положения, описанные в их работах.
Основным преимуществом свободных построений является независимость от ошибок исходных данных, что позволяет в полной мере оценить качество измерений [9].
В источнике [9] представлена следующая классификация свободных сетей в зависимости от значения дефекта матрицы нормальных уравнений (d):
- Максимально свободные сети -
 ;
;
- Полусвободные -
 ;
;
- Нуль-свободные -
 .
.
Дефектом матрицы  называется разность между наименьшим из чисел n и k и рангом матрицы.
называется разность между наименьшим из чисел n и k и рангом матрицы.
Рангом матрицы  называется максимальное число линейно независимых строк (столбцов). Иными словами наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается
называется максимальное число линейно независимых строк (столбцов). Иными словами наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается  . Очевидно, что значение ранга матрицы находится в диапазоне
. Очевидно, что значение ранга матрицы находится в диапазоне  , где min(n,k) - наименьшее из чисел n и k.
, где min(n,k) - наименьшее из чисел n и k.
Наиболее широкое применение в практике геодезического обеспечения строительства получили нуль-свободные построения, что обусловлено следующим:
- Нуль-свободные сети целесообразно применять для локальных построений, которые и используются при строительстве большинства инженерных сооружений.
- Так как при нуль-свободных построениях
 , то фиксация необходимых неизвестных не искажает геометрию сети, т.е. их применение не приводит, пользуясь термином строительной механики, к напряженной системе, что имеет место при традиционных геодезических построениях в виде несвободных сетей.
, то фиксация необходимых неизвестных не искажает геометрию сети, т.е. их применение не приводит, пользуясь термином строительной механики, к напряженной системе, что имеет место при традиционных геодезических построениях в виде несвободных сетей.
- В результате уравнивания сети как нуль-свободной получают координаты в требуемой системе, например, в системе координат главных осей сооружения [9].
Рассмотрим основные аспекты уравнивания свободных геодезических сетей.
Уравнивание свободных геодезических построений параметрическим способом приводит к возникновению параметрических уравнений связи параметров х с функцией измерений l, которое составляется для каждого измерения.
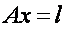
Матрица коэффициентов параметрических уравнений поправок А имеет дефект d (для нивелирных сетей d=1, для плановых сетей d=4, для пространственных - d=7). Вследствие этого матрица коэффициентов нормальных уравнений  является вырожденной и решения нормального уравнения
является вырожденной и решения нормального уравнения
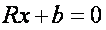
Находят по формуле:
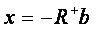
Где х – вектор искомых неизвестных;
 - псевдообратная матрица;
- псевдообратная матрица;

Как мы видим решение выполняется с использованием псевдообратной матрицы  , которая удовлетворяет свойствам:
, которая удовлетворяет свойствам:

Эти свойства констатируют симметрию взаимных произведений матриц А  . А также говорят о том что матрицы A
. А также говорят о том что матрицы A и
и  А являются эрмитовыми.
А являются эрмитовыми.
Основные вычислительные трудности при уравнивании свободных сетей связаны с определение псевдообратной матрицы  .
.
Существует много способов нахождения псевдообратной матрицы, перечислим только некоторые из них:
- Метод поэлементного вычисления матрицы
 .
.
- Метод окаймления.
- Метод, основанный на спектральном разложении матрицы R.
- Метод Гревиля.
Выбор исходных данных в инженерно-геодезических сетях различной конфигурации также оказывает существенное влияние на точность таких сетей. Задав оптимальное расположение исходных данных можно повлиять на распределение ошибок в сети, т.е. значительно повысить точность уравнивания.
Рассмотрим особенности выбора исходных данных в нуль-свободных плановых сетях. Данные сети предусматривают фиксацию трех параметров, необходимых для угловых и линейно-угловых построений. Существует два способа фиксации исходных параметров.
В качестве исходных данных принимаются:
- координаты любой точки сети и дирекционный угол какого-либо направления с нее;
- координата какой-либо точки сети и одна из координат любой другой точки сети.
В обоих случаях задается ориентация исходного направления относительно принятой системы координат, остающаяся после уравнивания неизменной.
В первом случае это можно выразить при помощи зависимостей:

Где  - координаты исходной точки сети;
- координаты исходной точки сети;
 - приращение координат исходной стороны;
- приращение координат исходной стороны;
 - уравненные значения указанных величин.
- уравненные значения указанных величин.
Недостатком данного способа выбора исходных данных является необходимость формировать дополнительное уравнение поправок:

Второй способ свободен от данного недостатка. В нем применяется традиционный прием вычеркивания столбца матрицы уравнений поправок, соответствующего фиксируемому элементу. При этом структура матрицы уравнений поправок остается неизменной.
В результате выполнения магистерской работы будет решена следующая научная задача: выявление изменения точности параметров, которые определяются в инженерно-геодезических сетях в зависимости от точности (ошибок) исходных данных и расположения исходных данных в сети.
В магистерской работе обработка инженерно-геодезических сетей выполняется с использованием программного комплекса МГСети.
Программа МГСети позволяет выполнять уравнивание планово-высотных, линейно-угловых сетей любой конфигурации, в том числе и свободных сетей.
Существенным преимуществом данного программного комплекса, качественно отличающим его от многих аналогичных программ, является то, что он позволяет в явной форме видеть распределение поправок между пунктами сети.
Уравнивание инженерно-геодезических сетей в данной работе выполняется в несколько этапов:
- Изначально сеть уравнивается как свободная, при этом фиксируются координаты любого пункта сети и дирекционный угол какого либо направления с него.
- Далее, опираясь на результаты свободного уравнивания, будет выполняться повторное уравнивание с фиксацией различных исходных данных в геодезической сети, что позволит выбрать оптимальный вариант уравнивания в зависимости от решаемой задачи.
Использование такого подхода к уравниванию инженерно-геодезических сетей позволяет исключить ошибки исходных данных и принимать во внимание только ошибки измерений. Это необходимо для того чтобы в полной мере оценить качество измерений инженерно-геодезических сетей.
Так как при решении большинства инженерных задач существенное значение имеют не только абсолютные величины ошибок но и их направление относительно сторон сети. Это вызвано тем, что при строительстве многих сооружений стремятся к достижению минимально-возможных ошибок по «ответственному» направлению. С целью наглядного отображения направления распространения ошибок, для каждого варианта уравнивания были построены эллипсы погрешностей (как показано на рисунке 1), которые позволяют выполнить анализ результатов уравнивания сетей и выбрать оптимальный вариант.
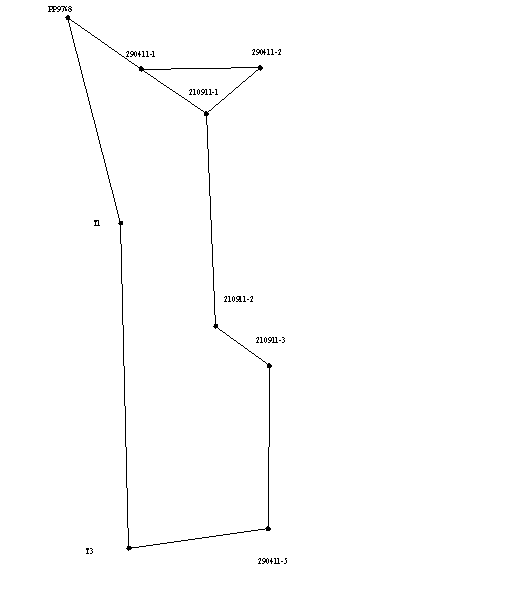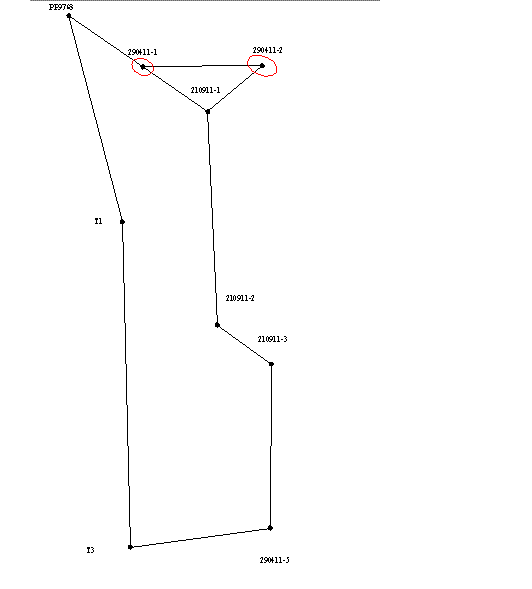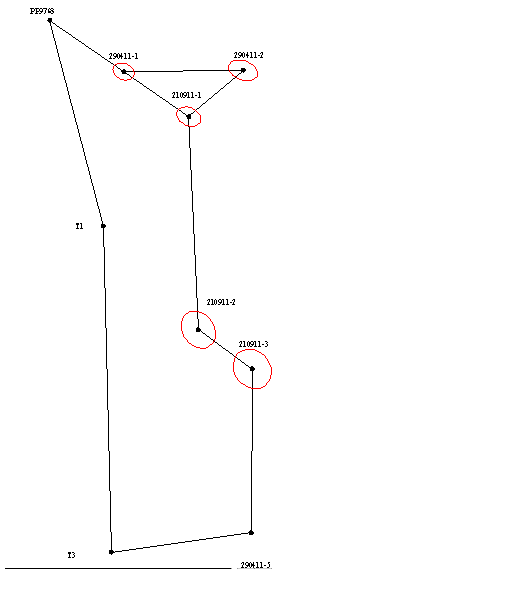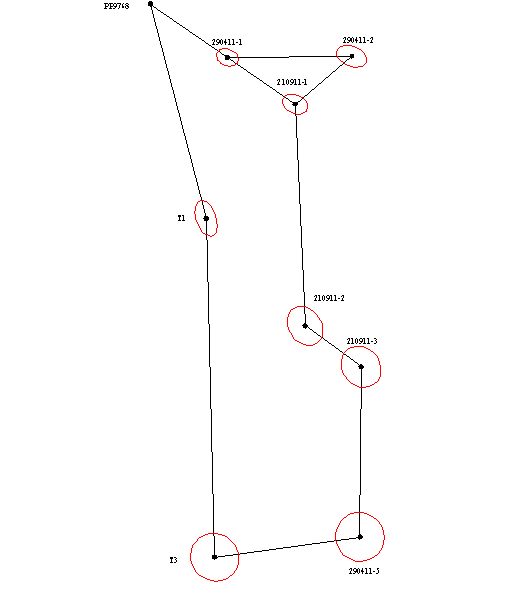
Рисунок 1 – Эллипсы погрешностей
Выводы
Теория уравнивания свободных геодезических сетей приобретает обобщенное значение, и становится понятным повышенный интерес к ней со стороны многих ученых. Естественно, что ряд вопросов свободного уравнивания каждый автор трактует по-своему, однако общее направление исследований состоит в объединении различных подходов к уравниванию.
Уравнивание свободных геодезических сетей имеет важное практическое значение, так как разбивочные сети строительной площадки должны обеспечивать высокую точность разбивочных построений и исключать ошибки исходных данных.
Выбор фиксации исходных данных в сетях различной конфигурации также оказывает существенное влияние на повышение точности результатов уравнивания, что немаловажно в современных условиях, когда возросли требования к точности геодезических построений, необходимых для геодезического обеспечения строительства инженерных сооружений.
Список источников
- http://www.dissland.com/ Швец С.В. Алгоритмы уравнивания свободных полигонометрических сетей с контролем грубых и систематических ошибок линейных измерений. Дисс. на соискание уч. степени канд. техн. наук: 25.00.32 М, 2005.
- Матвеев С.И. Единый подход к уравниванию свободных геодезических сетей.// Геодезия и картография.- 1985, вып. 7.- с. 6-11.
- Ганьшин В.Н. Анализ способов уравнивания свободных нивелирных сетей и оценка устойчивости реперов.// Геодезия и аэрофотосъемка. – 1979, вып. 3. – с. 5-12.
- Ганьшин В.Н., Стороженко А.Ф., Ильин А.Г. и др. Измерение вертикальных смещений сооружений и анализ устойчивости реперов. М., «Недра», 1981.
- Усов Д.В., Усова О.О., Ялтыхов В.В. Методика построения равноточных нуль-свободных нивелирных и спутниковых геодезических сетей.// Земля Беларуси.- 2009, вып. 1. – с. 38-40.
- Матвеев С.И. Программа уравнивания свободных нивелирных сетей.// Геодезия и фотограмметрия в горном деле. Свердловск. – 1978, вып. 5. – с. 39-42.
- Йовен И. Применение метода наименьших квадратов для уравнивания свободных сетей. // Геодезия, картография, землеустройство. Болгария. – 1980, вып. 20. – с. 14-17.
- Маркузе Ю.И. Взаимосвязь процедур уравнивания свободных и несвободных сетей. // Известия вузов. Геодезия и аэрофотосъемка. – 1984, вып. 3. – с. 3-14.
- Андоленко В.И. Исследование точности создания сетей специального назначения и разработка методов геодезического обеспечения строительства реакторных отделений АЭС. Дисс. на соискание уч. степени канд. техн. Наук. – М.: МИИГАиК. 1987.- 146 с.
- Князев А.Г. О способах вычисления псевдообратной матрицы при уравнивании свободных геодезических сетей. // Известия вузов. Геодезия и аэрофотосъемка. – 1984, вып. 5. – с. 25-34.
- Ганьшин В.Н. Псевдообращение матрицы нормальных уравнений свободных геодезических сетей. // Известия вузов. Геодезия и аэрофотосъемка. – 1989, вып. 6. – с. 3-5.
- http://book.tr200.net/v.php?id=628858 Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений: Учебное пособие для вузов.- М.:Недра, 1984, 352 с.
- http://www.twirpx.com/file/91607/ Теория матриц./Ланкастер П. – М.: Наука, 1982. – 272 с.
- http://www.nsu.ru/mmf/tvims/chernova/tv/portr.pdf Чернова Н.И. Теория вероятностей: Учеб. пособие/ Сиб-ГУТИ. Новосибирск, 2007. – 128с.
- http://www.mirknig.com/knigi/ Губанов В.С. Обобщенный метод наименьших квадратов. Теория и применение в астрометрии. – М.: Наука, 1997. – 319с.
- http://mirknig.com/knigi/ Чеботарев А.С. Способ наименьших квадратов. – М.: Геодезический факультет и военно-геодезическое отделение Московского межевого института, Издательство Московского высшего технического училища, 1928. – 475 с.
- Разумов О.С. О некоторых свойствах псевдообратной матрицы нормальных уравнений свободных геодезических сетей. – Изв. вузов. Геодезия и аэрофотосъемка, 1981, № 6, с. 3-7.
- Маркузе Ю.И., Хоанг Нгок Ха. Два способа получения псевдообратной матрицы при уравнивании свободных геодезических сетей с применением рекуррентной формулы. – Изв. вузов. Геодезия и аэрофотосъемка, 1985, № 1, с. 14-23.
