Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження та заплановані результати
- 3. Огляд досліджень та розробок
- Висновки
- Перелік посилань
Вступ
Питанням побудови і врівноваження вільних геодезичних мереж приділяється велика увага. Вони використовуються при вирішенні задачі оцінювання деформацій, при врівноваженні фотограмметричних побудов, в задачах оптимізації мереж. Як приклад ефективного застосування висотних мереж можна привести завдання аналізу стійкості реперів висотної основи.
Слід також зазначити, що з позиції системного підходу вільні мережі являють собою більш цілісне побудова, тоді як мережі невільні є їх окремими випадками. Тому іноді доцільно геодезичні мережі врівноважувати як вільні, а потім перетворювати на невільні, фіксуючи будь-які вихідні дані.
1. Актуальність теми
Як відомо, створення інженерно-геодезичних мереж відрізняється рядом особливостей, зумовлених тим, що їх проектування виконується для конкретного об'єкта (часто на забудованій території). На відміну від загально геодезичних мереж інженерно-геодезичні мережі мають складну конфігурацію, яка характеризується порушенням геометричних вимог, що пред'являються до геодезичним мереж. Крім того точність в інженерно-геодезичних мережах, які передбачають винесення в натуру окремих елементів конструкцій, підвищується в міру деталізації об'єкту, що будується. Всі перераховані вище аспекти обумовлюють необхідність широкого використання в інженерно-геодезичній практиці вільних геодезичних мереж. Тому актуальним є дослідження точності створення інженерно-геодезичних мереж.
2. Мета і задачі дослідження та заплановані результати
Метою дослідження є врахуваня впливу вихідних даних на точність створення інженерно-геодезичних мереж.
Основні задачі дослідження:
- Встановити особливості врівноваження вільних мереж.
- Виявити вплив вибору вихідних даних на точність створення геодезичного обгрунтування будівництва інженерних споруд.
Об'єкт дослідження:Інженерно-геодезичні мережі.
Предмет дослідження:Методика вибору вихідних даних, необхідних для врівноваження інденерно-геодезичних мереж.
В рамках магістерської роботи планується отримання актуальних наукових результатів по наступним напрямкам:
- Аналіз способів врівноваження інженерно-геодезичних мереж і визначення оптимального.
- Визначення оптимальних способів фіксації вихідних даних в інженерно-геодезичних мережах.
- Встановлення врахування впливу вихідних даних на створення інженерно-геодезичних мереж.
3. Огляд досліджень та розробок
В даний час приділяється все більша увага питанням врівноваження вільних геодезичних мереж.
У першу чергу пояснимо, що ми будемо розуміти під вільною геодезичної мережею в контексті даної роботи.
Вільна геодезична мережа - це геодезична побудова, в якій число вихідних величин недостатньо для орієнтації, масштабування і фіксації мережі у відповідному просторі.
Брак вихідних величин у вільних геодезичних мережах, а отже ненульовий дефект матриці системи нормальних рівнянь призводить до деякої зміни методики врівноваження даного виду мереж.
Питанню врівноваження вільних геодезичних мереж приділили увагу в своїх публікаціях такі вчені як: Матвєєв С.І., Ганьшин В.М., Маркузе Ю.І., Андоленко В.І., Князєв А.Г., Большаков В.Д. Розглянемо основні положення, описані в їх роботах.
Основною перевагою вільних побудов є незалежність від помилок вихідних даних, що дозволяє повною мірою оцінити якість вимірювань [9].
У джерелі [9] представлена наступна класифікація вільних мереж в залежності від значення дефекту матриці нормальних рівнянь (d):
- Максимально вільні мережі -
 ;
;
- Напіввільні -
 ;
;
- Нуль-вільні -
 .
.
Дефектом матриці  називається різниця між найменшим з чисел n і k і рангом матриці.
називається різниця між найменшим з чисел n і k і рангом матриці.
Рангом матриці  називається максимальне число лінійно незалежних строк (стовпців). Іншими словами найбільший з порядків мінорів даної матриці, відмінних від нуля, називається рангом матриці. Позначається
називається максимальне число лінійно незалежних строк (стовпців). Іншими словами найбільший з порядків мінорів даної матриці, відмінних від нуля, називається рангом матриці. Позначається  . Очевидно, що значення рангу матриці знаходиться в діапазоні
. Очевидно, що значення рангу матриці знаходиться в діапазоні  , де min(n,k) - наименше з чисел n і k.
, де min(n,k) - наименше з чисел n і k.
Найбільш широке застосування в практиці геодезичного забезпечення будівництва отримали нуль-вільні побудови, що обумовлено наступним:
- Нуль-вільні мережі доцільно застосовувати для локальних побудов, які і використовуються при будівництві більшості інженерних споруд.
- Так як при нуль-вільних побудовах
 , то фіксація необхідних невідомих не спотворює геометрію мережі, тобто їх застосування не призводить, користуючись терміном будівельної механіки, до напруженої системи, що має місце при традиційних геодезичних побудовах у вигляді невільних мереж.
, то фіксація необхідних невідомих не спотворює геометрію мережі, тобто їх застосування не призводить, користуючись терміном будівельної механіки, до напруженої системи, що має місце при традиційних геодезичних побудовах у вигляді невільних мереж.
- В результаті врівноваження мережі як нуль-вільної отримують координати в необхідній системі, наприклад, в системі координат головних осей споруди [9].
Розглянемо основні аспекти врівноваження вільних геодезичних мереж.
Врівноваження вільних геодезичних побудов параметричним способом призводить до виникнення параметричних рівнянь зв'язку параметрів х з функцією вимірювань l, які складаються для кожного вимірювання.
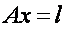
Матриця коефіцієнтів параметричних рівнянь поправок А має дефект d (для нівелірних мереж d = 1, для планових мереж d = 4, для просторових - d = 7). Внаслідок цього матриця коефіцієнтів нормальних рівнянь  є виродженою і рішення нормального рівняння
є виродженою і рішення нормального рівняння
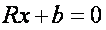
Знаходять за формулою:
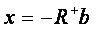
Де х - вектор шуканих невідомих;
 - псевдообернена матриця;
- псевдообернена матриця;
 .
.
Як ми бачимо рішення виконується з використанням псевдооберненої матриці  , яка задовольняє властивостям:
, яка задовольняє властивостям:

Ці властивості констатують взаїмну симетрію матриці А та  . А також кажуть про те, що матриці A
. А також кажуть про те, що матриці A і
і  А є ермітовими.
А є ермітовими.
Основні обчислювальні труднощі при зрівнюванні вільних мереж пов'язані з визначення псевдообернених матриці  .
.
Існує багато способів знаходження псевдооберненої матриці, перерахуємо лише деякі з них:
- Метод поелементного обчислення матриці
 .
.
- Метод облямівки.
- Метод, заснований на спектральному розкладанні матриці R.
- Метод Гревіля.
Вибір вихідних даних в інженерно-геодезичних мережах різної конфігурації також суттєво впливає на точність таких мереж. Задавши оптимальне розташування вихідних даних можна вплинути на розподіл помилок у мережі, тобто значно підвищити точність врівноваження.
Розглянемо особливості вибору вихідних даних в нуль-вільних планових мережах. Дані мережі передбачають фіксацію трьох параметрів, необхідних для кутових та лінійно-кутових побудов. Існує два способи фіксації вихідних параметрів.
В якості вихідних даних приймаються:
- координати будь-якої точки мережі і дирекційний кут будь-якого напряму з неї;
- координата будь-якої точки мережі і одна з координат будь-якої іншої точки мережі.
В обох випадках задається орієнтація вихідного напрями щодо прийнятої системи координат, що залишається після врівноваження незмінною.
У першому випадку це можна виразити за допомогою залежностей:

Де  - координати вихідної точки мережі;
- координати вихідної точки мережі;
 - приріст координат вихідної сторони;
- приріст координат вихідної сторони;
 - врівноважені значення зазначених величин.
- врівноважені значення зазначених величин.
Недоліком даного способу вибору вихідних даних є необхідність формувати додаткове рівняння поправок:

Другий спосіб вільний від даного недоліку. У ньому застосовується традиційний прийом викреслювання стовпця матриці рівнянь поправок, відповідного зафіксованому елементу. При цьому структура матриці рівнянь поправок залишається незмінною.
В результаті виконання магістерської роботи буде вирішена наступна наукова задача: виявлення зміни точності параметрів, які визначаються в інженерно-геодезичних мережах в залежності від точності (помилок) вихідних даних і розташування вихідних даних в мережі.
У магістерській роботі обробка інженерно-геодезичних мереж виконується з використанням програмного комплексу МГСети.
Програма МГСети дозволяє виконувати врівноваження планово-висотних, лінійно-кутових мереж будь-якої конфігурації, в тому числі і вільних мереж.
Істотною перевагою даного програмного комплексу, що якісно відрізняє його від багатьох аналогічних програм, є те, що він дозволяє в явній формі бачити розподіл поправок між пунктами мережі.
Врівноваження інженерно-геодезичних мереж в даній роботі виконується в декілька етапів:
- Спочатку мережа зрівнюється як вільна, при цьому фіксуються координати будь-якого пункту мережі і дирекційний кут якого або напряму з нього.
- Далі, спираючись на результати вільного врівноваження, буде виконуватися повторне врівноваження з фіксацією різних вихідних даних в геодезичній мережі, що дозволить вибрати оптимальний варіант зрівнювання в залежності від розв'язуваної задачі.
Використання такого підходу до зрівнювання інженерно-геодезичних мереж дозволяє виключити помилки вихідних даних і приймати до уваги тільки помилки вимірювань. Це необхідно для того щоб повною мірою оцінити якість вимірювань інженерно-геодезичних мереж.
Так як при вирішенні більшості інженерних задач істотне значення мають не тільки абсолютні величини помилок але і їх напрям відносно сторін мережі. Це викликано тим, що при будівництві багатьох споруд прагнуть до досягнення мінімально-можливих помилок по «відповідальному» напрямку. З метою наочного відображення напрямку поширення помилок, для кожного варіанту зрівнювання були побудовані еліпси похибок (як показано на малюнку 1), які дозволяють виконати аналіз результатів зрівнювання мереж і вибрати оптимальний варіант.
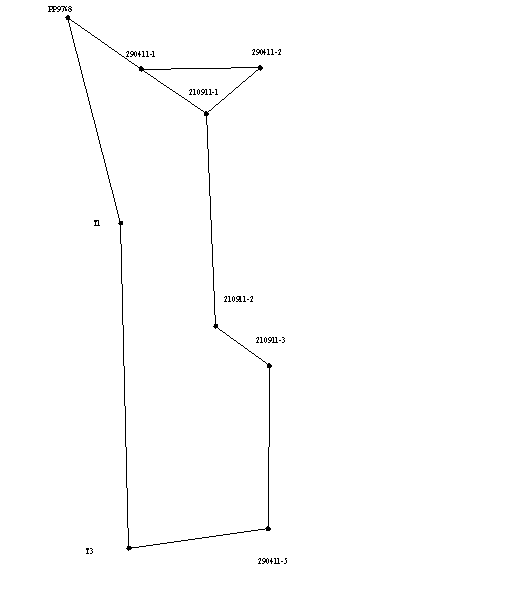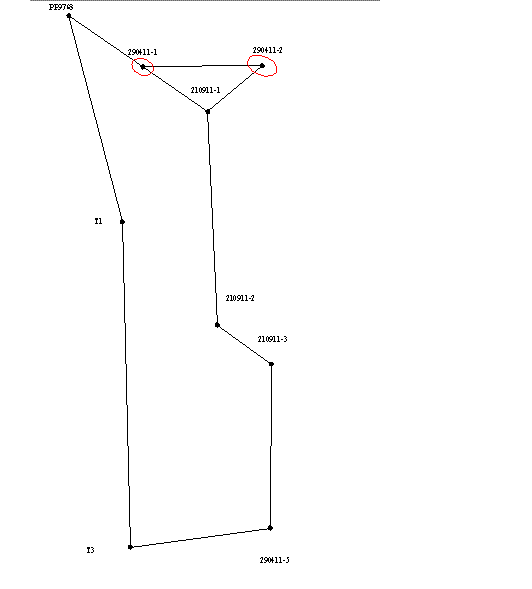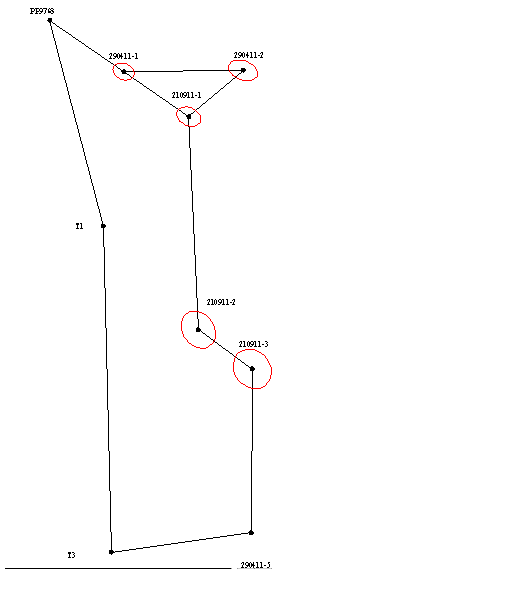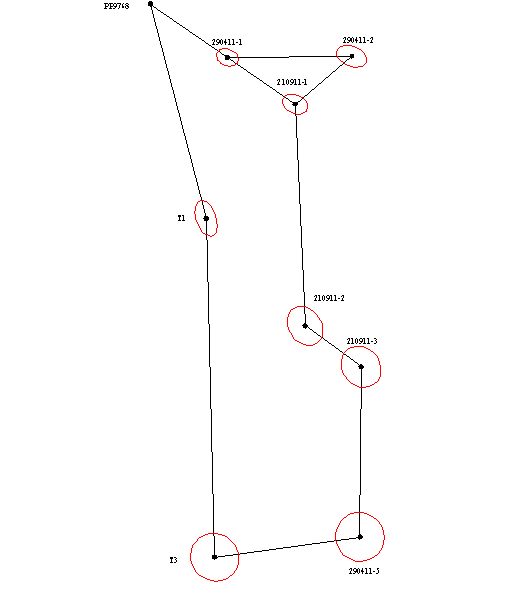
Малюнок 1 - Еліпси похибок.
Висновки
Теорія зрівнювання вільних геодезичних мереж набуває узагальнене значення, і стає зрозумілим підвищений інтерес до неї з боку багатьох учених. Природно, що ряд питань вільного зрівнювання кожен автор трактує по-своєму, проте загальний напрямок досліджень полягає в об'єднанні різних підходів до зрівнювання.
Врівноваження вільних геодезичних мереж має важливе практичне значення, так як розбивочні мережі будівельного майданчика повинні забезпечувати високу точність розбивочних побудов і виключати помилки вихідних даних.
Вибір фіксації вихідних даних в мережах різної конфігурації також істотно впливає на підвищення точності результатів врівноваження, що важливо в сучасних умовах, коли зросли вимоги до точності геодезичних побудов, необхідних для геодезичного забезпечення будівництва інженерних споруд.
Перелік посилань
Список источников
- http://www.dissland.com/ Швец С.В. Алгоритмы уравнивания свободных полигонометрических сетей с контролем грубых и систематических ошибок линейных измерений. Дисс. на соискание уч. степени канд. техн. наук: 25.00.32 М, 2005.
- Матвеев С.И. Единый подход к уравниванию свободных геодезических сетей.// Геодезия и картография.- 1985, вып. 7.- с. 6-11.
- Ганьшин В.Н. Анализ способов уравнивания свободных нивелирных сетей и оценка устойчивости реперов.// Геодезия и аэрофотосъемка. – 1979, вып. 3. – с. 5-12.
- Ганьшин В.Н., Стороженко А.Ф., Ильин А.Г. и др. Измерение вертикальных смещений сооружений и анализ устойчивости реперов. М., «Недра», 1981.
- Усов Д.В., Усова О.О., Ялтыхов В.В. Методика построения равноточных нуль-свободных нивелирных и спутниковых геодезических сетей.// Земля Беларуси.- 2009, вып. 1. – с. 38-40.
- Матвеев С.И. Программа уравнивания свободных нивелирных сетей.// Геодезия и фотограмметрия в горном деле. Свердловск. – 1978, вып. 5. – с. 39-42.
- Йовен И. Применение метода наименьших квадратов для уравнивания свободных сетей. // Геодезия, картография, землеустройство. Болгария. – 1980, вып. 20. – с. 14-17.
- Маркузе Ю.И. Взаимосвязь процедур уравнивания свободных и несвободных сетей. // Известия вузов. Геодезия и аэрофотосъемка. – 1984, вып. 3. – с. 3-14.
- Андоленко В.И. Исследование точности создания сетей специального назначения и разработка методов геодезического обеспечения строительства реакторных отделений АЭС. Дисс. на соискание уч. степени канд. техн. Наук. – М.: МИИГАиК. 1987.- 146 с.
- Князев А.Г. О способах вычисления псевдообратной матрицы при уравнивании свободных геодезических сетей. // Известия вузов. Геодезия и аэрофотосъемка. – 1984, вып. 5. – с. 25-34.
- Ганьшин В.Н. Псевдообращение матрицы нормальных уравнений свободных геодезических сетей. // Известия вузов. Геодезия и аэрофотосъемка. – 1989, вып. 6. – с. 3-5.
- http://book.tr200.net/v.php?id=628858 Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений: Учебное пособие для вузов.- М.:Недра, 1984, 352 с.
- http://www.twirpx.com/file/91607/ Теория матриц./Ланкастер П. – М.: Наука, 1982. – 272 с.
- http://www.nsu.ru/mmf/tvims/chernova/tv/portr.pdf Чернова Н.И. Теория вероятностей: Учеб. пособие/ Сиб-ГУТИ. Новосибирск, 2007. – 128с.
- http://www.mirknig.com/knigi/ Губанов В.С. Обобщенный метод наименьших квадратов. Теория и применение в астрометрии. – М.: Наука, 1997. – 319с.
- http://mirknig.com/knigi/ Чеботарев А.С. Способ наименьших квадратов. – М.: Геодезический факультет и военно-геодезическое отделение Московского межевого института, Издательство Московского высшего технического училища, 1928. – 475 с.
- Разумов О.С. О некоторых свойствах псевдообратной матрицы нормальных уравнений свободных геодезических сетей. – Изв. вузов. Геодезия и аэрофотосъемка, 1981, № 6, с. 3-7.
- Маркузе Ю.И., Хоанг Нгок Ха. Два способа получения псевдообратной матрицы при уравнивании свободных геодезических сетей с применением рекуррентной формулы. – Изв. вузов. Геодезия и аэрофотосъемка, 1985, № 1, с. 14-23.
