DonNTU   Masters' portal

Abstract on theme: "Analysis and development of algorithm for determining
the relative position of objects in images"


Table of contents

Introduction

Every human has two eyes that see the same picture, but slightly different angles. The difference in these observation angles allows the brain to calculate the depth of space, the relative position of objects, the distance to each object.

The human brain is very efficient searches for the matching image from the left and right eyes. Sometimes technical devices are needed for such abilities. How exactly images are matched in the brains of animals is unknown. Therefore, scientists from around the world doing research in an attempt to find a fast algorithm for quality images matching.

The result of matching the images will allow technology to "see" the location of the observed objects in three dimensions, to determine how close the object to the camera.

This information may be useful in various fields such as for entertainment purposes and to help people.

1. Relevance

The problem of matching images is to establish a correspondence between the points of two or more images. This problem is a fundamental problem of computer vision, since the need of combining images occur in the solution of such tasks as identifying changes in a series of images, motion analysis, combining information from different sensors, stereo vision and texture analysis. Similar problems, in turn, arise in biomedical applications, robotic vision, remote data collection, so the practical usefulness of the automatic alignment of images is undeniable.

Problem of matching images is solved only for some special cases, and is still relevant. Basic research directed at building a reliable automated systems that do not require human intervention. These systems represent a large practical interest and are often used in a variety of techniques, but at present these systems are designed only for a narrow class of problems.

For example, a robot equipped with such vision can effectively navigate in environment, get the distance to various objects, produce better segmentation and object recognition, build three-dimensional models of buildings, rooms in which they were, etc.

Such technologies may even save lives. Getting information about the third dimension would allow vehicles to determine the distance to nearby vehicles, signspillars, pedestrians, which in turn will be needed for emergency braking, bypass the object on the path of the vehicle, sign recognition and displays the recommendations of the driver.

2. Aims and Objectives

The aim of this work is to review existing approaches of solving matching images problem, obtaining data about the spatial arrangement objects, collect data needed to develop a new algorithm that allows for a relatively short period of time calculate acceptable quality disparity map.

The object of study is the process of identifying correspondences in stereo images.

Scope of the work – the existing algorithms that find correspondence in the images.

The main tasks are to: review existing algorithms of image matching, review algorithms of disparity map calculation, study the stereo images properties, design modification of disparity map calculation algorithm.

3. Research & Development Overview

Researches on comparison of images in Ukraine and CIS countries are poorly developed, but the topic is well revealed by numerous publications of foreign scientists.

In [1] proposed an algorithm for estimating the accuracy of matching to obtain information on the adequacy of comparison, in [2] discusses algorithms for matching three-dimensional reconstruction. For the purpose of preliminary comparison of images you can use the algorithm for coarse alignment of the found lines [3].

The three-dimensional reconstruction requires a comparison with high accuracy, in [4,5] proposed a method refinement of three-dimensional model obtained by a small number of characteristic points.

From the local works can be noted the work Agarkov A.B. from the Institute of Artificial Intelligence [6,7], which proposed a method of representing images in the form of graphs, image matching is based on a comparison of this graphs.
All the essential information has been obtained it from the English-language sources.

Efficient search for matches on the small images after reduction with aliasing is described in [8]. In [9] the fast correlation algorithm has described. In [10,11] images are matched by silhouettes, contours. In [12] proposed improved  real time correlation algorithm. Correlation algorithm with taking into account the color information is in [13]. Algorithm in [14] is based on energy minimization of the global functions with discontinuities, in [15] used the method of cuts in graphs, in [16] used information of the image segments.

To find the key points of the images are frequently used SIFT [17], SURF [18] algorithms. A good method of inexact matching of similar sequences is a dynamic programming [19].

4. Image matching algorithms


4.1 The input data and results

In this work as input data will be two stereo images. In general, there may be several. These images are obtained by photographing the same scene but with a slight offset, a slightly different angle.

Figure 4.1 shows two rectified stereo images.

Рисунок 4.1 – Ректифицированные стереоизображения

Figure 4.1 – Rectified stereo images

The above images are rectified, it means that the images are oriented at equal angles and have the same scale. For clarity in figure 4.2 presented not rectified images.

Рисунок 4.2 – Не ректифицированные стереоизображения

Figure 4.2 – Not rectified stereo images

The task of the algorithm is to find a displacement of the points left (right) images to coincide with the corresponding points of the right (left) images.

Solution is two-dimensional array of numbers. It can be conveniently represented in graphical form, where the value of each element corresponds to the brightness of the pixel.

Such a graphical representation of the solutions is called disparity map, depth map, shifts map, inconsistencies map. Disparity map presented in Figure 4.3.

Рисунок 4.3 – Карта диспарантности стереоизображений

Figure 4.3 – Disparity map

4.2 Rectification of images

Before calculating the disparity map, you must rectify the images, rotate them in the same direction and bring to the same scale.

This is done by looking for key points in the images and then the points matched with each other.

The next step is calculating the affine transformation matrix and then the images can be easily rectificated.

One of the most popular methods of finding the key points are the methods of SIFT, SURF and Harris detector.

4.3 Disparity map calculation algorithms

Figure 4.4 shows the animation of manual matching of the two image rows. As seen in the animation, when some parts of the image are coinciding the others do not match. The task of matching is to match all parts of the image.

Рисунок 4.4 – Визуализация процесса ручного сопоставления строк изображения

Figure 4.4 – Animation of manual matching of the two image rows
(7 frames, first frame delay 2 sec, others – 1 sec, repetitions – 7, file size – 46,2 Kb)

Image matching is often based on the correlation approach and methods based on energy minimization.
Correlation algorithm compares each point of one image one line with each point of the other image in the same line. Two-dimensional array of correlation will be obtained as result of comparison of one line (Figure 4.5). In this array a lower value means the most probable solution. Searching for most probable solutions we construct a disparity map. For better results usually compare several neighbor pixels (e.g., window 8x8 pixels).

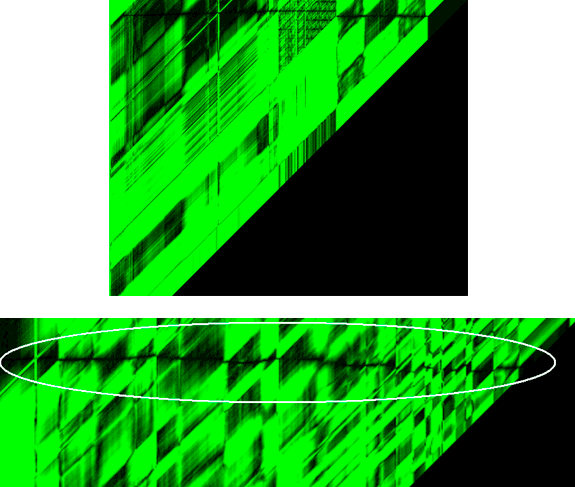
Рисунок 4.5 – Графическое представление результата сравнения строк

Figure 4.5 – Two-dimensional array of correlation

The dark line on this graph is the optimal solution of matching. The main task is to identify it properly, since in most cases it is difficult to identify.

There is a certain energy function in the methods based on minimization of energy, whose value depends on what pixels from one image associated with pixels from another image. This function should be minimized. It will be the solution of the matching. The quality of this approach is much higher than the correlation method, but such algorithms work much longer and much harder to implement.

Some algorithms are based on searching for specific details, areas, shapes, and then found objects matched.
Most algorithms are not used color images, and use black and white, but some use color information to obtain more accurate results. Some algorithms are used a Markov chain.

There are algorithms that represent the image as a graph, where nodes are the points of the image and the edges are links between the points. By defining the intersection of two graphs, you will receive the correspondence between the stereo image pixels.

Pretty simple and effective method is dynamic programming. The fastest algorithms are based on dynamic programming and the correlation approach.

5. Analyze of Dynamic programming algorithm and uniform regions

Dynamic Programming (DP) is used to compare two sequences of data, the result is a line sequences, which will coincide with the maximum amount of data. DP is often used for solving a fuzzy comparison of sequences, text strings, the comparison of DNA chains, audio sequences, as well as images.

DP algorithm is simple to implement and gives good results. Consider the algorithm in detail.

As the input data used two horizontal line of the left and right images. Let L (x, y), R (x, y) - the brightness of the point with coordinates (x, y) for left and right images, respectively.

The initial data for the DP is a correlation matrix Dif [i, j], which returns the difference of the pixel L (i, y), and pixel R (j, y). This matrix discussed earlier (Figure 4.5). Usually the comparison is made not by one pixel, but several neighbors, it refines the results and reduces the number of ambiguous solutions.

The next step is to calculate the dynamic programming matrix A [i, j]. At the beginning of the algorithm A [0,0] = 0. The calculation is performed for i = 1 .. n, j = 1 .. n, where n - the width of the image. The elements of this matrix are calculated as follows:


Minimum = Min( A[i-1,j], A[i,j-1], A[i-1,j-1] )

A[i,j] = Minimum + Dif[i,j].


Function Min (a, b, c) returns the minimum value of the argument. Matrix of differences (correlations) and the dynamic programming matrix presented in figure 5.1.

Рисунок 5.1 – Матрица разностей и матрица ДП с найденным путем

Figure 5.1 – Differences matrix and DP matrix with solution path

As seen in Figure 5.1, over the matrix of differences difficult to accurately identify the correct solution, but the DP matrix solution clearly stands out, you just go through this matrix and find the way. Algorithm for finding solution:


DisparityMapL [i,y] = j-i

DisparityMapR [j,y] = i-j

Up = A[i-1,j]

Left = A[i,j-1]

UpLeft = A[i-1,j-1]

Minimum = Min( Up,Left,UpLeft )

case Minimum of

UpLeft : i=i-1;j=j-1

Left : j=j-1

Up : i=i-1

end


At the beginning of the algorithm i = n and j = n. The above steps apply as long as i and j will be zero. (i, j) defines the position in the matrix DP. DisparityMapR[x, y] and DisparityMapL[x, y] is calculated disparity map for left and right images respectively (one map will be enough).

As can be seen from the description the algorithm is simple to implement, but at the same time is a good and high quality stereo correspondence search method.

Each row of images is treated independently from the rest. On the one hand it's good, since the algorithm can be divided into a large number of processors, thereby increasing the speed of computation. On the other hand, the lack of interconnection with neighboring lines causes the effect of the comb. This effect presented in Figure 5.2.

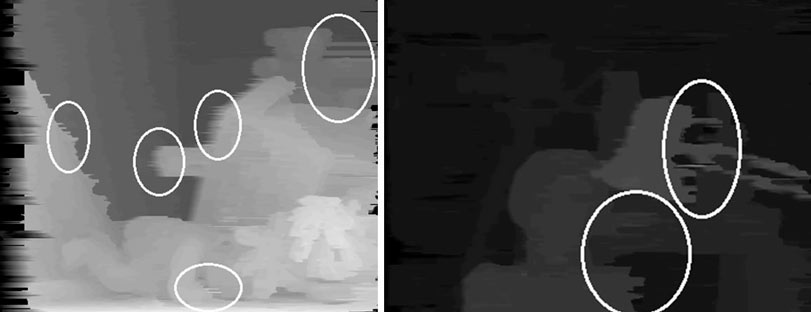
Рисунок 5.2 – Характерный для ДП эффект гребенки на карте диспарантности

Figure 5.2 – DP effect of the comb

These errors occur because the image contains homogeneous areas, for which the algorithm applies the same depth as the previous points. The essence of the algorithm DP is to do as little as possible transitions from one depth to another, so in some cases the depth remains unchanged where it is not necessary.

Algorithms that use search in the image of homogeneous areas better able to cope with such cases. These algorithms identify certain areas, certain objects and match them entirely. With this approach, the borders will be more clear and correct.

An example of such homogeneous areas can be areas identified in Figure 5.3.

Рисунок 5.3 – Пример однородных областей

Figure 5.3 – Example of homogeneous areas

Such areas can be identified by using a special algorithm, and then to make an exact match with the same areas on the other picture. This approach allows to find an exact match found in the image of objects, while maintaining the smooth object boundaries.

The disadvantage of this approach can be considered the focus on homogeneous areas. The algorithm is completely dependent on the presence of such regions, which in some images may be absent, and therefore, the algorithm will not work correctly.

By combining the two approaches, one can use the advantages of each method and eliminate shortcomings. Making the search for homogeneous regions and their comparison can facilitate and clarify the operation of the correlation algorithm. Such an approach would clarify the work of the DP algorithm [20].

Conclusion

Image matching is required in many spheres of human activity: photogrammetry, robots vision, navigation systems, building autonomous vehicles, biomedical applications. Various authors have proposed a large number of solutions of the image matching. Modern algorithms have a common flaw – low performance  of high-quality algorithms. Therefore, there is a need to create fast and efficient algorithms.

As a result of the review and analysis of existing algorithms of stereo images matching, the main approaches have been chosen to be used in the further development. In the studies have been analyzed the advantages and disadvantages of existing algorithms, features of stereo images and the typical errors of calculations that will be taken into account in the further development of the algorithm. Further studies are aimed at developing a method of identification and selection of homogeneous areas, the optimization calculations, the acceleration of the algorithm by using the already calculated data.


At the time of writing the abstract, master's work is not yet complete. The finished version of the work may be obtained from the author or his supervisor after December 20, 2012.


References

  1. Гришин В. А Оценка точности установления соответствия // Доклады 10-ой Международной конференции и выставки "Цифровая обработка сигналов и ее применение", 26-28 марта 2008 года. Серия: Цифровая обработка сигналов и ее применение. Выпуск: Х-2. С. 428-431.
  2. Юрин Д. В. , Крылов А. С. , Волегов Д. Б. , Насонов А . В. , Свешникова Н. В. Методы и алгоритмы совмещения изображений и их применение в задачах восстановления трехмерных сцен и панорам, анализе медицинских изображений, Москва, В МиК МГУ
  3. Волегов Д.Б. , Юрин Д.В. Грубое совмещение изображений по найденным на них прямым линиям // Труды конференции Графикон 2006, Новосибирск., с . 463–466. http://www.graphicon.ru
  4. Свешникова Н.В. Уточнение сеточной модели трехмерной сцены, предварительно восстановленной по малому количеству характеристических точек // Труды конференции Графикон 2007, Москва 2007, http://www.graphicon.ru
  5. Свешникова Н.В. , Юрин Д.В. Алгоритмы факторизации: достоверность результата и применение для восстановления эпиполярной геометрии // Труды конференции Графикон 2006, Новосибирск., с. 158–165.
  6. А.В. Агарков Построение карты диспаратности на основе сравнения графов, Институт проблем искусственного интеллекта, г. Донецк, Украина , 2006
  7. А.В. Агарков Иерархическое представление изображения  с помощью графа, Институт проблем искусственного интеллекта, г. Донецк, Украина, 2003
  8. Henkel R.D. Fast Stereovision by Coherence Detection / Ed. by G. Sommer, K. Daniilidis, J. Pauli // Proc. of the 7th International Conf. on Computer Analysis of Images and Patterns, CAIP'97 in Kiel, LNCS 1296, Springer. – Berlin. – 1997. – P. 297-304.
  9. Stefano L.D., Marchionni M., Mattoccia S., Neri G. A Fast Area-Based Stereo Matcting Algorithm //  Proc. of 15th International Conf. on Vision Interface. – 2002. – P. 146-153.
  10. Egnal G., Mintz M., Daniilidis K. Limiting the Search Rang of Correlation Stereo Using Silhouettes // Proc. of 15th International Conf. on Vision Interface. – 2002. – P. 170-177.
  11. Boufama B., Jin K. Towards a Fast and Reliable Dense Matcing Algorithm // Proc. of 15th International Conf. on Vision Interface. – 2002. – P. 178-185.
  12. Hirschmuller H. Improvements in Real-Time Correlation-Based Stereo Vision // CVPR 2001 Stereo Workshop / IJCV. – 2002.
  13. Muhlmann K., Maier D., Hesser J., Manner R. Calculating Dense Disparity Maps from Color Stereo Images, an Efficient Implementation // CVPR 2001 Stereo Workshop / IJCV 2002.
  14. Boykov Yu., Veksler O., Zabih R. A New Algorithm for Energy Minimization with Discontinuities // EMMCVPR. – 1999. – P. 205-220.
  15. Kolmogorov V., Zabih R. Computing Visual Correspondence with Occlusions via Graph Cuts  // ICCV. – 2001. – P. 508-515.
  16. Kawai Y., Ueshiba T., Ishiyama Y., Sumi Y., Tomita F. Stereo Correspondence Using Segment Connectivity // Proc. 14th International Conf. on Pattern Recognition, ICPR'98.  – Brisbane (Australia). – 1998. – P. 648-651.
  17. Построение SIFT дескрипторов и задача сопоставления изображений [электронный ресурс]. – Режим доступа: http://habrahabr.ru/post/106302/
  18. Обнаружение устойчивых признаков изображения: метод SURF [электронный ресурс]. – Режим доступа: http://habrahabr.ru/post/103107/
  19. Динамическое программирование [электронный ресурс]. – Режим доступа: http://rain.ifmo.ru/cat/view.php/...
  20. Чигарев И.А. Разработка алгоритма сопоставления стереоизображений и построения карты диспарантности // Современная информационная Украина: информатика, экономика, философия / Материалы VI Международной научно-практической конференции молодых ученых, аспирантов, студентов. - Донецк, ДонНТУ - 2012.