ДонНТУ   Портал магістрів

Реферат за темою: “Аналіз та розробка алгоритму визначення взаємного
розташування об’єктів на зображеннях”


Содержание

Вступ

Кожна людина має два ока, які бачать одну й ту ж картинку, але трохи під різними кутами. Різниця в цих кутах дозволяє мозку обчислити глибину навколишнього людини простору, взаємне розташування об’єктів, відстань до кожного з об’єктів.

Людський мозок, як і мозок багатьох інших тварин з бінокулярним зором, дуже ефективно справляється із завданням пошуку відповідностей зображень, отриманих з лівого і правого очей. Але такі здібності іноді потрібні від техніки. Як саме відбувається співставлення зображень в мозку тварин невідомо, тому вчені різних країн займаються дослідженням даної теми намагаючись знайти оптимальний алгоритм якісного і швидкого співставлення зображень.

Результат співставлення зображень надасть можливість техніці “бачити” розташування спостережуваних об’єктів в трьох вимірах, тобто можна буде визначити, який об’єкт знаходиться близько, а який дуже далеко від камери. Дана інформація може бути корисною в різних областях, як в розважальних цілях, так і з метою допомоги людині.

1. Актуальність теми

Проблема поєднання зображень полягає у встановленні відповідності між точками двох або більше зображень. Дана проблема є фундаментальною проблемою комп’ютерного бачення, оскільки необхідність поєднання зображень виникає при вирішенні таких завдань, як виявлення змін в серії зображень, аналіз руху, поєднання інформації від різних сенсорів, стереозір і текстурний аналіз. Подібні проблеми, в свою чергу, виникають в біомедичних застосуваннях, при вирішенні задач фотограмметрії і в зорі роботів, при дистанційному зборі даних, тому практична корисність автоматичного суміщення зображень безсумнівна.

Незважаючи на постійно виникаючу необхідність поєднання зображень, ця проблема вирішена тільки для деяких окремих випадків і до цих пір залишається актуальною. З одного боку, основні зусилля дослідників спрямовані на побудову стійких автоматичних систем, які не вимагають втручання людини. Ці системи являють собою величезний практичний інтерес і часто використовуються в різній техніці, але на даний момент такі системи розроблені лише для вузького класу задач. З іншого боку, виробляються спроби побудови інтелектуальних систем, які будуть самостійно аналізувати зображення, інтерпретувати, моделювати систему зорового сприйняття людини.

Наприклад, роботи з таким зором, можуть ефективніше орієнтуватися в просторі, отримувати більш повну картину навколишнього середовища, отримувати відстань до різних об’єктів, ефективніше проводити сегментацію і розпізнавання об’єктів, будувати тривимірну модель будівель, приміщень в яких вони були і т.д.

Такі технології можуть навіть рятувати життя людей. Отримання інформації про третій вимірі дозволить автомобілям визначати відстань до сусідніх автомобілів, знаків, стовпів, пішоходів, що в свою чергу знадобиться для екстреного гальмування, об’їзду об’єкта на шляху руху автомобіля, розпізнавання знаків і виведення рекомендацій водієві.

2. Мета і задачі дослідження та заплановані результати

Мета даної роботи полягає в огляді існуючих підходів у вирішенні завдання суміщення зображень та отриманні даних про просторове розташування об’єктів, а також в зборі даних, необхідних для розробки нового алгоритму, що дозволяє за відносно короткий проміжок часу отримати карту діспарантності прийнятної якості.

Об’єктом дослідження є процес виявлення відповідностей на зображеннях стереопари.

Предмет роботи - існуючі алгоритми виявлення відповідностей на зображеннях стереопари.

Основними завданнями є: огляд існуючих алгоритмів визначення взаємного розташування об’єктів на зображеннях, виявлення однакових об’єктів на зображеннях стереопари, побудови карти глибин сцени, вивчення властивостей стереозображень, розробка модифікації алгоритму побудови карти глибин.

3. Огляд досліджень і розробок

Дослідження в цій галузі в Україні та країнах СНД слабо розвинені, але дана тема добре розкривається численними публікаціями зарубіжних вчених.

В роботі [1] пропонується алгоритм оцінки точності зробленого суміщення для отримання інформації про адекватність співставлення зображень, а в [2] розглядаються самі алгоритми суміщення в задачах тривимірної реконструкції. З метою попереднього співставлення можна скористатися алгоритмом грубого суміщення по знайденим лініях [3].

Для тривимірної реконструкції необхідні результати співставлення з великою точністю, в роботі [4,5] пропонується метод уточнення тривимірної моделі, отриманої по невеликій кількості характерних точок.

З локальних робіт можна відзначити роботи Агаркова А.В. з Інституту проблем штучного інтелекту [6,7], в яких пропонується метод представлення зображень у вигляді графів та пошук відповідностей зображень заснований на порівнянні отриманих графів.

Численні публікації на тему співставлення стереозображень можна знайти на англійській мові. Більшість інформації було отримано саме з англомовних джерел.

Ефективний пошук відповідностей на маленьких зображеннях після зменшення без згладжування описаний в [8]. В [9] розглянуто швидкий кореляційний алгоритм. В [10,11] пропонується співставляти зображення по силуетам, контурам. В роботі [12] розглядається поліпшення кореляційного алгоритму працюючого в режимі реального часу. Ще один кореляційний алгоритм з урахуванням інформації про колір [13]. Є й інші не кореляційні алгоритми, наприклад, [14] заснований на мінімізації енергії глобальної функції з розривами, в [15] використовується метод розрізів на графах, в [16] для побудови карти діспарантності враховуються однорідності сегментів зображення.

Для знаходження ключових точок часто використовуються алгоритми SIFT [17], SURF [18]. Популярним методом неточного співставлення схожих послідовностей є динамічне програмування [19].

4. Підходи до вирішення задачі суміщення стереозображень


4.1 Вихідні дані і результати

Для розуміння теми співставлення стереозображень, визначимо, що є вхідними даними і що отримується в результаті роботи алгоритмів співставлення зображень.

В даній роботі в якості вхідних даних будуть розглядатися два стереозображення. У загальному випадку їх може бути декілька. Ці зображення отримуються шляхом фотографування однієї і тієї ж сцени, але з невеликим зміщенням, під трохи іншим кутом.

Наочним прикладом є зір людини. Очі людини трохи віддалені один від одного, але спрямовані в одну сторону, тобто очі бачать одну й ту ж картину. Такий зір називається бінокулярним. Завдяки тому, що очі отримують зображення одних предметів трохи з різних сторін, мозок, обробивши невідповідності зображень, дає людині відчуття об’єму, людина відчуває, які предмети знаходяться далеко, які близько.

На малюнку 4.1 зображено два ректифікованих стереозображення.

Рисунок 4.1 – Ректифицированные стереоизображения

Рисунок 4.1 – Ректифіковані стереозображення

Як видно з рисунку 4.1, зображення на перший погляд однакові, але насправді зображення отримані з різних позицій (наприклад, дах шпаківні на правому зображенні трохи ближче до синього фону).

Наведені вище зображення ректифіковані, це означає, що зображення орієнтовані під однаковими кутами і мають однаковий масштаб. Для наочності, наведено не ректифіковані зображення (рис. 4.2).

Рисунок 4.2 – Не ректифицированные стереоизображения

Рисунок 4.2 – Не ректифіковані стереозображення

Задача алгоритму полягає в тому, щоб знайти таке зміщення точок лівого (правого) зображення, щоб вони співпали з відповідними точками правого (лівого) зображення. Оскільки зображення вирівняні по горизонталі, то зміщення кожної точки можна представити всього лише одним числом, а саме, число пікселів, на яке потрібно змістити поточний піксель, щоб він відповідав пікселю на іншому зображенні.

Значить рішенням буде двовимірний масив чисел. Його можна зручно представити у графічному вигляді, де значення кожного елемента відповідає яскравості пікселя. Тобто чим більше зміщення, тим більш білою буде виглядати точка в графічному представленні.

Таке графічне представлення рішення називається карта діспарантності (disparity map), карта глибин (depth map), карта зсувів, карта невідповідностей.

Карта діспарантності представлена на малюнку 4.3.

Рисунок 4.3 – Карта диспарантности стереоизображений

Рисунок 4.3 – Карта діспарантності стереозображень

4.2 Способи ректифікації зображень

Для пошуку відповідностей зображень для початку потрібно привести зображення до виду, в якому їх буде зручно порівнювати. Якщо цього не робити, то співставлення зображень займе дуже багато часу, оскільки доведеться перебирати всі можливі повороти зображень і масштаби. Це дуже трудомісткий процес, який може зайняти кілька годин. Щоб значно прискорити співставлення, проводять їх приблизне співставлення.

Найпростішим способом є використання зменшених копій зображень. Після чого проводиться порівняння зображень з різними поворотами і масштабами. Після того, як знайдено найкраще рішення, масштаб зображень збільшується і пошук здійснюється вже з урахуванням обчислених даних. Таким чином, поступово буде обчислена орієнтація вихідного зображення. Цей підхід є простим в реалізації, але не завжди точно визначає орієнтацію і витрачає багато часу.

Іншим підходом є пошук на зображеннях певних характерних особливостей. Наприклад, пошук прямих ліній, або певних ключових точок.

Характерні(ключові) точки можуть знаходитися на кутах об’єктів, на вигинах контурів, різких перепадах яскравості, в центрі однорідних областей і так далі. Одними з популярних методів знаходження ключових точок є методи SIFT, SURF і детектор Харриса.

Пошук ключових точок здійснюється на двох зображеннях. В результаті буде отримано безліч точок з координатами(x, y) для кожного зображення. Після чого треба дізнатися, які саме точки одного зображення відповідають іншим точкам. Треба так само враховувати, що деякі точки не відповідатимуть жодній точці. Зазвичай при виконанні цього завдання використовується кросскорреляційний метод, метод відстаней Евкліда, метод оцінки моделі RANSAC.

В результаті виконання відповідності буде отримана матриця перетворення, яка є звичайною матрицею афінного перетворення. Використовуючи цю матрицю, два зображення легко наводяться до ректифікованих. Починаючи з цього етапу, відбувається безпосередньо обчислення карти.

4.3 Алгоритми побудови карти діспарантності

На рисунку 4.4 представлена анімація ручного співставлення двох рядків зображення. Як бачимо з анімації, коли співпадають одні частини зображення, інші не збігаються. Задача співставлення полягає в співставленні всіх ділянок зображення.

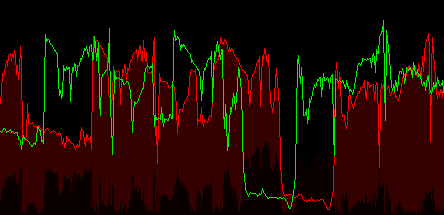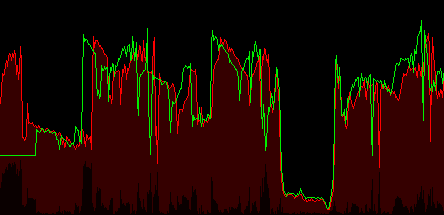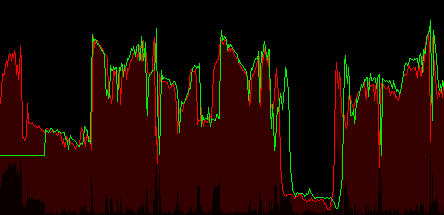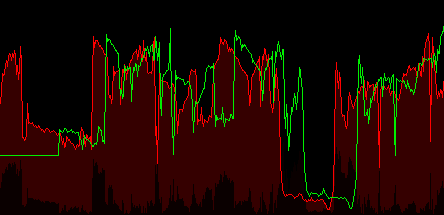
Рисунок 4.4 – Визуализация процесса ручного сопоставления строк изображения

Рисунок 4.4 – Візуалізація процесу ручного співставлення рядків зображення
(анімація містить 7 кадрів, затримка першого кадру 2 секунди, інших - 1 секунда, кількість повторень - 7 разів, розмір файлу 46,2 Кб)

Основна маса робіт по цій темі присвячена розвитку методів, заснованих на кореляційному підході, і методів на основі мінімізації енергії.

Кореляційний підхід полягає в тому, що відбувається порівняння кожної точки одного зображення одного рядка з кожною точкою іншого зображення в тому ж рядку. В результаті порівняння одного рядка отримаємо двовимірний масив кореляцій, в якому менше значення означає найбільш ймовірне рішення. Здійснюючи пошук таких найбільш ймовірних рішень, будується карта діспарантності. Для більш якісних і однозначних рішень, зазвичай порівнюють не одну точку, а відразу кілька сусідніх (наприклад, вікном 8x8 точок).

Алгоритми, які здатні розраховувати карту діспарантності за короткий час, засновані, як правило, на цьому принципі.

Для наочного відображення результату такого порівняння, на рисунку 4.5 приведена матриця кореляцій.

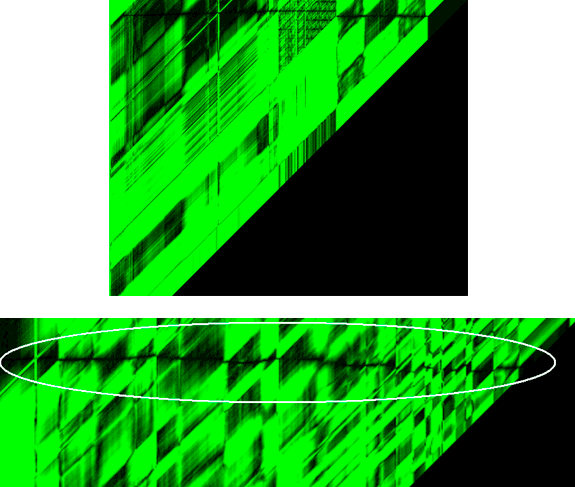
Рисунок 4.5 – Графическое представление результата сравнения строк

Рисунок 4.5 – Графічне представлення результату порівняння рядків

Темна смуга на даному графіку є оптимальним рішенням співставлення зображень. Головна задача правильно виділити її, оскільки в більшості випадків її не так добре видно як на рисунку вище. До того ж потрібно враховувати, що не всі точки будуть мати відповідності, на іншому зображенні такі точки перекриваються іншими об’єктами, що знаходяться ближче до камери.

У методах, заснованих на мінімізації енергії, будується деяка енергетична функція, значення якої залежить від того, які пікселі з одного зображення ставляться у відповідність пікселям з іншого зображення. Ця функція повинна мінімізуватися при правильній відповідності, що призведе до вирішення задачі співставлення. Якість такого підходу набагато вище, ніж кореляційних методів, але такі алгоритми значно довше працюють і значно складніше в реалізації.

Деякі алгоритми засновані на виділенні певних деталей, ділянок, фігур, після чого відбувається пошук відповідностей вже по знайденим ділянкам.

У більшості алгоритмів використовуються не кольорові зображення, а чорно-білі, але деякі використовують інформацію про колір для отримання більш точних результатів. У деяких алгоритмах використовуються ланцюги Маркова.

Існують алгоритми, що представляють зображення у вигляді графа, де вершинами є точки зображення, а ребра є зв’язками між точками. Визначивши ізоморфні пересічення двох графів, буде отримана відповідність між пікселями зображень стереопари.

Досить простим і ефективним методом є динамічне програмування по матриці кореляцій. Найшвидші алгоритми засновані саме на динамічному програмуванні та кореляційному підході.

5. Аналіз алгоритму динамічного програмування і виділення однорідних ділянок

Динамічне програмування (ДП) використовується для порівняння двох послідовностей даних, результатом є така відповідність послідовностей, при якому буде збігатися максимальна кількість даних. Такий алгоритм часто використовується для вирішення завдань нечіткого порівняння послідовностей, рядків тексту, порівняння ланцюгів ДНК, аудіо послідовностей, зображень.

Алгоритм ДП простий в реалізації і дає гарні результати. Розглянемо алгоритм детальніше.

В якості вхідних даних використовується дві горизонтальні рядки лівого і правого зображення. Нехай L (x, y), R (x, y) - яскравість точки з координатами (x, y) для лівого і правого зображення відповідно.

Вихідними даними для ДП є матриця кореляцій Dif [i, j], яка повертає значення різниці пікселя L (i, y) і пікселя R (j, y). Про цю матрицю йшлося раніше (Рис. 4.5). Зазвичай порівняння проводиться не по одному пікселю, а відразу кілька сусідніх, це уточнює результати і зменшує кількість неоднозначних варіантів рішення.

Наступним кроком є обчислення матриці динамічного програмування A [i, j]. На початку алгоритму A [0,0] = 0. Обчислення проводиться для i = 1 .. n, j = 1 .. n, де n - ширина зображення. Елементи даної матриці обчислюються наступним чином:


Minimum = Min( A[i-1,j], A[i,j-1], A[i-1,j-1] )

A[i,j] = Minimum + Dif[i,j].


Функція Min (a, b, c) повертає мінімальне значення аргументів.

Матриця різниць (кореляцій) і матриця динамічного програмування відображені на рисунку 5.1.

Рисунок 5.1 – Матрица разностей и матрица ДП с найденным путем

Рисунок 5.1 – Матриця різниць і матриця ДП із знайденим шляхом

Як видно з рисунку 5.1, якщо по матриці різниць важко точно виділити правильне рішення, то на матриці ДП це рішення чітко виділяється, залишається тільки пройти по цій матриці і знайти цей шлях. Прохід по матриці здійснюється з кінця в початок за наступним алгоритмом:


DisparityMapL [i,y] = j-i

DisparityMapR [j,y] = i-j

Up = A[i-1,j]

Left = A[i,j-1]

UpLeft = A[i-1,j-1]

Minimum = Min( Up,Left,UpLeft )

case Minimum of

UpLeft : i=i-1;j=j-1

Left : j=j-1

Up : i=i-1

end


На початку алгоритму i = n і j = n. Описані вище кроки застосовуються до тих пір, поки i та j приймуть нульові значення. (i, j) визначає положення в матриці ДП. DisparityMapR [x, y] і DisparityMapL [x, y] є обчисленими картами діспарантності для правого і лівого зображень відповідно (достатньо однієї карти).

Як видно з опису, алгоритм простий у реалізації, але в той же час є хорошим і якісним методом пошуку відповідностей стереозображень.

Так само з опису видно, що кожен рядок зображень розглядається незалежно від інших. З одного боку це добре, бо алгоритм можна розподілити на велику кількість процесорів, тим самим збільшивши швидкість обчислення. З іншого боку, відсутність взаємозв’язку з сусідніми рядками викликає ефект гребінки. Цей ефект відображений на рисунку 5.2.

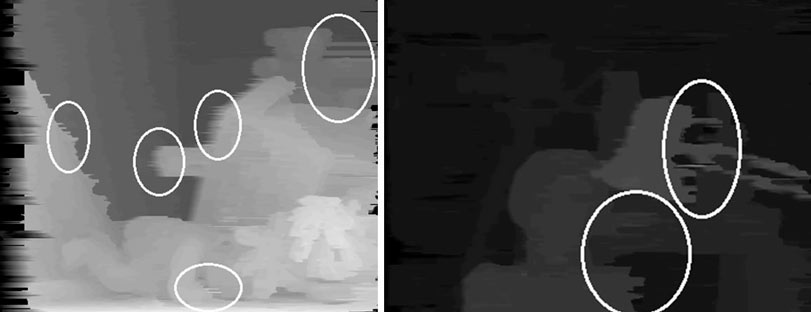
Рисунок 5.2 – Характерный для ДП эффект гребенки на карте диспарантности

Рисунок 5.2 – Характерний для ДП ефект гребінки на карті діспарантності

Такі помилки виникають через те, що зображення містить однорідні ділянки, для яких алгоритм використовує ту ж глибину, як і попередніх точок. Суть алгоритму ДП - робити якомога менше переходів з однієї глибини на іншу, тому в деяких випадках глибина зберігається незмінною там, де це не потрібно.

Алгоритми, що використовують пошук на зображенні однорідних ділянок, краще справляються з такими випадками. Такі алгоритми виділяють певні ділянки, окремі об’єкти і співставляють їх цілком. При такому підході межі будуть більш чіткими та правильними.

Прикладом таких однорідних ділянок можуть бути ділянки, вказані на рисунку 5.3.

Рисунок 5.3 – Пример однородных областей

Рисунок 5.3 – Приклад однорідних ділянок

Такі ділянки можна виділити за допомогою спеціального алгоритму і надалі зробити точну відповідність з такими ж ділянками на іншому зображенні. Такий підхід дозволяє знаходити точну відповідність об’єктів, при цьому зберігаються рівні межі об’єкта.

Недоліком такого підходу можна вважати орієнтованість на однорідні ділянки. Алгоритм повністю залежить від наявності таких ділянок, яких на деяких зображеннях може не бути чи не бути в певних частинах зображення, через що даний алгоритм буде працювати неправильно.

Об’єднавши два підходи, можна використовувати переваги кожного методу і виключити недоліки. Виробляючи пошук однорідних ділянок і їх співставлення можна полегшити і уточнити роботу кореляційного алгоритму. Такий підхід дозволить уточнити роботу алгоритму ДП [20].

Висновки

Поєднання зображень потрібно в багатьох сферах людської діяльності: це і фотограмметрія, і проблеми зору роботів, і завдання побудови систем навігації автономних транспортних засобів, і біомедичні програми. Завдяки великій кількості практичних задач різними авторами було запропонована велика кількість рішень задачі суміщення, характерних для конкретної сфери застосування. Сучасні алгоритми мають спільний недолік - маленька продуктивність якісних алгоритмів, тому ведуться пошуки швидких і ефективних алгоритмів.

В результаті огляду й аналізу існуючих алгоритмів співставлення стереозображень, були виділені основні підходи, які будуть використані у подальшій розробці. В ході проведених досліджень було проаналізовано переваги і недоліки існуючих алгоритмів, особливості стереозображень, характер помилок обчислень, що буде враховуватися при подальшій розробці алгоритму. Подальші дослідження спрямовані на розробку способу визначення і виділення однорідних ділянок, оптимізацію обчислень, прискорення алгоритму шляхом використання вже обчислених даних.


На момент написання реферату магістерська робота ще не є завершеною. Готовий варіант роботи може бути отриманий у автора або його керівника після 20 грудня 2012.


Перелік посилань

  1. Гришин В. А Оценка точности установления соответствия // Доклады 10-ой Международной конференции и выставки "Цифровая обработка сигналов и ее применение", 26-28 марта 2008 года. Серия: Цифровая обработка сигналов и ее применение. Выпуск: Х-2. С. 428-431.
  2. Юрин Д. В. , Крылов А. С. , Волегов Д. Б. , Насонов А . В. , Свешникова Н. В. Методы и алгоритмы совмещения изображений и их применение в задачах восстановления трехмерных сцен и панорам, анализе медицинских изображений, Москва, В МиК МГУ
  3. Волегов Д.Б. , Юрин Д.В. Грубое совмещение изображений по найденным на них прямым линиям // Труды конференции Графикон 2006, Новосибирск., с . 463–466. http://www.graphicon.ru
  4. Свешникова Н.В. Уточнение сеточной модели трехмерной сцены, предварительно восстановленной по малому количеству характеристических точек // Труды конференции Графикон 2007, Москва 2007, http://www.graphicon.ru
  5. Свешникова Н.В. , Юрин Д.В. Алгоритмы факторизации: достоверность результата и применение для восстановления эпиполярной геометрии // Труды конференции Графикон 2006, Новосибирск., с. 158–165.
  6. А.В. Агарков Построение карты диспаратности на основе сравнения графов, Институт проблем искусственного интеллекта, г. Донецк, Украина , 2006
  7. А.В. Агарков Иерархическое представление изображения  с помощью графа, Институт проблем искусственного интеллекта, г. Донецк, Украина, 2003
  8. Henkel R.D. Fast Stereovision by Coherence Detection / Ed. by G. Sommer, K. Daniilidis, J. Pauli // Proc. of the 7th International Conf. on Computer Analysis of Images and Patterns, CAIP'97 in Kiel, LNCS 1296, Springer. – Berlin. – 1997. – P. 297-304.
  9. Stefano L.D., Marchionni M., Mattoccia S., Neri G. A Fast Area-Based Stereo Matcting Algorithm //  Proc. of 15th International Conf. on Vision Interface. – 2002. – P. 146-153.
  10. Egnal G., Mintz M., Daniilidis K. Limiting the Search Rang of Correlation Stereo Using Silhouettes // Proc. of 15th International Conf. on Vision Interface. – 2002. – P. 170-177.
  11. Boufama B., Jin K. Towards a Fast and Reliable Dense Matcing Algorithm // Proc. of 15th International Conf. on Vision Interface. – 2002. – P. 178-185.
  12. Hirschmuller H. Improvements in Real-Time Correlation-Based Stereo Vision // CVPR 2001 Stereo Workshop / IJCV. – 2002.
  13. Muhlmann K., Maier D., Hesser J., Manner R. Calculating Dense Disparity Maps from Color Stereo Images, an Efficient Implementation // CVPR 2001 Stereo Workshop / IJCV 2002.
  14. Boykov Yu., Veksler O., Zabih R. A New Algorithm for Energy Minimization with Discontinuities // EMMCVPR. – 1999. – P. 205-220.
  15. Kolmogorov V., Zabih R. Computing Visual Correspondence with Occlusions via Graph Cuts  // ICCV. – 2001. – P. 508-515.
  16. Kawai Y., Ueshiba T., Ishiyama Y., Sumi Y., Tomita F. Stereo Correspondence Using Segment Connectivity // Proc. 14th International Conf. on Pattern Recognition, ICPR'98.  – Brisbane (Australia). – 1998. – P. 648-651.
  17. Построение SIFT дескрипторов и задача сопоставления изображений [электронный ресурс]. – Режим доступа: http://habrahabr.ru/post/106302/
  18. Обнаружение устойчивых признаков изображения: метод SURF [электронный ресурс]. – Режим доступа: http://habrahabr.ru/post/103107/
  19. Динамическое программирование [электронный ресурс]. – Режим доступа: http://rain.ifmo.ru/cat/view.php/...
  20. Чигарев И.А. Разработка алгоритма сопоставления стереоизображений и построения карты диспарантности // Современная информационная Украина: информатика, экономика, философия / Материалы VI Международной научно-практической конференции молодых ученых, аспирантов, студентов. - Донецк, ДонНТУ - 2012.