ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Проблема якості даних є на сьогоднішній день однією з найважливіших проблем, що вирішуються при побудові інтелектуальних систем. Особливо гостро дана проблема проявляється при побудові навчаючих систем розпізнавання як самостійних систем або підсистем інтелектуальних систем верхнього рівня. Від якості вихідних даних залежить не тільки достовірність функціонування системи в майбутньому, але і можливість її навчання в принципі [1].

Основною відмінністю навчаючих систем розпізнавання є побудова класифікатора в результаті навчання. Процес навчання полягає в послідовному предʼявленні системі безлічі вихідних обʼєктів і коригування класифікатора відповідно до цими обʼєктами [2]. Саме тому попередня обробка даних є найважливішим етапом побудови систем розпізнавання.

Процес дослідження, фільтрації, перетворення і моделювання даних з метою отримання корисної інформації та прийняття рішень прийнято називати інтелектуальним аналізом даних або Data Mining [3].

У даній роботі вихідні дані подаються у вигляді таблиці, рядки якої відповідають обʼєктам, дані про які апріорно відомі при побудові системи, а стовпці – ознаками (властивостями, характеристикам) цих обʼєктів. Таку таблицю разом з вказівку номера класу, до якого відноситься кожен з обʼєктів, прийнято називати навчальною вибіркою.

1.1 Актуальність роботи

Актуальність даної роботи підтверджується кількістю різноманітних методів передобробки даних, розроблених за останні роки. Це повʼязано насамперед із суттєвим розширенням кола прикладних задач, що вирішуються шляхом побудови інтелектуальних систем і, в тому числі, систем розпізнавання образів. Багато сучасні системи повинні обробляти десятки і сотні тисяч обʼєктів за мінімальний час, тому від передобробки цих обʼєктів залежить ефективність систем в цілому. Саме тому завдання фільтрації даних є актуальнм науково-технічним завданням, що вимагає розробки сучасних підходів до її вирішення.

1.2 Мета і завдання дослідження

Обʼєктом дослідження є завдання фільтрації даних в обучаючих системах розпізнавання.

Предметом дослідження – методи визначення та видалення викидів в навчальних вибірках.

Метою випускної роботи магістра є дослідження існуючих методів визначення шуму в даних і розробка методу видалення викидів в навчальних вибірках.

У процесі роботи необхідно вирішити наступні завдання:

1) дослідження етапів побудови навчаючих систем розпізнавання і способів передобробки навчальних вибірок;

2) дослідження методів видалення викидів з навчальних вибірок та критеріїв зупину фільтрації даних;

3) розробка методу видалення викидів з даних на основі аналізу зважених навчальних вибірок;

4) розробка програмної системи для аналізу ефективності запропонованого методу фільтрації даних.

1.3 Передбачувана наукова новизна

Науковою новизною даної роботи є розробка методу видалення викидів на основі аналізу зважених навчальних вибірок – нового напряму в передобробці навчальних вибірок великого обсягу, ефективно вирішального проблеми стиснення і обʼєднання навчальних даних

1.4 Практична значущість

Практична значущість даної роботи полягає в розробці методу фільтрації даних, що дозволяє підвищити якість вихідної безлічі даних і, як наслідок, ефективність роботи всієї системи в цілому.

Використання зважених навчальних вибірок, вирішальних для навчальних вибірок великого розміру завдання стиснення і обʼєднання даних, дозволить запропонувати єдиний метод, що включає в себе виконання всіх трьох способів передобробки даних.

2. Огляд і аналіз методів видалення викидів у даних

2.1 Види передобробки даних

Рішення задач розпізнавання образів традиційно складається з трьох послідовно виконуваних етапів [4] (малюнок 1):

1) отримання даних від вимірників;

2) попередня обробка даних;

3) побудова класифікатора та виконання класифікації.

Завдання отримання даних від вимірників є специфічним завданням, розвʼязуваної в рамках розглянутої прикладної області. Вирішенню завдання побудови класифікатора та виконання класифікації присвячено більшість робіт з теорії створення систем розпізнавання, що розглядають різні методи класифікації. Вибір методу побудови вирішальних правил (класифікаторів) значною мірою залежить від особливостей аналізованих обʼєктів, тому розробка методів передобробки даних в системах розпізнавання є одним з найбільш важливих і інтенсивно розвиваються напрямків Data Mining [4, 5].

Малюнок 1 – Етапи інтелектуального аналіза даних

Попередня обробка даних в системах розпізнавання є ітеративним процесом і включає [4]:

1) стиснення даних, що включає в себе знаходження мінімального ознакового простору і репрезентативного безлічі даних на основі методів редукції і трансформації;

2) стиснення даних, що включає в себе знаходження мінімального ознакового простору і репрезентативного безлічі даних на основі методів редукції і трансформації;

3) обʼєднання даних, що дозволяє зменшити обсяг даних зі збереженням початкової інформації за допомогою евристичних алгоритмів.

Побудова сучасних систем розпізнавання передбачає виконання одного або декількох етапів передобробки даних за одну або декілька ітерацій. За результатами передобробки формується безліч даних (навчальна вибірка) у вихідному або модифікованому поданні, безпосередньо використовуване для побудови вирішальних правил класифікації. У більшості систем попередня обробка даних полягає в їх очищенню, при виконанні якої найбільша увага приділяється видаленню шуму (викидів) і даних низької якості.

2.2 Поняття викиду і проблеми його визначення

У загальному випадку викидом прийнято називати обʼєкт деякого класу, значення ознак якого істотно відрізняються від значень ознак обʼєктів цього ж класу [7]. Такі обʼєкти в просторі ознак знаходяться в оточенні обʼєктів іншого класу і, як наслідок, погіршують якість вирішальних правил класифікації. Пошук викидів здійснюється за допомогою фільтрів – процедур, що дозволяють виділяти релевантну інформацію в наявних початкових даних [8]. Задача побудови фільтрів – це зухвало складна задача. До найбільш важливих питань, що виникають при побудові фільтрів, відносяться [8]:

– відділення шуму від обʼєктів-винятків, що вимагають окремої інтерпретації і характеризують деяку особливість класу;

– облік неузгодженості різних методів побудови класифікаторів у віднесенні обʼєктів до викидів або шумів (наприклад, одні й ті ж навчальні дані вирішальним правилом, побудованим по одному методу, можуть класифікуватися як шум, а з іншого – як цінна навчальна інформація);

– виявлення шуму, що має систематичний характер появи в навчальній вибірці;

– виявлення і видалення викидів, відсутність яких у вибірці не призводить поліпшення якості навчання (у цьому випадку видалення викидів може привести до погіршення якості класифікації побудованим вирішальним правилом через зменшення обсягу вибірки).

– розробка фільтрів, що враховують природу міститься в навчальній вибірці інформації. Поряд з проблемою пошуку і видалення викидів існує проблема вибору критерію зупину фільтрації даних, тому що видалення нешумових обʼєктів зменшить навчальну вибірку і, як наслідок, суттєво погіршить якість отримуваних в результаті навчання вирішальних правил класифікації.

2.3 Класифікація і аналіз методів видалення викидів у даних

Основним принципом виділення викидів в навчальних вибірках є відповідність даних гіпотезі компактності, яка полягає в тому, що обʼєкти одного і того ж класу відображаються в просторі ознак в геометрично близькі точки, утворюючи «компактні» згустки [9].

Методи пошуку та обробки знайдених викидів можуть бути розділені на дві групи [7]. Методи першої групи спрямовані на коригування викидів шляхом зміни значень з ознак, що дозволяє зберегти розмір вибірки, але може приводити до помилок через невірну коригування. Методи другої групи видаляють викиди шляхом фільтрації даних, що може призводити до її зменшення на 10-15% і, як підкреслювалося раніше, у разі невірного вибору критерію зупину фільтрації погіршити ефективність класифікації.

Оскільки завдання очищення даних є однією з трьох завдань, що вирішуються при передобробці вихідних навчальних вибірок, для її вирішення часто використовують алгоритми стиснення та обʼєднання даних.

Завдання стиснення і обʼєднання даних за умови незмінних словника ознак можуть бути вирішені двома способами. Перший спосіб полягає у відборі деякого безлічі обʼєктів вихідної навчальної вибірки, кожен з яких відповідає поставленим вимогам. Найбільш відомими алгоритмами, що реалізують такий спосіб, є алгоритми STOLP [6], FRiS-STOLP [10], NNDE (Nearest Neighbor Density Estimate) і MDCA (Multiscale Data Condensation Algorithm) [4].

Основою алгоритму STOLP є відшукання найбільш «напружених» прикордонних точок навчальної вибірки. З цією метою для кожної точки визначаються відстані до найближчої точки свого образу і найближчої точки чужого образу. Відношення характеризує величину ризику для даної точки бути розпізнаної як точки чужого образу. Серед точок кожного образу вибирається по одній точці з максимальним значенням величини. Ці точки заносяться в список прецедентів.

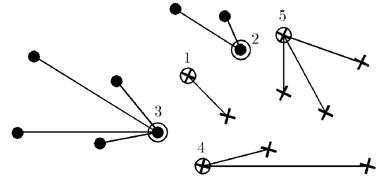
Малюнок 2 – Результат роботи алгоритму STOLP

Потім робиться пробне розпізнавання всіх точок навчальної вибірки з опорою на прецеденти і з використанням правила найближчого сусіда: точка ставиться до того образу, відстань до прецеденту якого мінімально. Серед точок, розпізнаних неправильно, вибирається точка з максимальним значенням і нею поповнюється список прецедентів, після чого повторюється процедура пробного розпізнавання усіх точок. Так продовжується до тих пір, поки всі крапки навчальної вибірки не стануть розпізнаватися без помилок. Результат роботи алгоритму STOLP наведено на малюнку 2.

Другий спосіб полягає в побудові безлічі нових обʼєктів, кожен з яких будується за інформацією про деяке підмножині обʼєктів вихідної навчальної вибірки та узагальнює його. До алгоритмам такого типу можна віднести, наприклад, алгоритм ДРЕТ [6], що покриває просторі ознак безліччю пересічних кіл, визначаючи тим самим області, що належать кожному з класів, алгоритми LVQ (learning vector quantization) [11] і w-GridDC [12].

Метод «дробящіхся еталонів» (алгоритм Дред) заснований на покритті обʼєктів кожного з класів простими фігурами, усложняющимися в міру необхідності. Один з найбільш часто використовуваних варіантів реалізації цього методу передбачає використання в якості покривають фігур набору гіперсфери. Для кожного класу будується гіперсфери мінімального радіусу, що покриває всі обʼєкти навчальної вибірки даного класу. Значення радіусів цих сфер і відстані між їх центрами дозволяють визначити класи, сфери яких не перетинаються зі сферами інших класів. Такі сфери вважаються еталонними (класи 1 і 8 на малюнку 3), а їх центри та радіуси запамʼятовуються як еталони першого покоління.

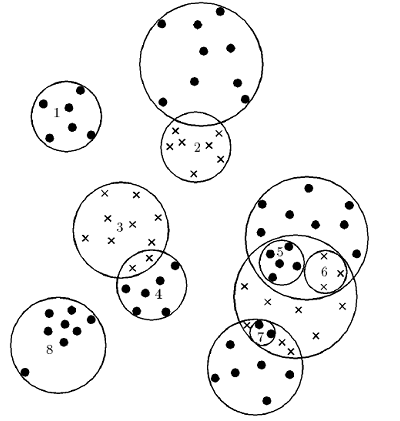
Малюнок 3 – Зменшення розміру навчальної вибірки з використанням алгоритму Дред

Якщо дві сфери перетинаються, але в області перетину не залишилося ні одного обʼєкта навчальної вибірки, то такий перетин вважається фіктивним, а центри та радіуси цих сфер також заносяться в список еталонів першого покоління. При цьому область перетину вважається належить сфері меншого радіуса (клас 2 на малюнку 3).

Якщо в області перетину виявилися тільки обʼєкти одного з класів, то ця зона вважається належить того класу, до якого відносяться і обʼєкти цієї зони (клас 3 на малюнку 3). Обʼєкт вважається належать до класу 4, якщо він потрапляє в сферу 4 і не потрапляє в сферу 3.

Якщо ж область перетину сфер містить обʼєкти різних класів, то для цих обʼєктів будуються еталони другого покоління (сфери 5, 6 і 7). Якщо і вони перетинаються, то для обʼєктів зони їх перетину будуються еталони третього покоління. Процедура побудови еталонів триває до поділу всіх обʼєктів навчальної вибірки гіперсфери.

3. Побудова зважених навчальних вибірок

Поряд із завданням очищення даних, як було сказано раніше, попередня обробка включає в себе завдання стиснення і обʼєднання даних з метою зменшення впливу викидів на ефективність роботи системи і зменшення обсягу збережених даних.

Одним з найбільш ефективних методів стиснення і обʼєднання даних є метод w-GridDC [12] побудови виваженої скороченою навчальної вибірки w-обʼєктів.

Ідеєю методу w-GridDC є накладення сітки на просторі ознак для формування безлічі клітин, визначення обʼєктів вибірки, що належать кожній з клітин та їх заміна на w-об'єкти. Формування обʼєктів нової вибірки виконується тільки в разі належності всіх обʼєктів клітини одного класу. Вага w-обʼєктів визначається за кількістю обʼєктів вихідної вибірки, що належать клітці.

Далі наведемо покроковий опис методу.

Крок 1. Формування сітки. Розраховується крок клітини s за формулою:

где max{xi} – максимальне значення i-тої ознаки серед усіх обʼєктів вибірки;

min{xi} – мінімальне значення.

Виконується розбиття ознакового простору по кожному з ознак на інтервали довжиною (накладення прямокутної сітки), результатом якого є безліч клітин.

Далі для кожного обʼєкта вибірки визначається клітина, якій цей обʼєкт належить. Обʼєкт належить деякій клітці тоді і тільки тоді, коли кожне з значень його ознак входить в інтервал значень відповідних ознак даної клітини. В результаті формування сітки та обробки обʼєктів вихідної навчальної вибірки будуть сформовані непересічні підмножини обʼєктів, що належать клітці.

Крок 2. Формування значень ознак w-обʼєктів.

Можливі такі варіанти обробки вмісту клітин.

1. Якщо всі обʼєкти клітини належать до одного класу, то значення ознак обʼєкта нової вибірки розраховуються як координати центру мас обʼєктів цієї клітини:

2. Якщо клітина не містить жодного об'єкта, то обʼєкт нової вибірки не формується.

3. Якщо клітина містить обʼєкти декількох класів, то вона ділиться на дві рівні за розміром клітини (по черзі вертикально або горизонтально) до тих пір, поки будь-яка з клітин усередині початкової клітини не буде містити обʼєкти тільки одного класу. Далі по кожній з отриманих клітин формуються обʼєкти нової вибірки (згідно випадків 1 і 2).

Класифікація w-обʼєкта визначається за класифікацією обʼєктів, по яких він сформований.

Крок 3. Визначення ваги w-обʼєктів. Вага w-обʼєкта дорівнює кількості обʼєктів вихідної вибірки, що належать клітині, тобто

В результаті виконання алгоритму буде отримана зважена навчальна вибірка w-обʼєктів.

Аналіз особливостей розподілу ваг w-обʼєктів, виконаний в [13], показує, що з віддаленням від міжкласової кордону вага більшості w-об'єктів експоненціально збільшується. Поблизу міжкласової кордону більшість w-обʼєктів мають меншу вагу. У той же час у зваженій вибірці є деяка кількість обʼєктів, що мають одиничний або близький до нього вагу. Аналіз таких w-обʼєктів і є способом визначення викидів по вибірках w-обʼєктів.

Далі наведемо покроковий опис методу (малюнок 4). У результаті виконання алгоритма буде отримана зважена навчальна вибірка

Побудова вибірки w-обʼєктів на основі алгоритму w-GridDC

Рисунок 2 – Побудова вибірки w-обʼєктів на основі алгоритму w-GridDC
(анімація: 4 кадра, 5 циклів повторення, 130 кілобайт)

4. Висновки

В ході проведення досліджень були проаналізовані етапи побудови навчаються систем розпізнавання в цілому і види передобробки даних зокрема. Було показано, що для сучасних інтелектуальних систем рішення задач передобробки даних має першорядне значення через великий обсяг і різнорідності вхідної інформації. За результатами проведеного аналізу в якості обʼєкта дослідження обрано завдання фільтрації даних, що представляє собою одну з найбільш актуальних завдань Data Mining і використовується при вирішенні багатьох прикладних задач.

Виконано аналіз існуючих методів визначення викидів в навчальній вибірці, що показав, що найбільший вплив на вибір шумових обʼєктів в силу гіпотези компактності надає топологічний розподіл обʼєктів навчальної вибірки в просторі ознак.

Одними з найбільш ефективних алгоритмів передобробки даних, заснованих на аналізі взаємного розташування обʼєктів навчальної вибірки в просторі ознак, є алгоритми w-baseWTS і w-GridDC побудови зважених навчальних вибірок w-обʼєктів, тому розробку нового методу видалення викидів в даних планується виконувати на основі зважених навчальних вибірок.

5. Список літератури

  1. Крисилов В.А., Юдин С.А., Олешко Д.Н. Использование гипотезы – компактности при построении обучающей выборки для прогнозирующих нейросетевых моделей // System Research & Information Technologies. – 2006. – № 3. – С. 26 – 37.
  2. Дуда Р., Харт П. Распознавание образов и анализ сцен. – М.: Мир, 1976. – 512 с.
  3. Профессиональный информационно-аналитический ресурс, посвященный машинному обучению, распознаванию образов и интеллектуальному анализу данных – Интеллектуальный анализ данных [Электронный ресурс].–Режим доступа: http://www.machinelearning.ru
  4. Larose D.T. Discovering knowledge in Data: An Introduction to Data Mining / D.T. Larose – New Jersey, Wiley & Sons, 2005. – 224 p.
  5. Pal S.K. Pattern Recognition Algorithms for Data Mining: Scalability, Knowledge Discovery and Soft Granular Computing / S.K. Pal, P. Mitra – Chapman and Hall/CRC, 2004. – 280 p.
  6. Загоруйко Н.Г. Методы распознавания и их применение. – М.: Сов. радио, 1972. – 208 с.
  7. Волченко Е.В., Кузьменко И.Ю. Анализ методов нахождения выбросов в обучающих выборках // Проблеми інформатики і моделювання. Тезиси одинадцятої міжнародної науково-технічної конференції. Секція "Молоді вчені". – Х.: НТУ "ХПІ", 2011. – С. 12 – 13.
  8. Дюличева Ю.Ю. О задачах фильтрации обучающих данных // Искусственный интеллект. – 2006. – № 2. – 65 – 71.
  9. Загоруйко Н.Г. Гипотезы компактности и -компактности в методах анализа данных // Сибирский журнал индустриальной математики. – 1998. – №1. – Том 1. – С. 114 – 126.
  10. Zagoruiko N.G., Borisova I.A., Dyubanov V.V., Kutnenko O.A. Methods of Recognition Based on the Function of Rival Similarity // Pattern Recognition and Image Analysis. – 2008. – Vol. 18. – №.1. – P. 1–6.
  11. Kohonen T. Self-Organizing Maps. – Springer-Verlag, 1995. – 501 р.
  12. Волченко Е.В. Сеточный подход к построению взвешенных обучающих выборок w-объектов в адаптивных системах распознавания // Вісник Національного технічного університету "Харківський політехнічний інститут". Збірник наукових праць. Тематичний випуск: Інформатика i моделювання. – Харків: НТУ "ХПІ", 2011. – № 36. – С. 12 – 22.
  13. Volchenko E.V. Research of features in association of training sample objects to meta-objects // 9th International Conference on “Pattern recognition and image analysis: new information technologies”: Conference Proceeding. Nizhny Novgorod, Russian Federation, 2008. – Vol. 2. – P. 291-294.

    6. Важливе зауваження

    При написанні даного автореферату магістерська робота ще не завершена. Можлива дата завершення - 10 грудня 2012р. Повний текст роботи, а також матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.