Реферат по теме выпускной работы
Содержание
- Введение
- 1.1 Актуальность работы
- 1.2 Цель и задачи исследования
- 1.3 Предполагаемая научная новизна
- 1.4 Практическая значимость
- 2. Обзор и анализ методов удаления выбросов в данных
- 2.1 Виды предобработки данных
- 2.2 Понятие выброса и проблемы их определения
- 2.3 Классификация и анализ методов удаления выбросов в данных
- 3. Построение взвешенных обучающих выборок
- 4. Выводы
- 5. Список литературы
- 6. Важное замечание
- 1.4 Практическая значимость
Введение
Проблема качества данных является на сегодняшний день одной из важнейших проблем, решаемых при построении интеллектуальных систем. Особенно остро данная проблема проявляется при построении обучающихся систем распознавания как самостоятельных систем или подсистем интеллектуальных систем верхнего уровня. От качества исходных данных зависит не только достоверность функционирования системы в будущем, но и возможность её обучения в принципе [1].
Основным отличием обучающихся систем распознавания является построение классификатора в результате обучения. Процесс обучения заключается в последовательном предъявлении системе исходного множества объектов и корректировки классификатора в соответствии с этими объектами [2]. Именно поэтому предобработка данных является важнейшим этапом построения систем распознавания.
Процесс исследования, фильтрации, преобразования и моделирования данных с целью извлечения полезной информации и принятия решений принято называть интеллектуальным анализом данных или Data Mining [3].
В данной работе исходные данные представляются в виде таблицы, строки которой соответствуют объектам, данные о которых априорно известны при построении системы, а столбцы – признакам (свойствам, характеристикам) этих объектов. Такую таблицу вместе с указание номера класса, к которому относится каждый из объектов, принято называть обучающей выборкой.
1.1 Актуальность работы
Актуальность данной работы подтверждается количеством разнообразных методов предобработки данных, разработанных за последние годы. Это связано прежде всего с существенным расширением круга прикладных задач, решаемых путем построения интеллектуальных систем и, в том числе, систем распознавания образов. Многие современные системы должны обрабатывать десятки и сотни тысяч объектов за минимальное время, а предобработки этих объектов зависит эффективность систем в целом. Именно поэтому задача фильтрации данных является актуальной научно-технической задачей, требующей разработки современных подходов к её решению.
1.2 Цель и задачи исследования
Объектом исследования является задача фильтрации данных в обучающихся системах распознавания.
Предметом исследования – методы определения и удаления выбросов в обучающих выборках.
Целью выпускной работы магистра является исследование существующих методов определения шума в данных и разработка метода удаления выбросов в обучающих выборках.
В процессе работы необходимо решить следующие задачи:
1) исследование этапов построения обучающихся систем распознавания и способов предобработки обучающих выборок;
2) исследование методов удаления выбросов из обучающих выборок и критериев останова фильтрации данных;
3) разработка метода удаления выбросов из данных на основе анализа взвешенных обучающих выборок;
4) разработка программной системы для анализа эффективности предложенного метода фильтрации данных.
1.3 Предполагаемая научная новизна
Научной новизной данной работы является разработка метода удаления выбросов на основе анализа взвешенных обучающих выборок – нового направления в предобработке обучающих выборок большого объема, эффективно решающего проблемы сжатия и объединения обучающих данных
1.4 Практическая значимость
Практическая значимость данной работе состоит в разработке метода фильтрации данных, позволяющего повысить качество исходного множества данных и, как следствие, эффективность работы все системы в целом.
Использование взвешенных обучающих выборок, решающих для обучающих выборок большого размера задачи сжатия и объединения данных, позволит предложить единый метод, включающей в себя выполнение всех трех способов предобработки данных.
2. Обзор и анализ методов удаления выбросов в данных
2.1 Виды предобработки данных
Решение задач распознавания образов традиционно состоит из трех последовательно выполняемых этапов (рисунок 1):
1) получение данных от измерителей;
2) предобработка данных;
3) построение классификатора и выполнение классификации.
Задача получения данных от измерителей является специфической задачей, решаемой в рамках рассматриваемой прикладной области. Решению задачи построения классификатора и выполнения классификации посвящено большинство работ по теории создания систем распознавания, рассматривающих различные методы классификации. Выбор метода построения решающих правил (классификаторов) в значительной мере зависит от особенностей рассматриваемых объектов, поэтому разработка методов предобработки данных в системах распознавания является одним из наиболее важных и интенсивно развивающихся направлений Data Mining [4, 5].
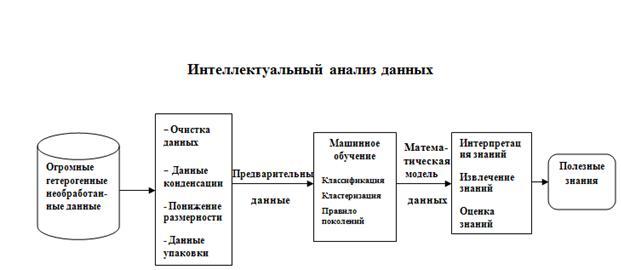
Рисунок 1 – Этапы интеллектуального анализа данных
Предобработка данных в системах распознавания является итеративным процессом и включает [4]:
1) очистку данных, которая заключается в удалении шума, пропусков в данных и данных низкого качества;
2) сжатие данных, включающее в себя нахождение минимального признакового пространства и репрезентативного множества данных на основе методов редукции и трансформации;
3) объединение данных, позволяющее уменьшить объем данных с сохранением исходной информации с помощью эвристических алгоритмов.
Построение современных систем распознавания предполагает выполнение одного или нескольких этапов предобработки данных за одну или несколько итераций. По результатам предобработки формируется множество данных (обучающая выборка) в исходном или модифицированном представлении, непосредственно используемое для построения решающих правил классификации. В большинстве систем предобработка данных заключается в их очистке, при выполнении которой наибольшее внимание уделяется удалению шума (выбросов) и данных низкого качества.
2.2 Понятие выброса и проблемы их определения
В общем случае выбросом принято называть объект некоторого класса, значения признаков которого существенно отличаются от значений признаков объектов этого же класса. Такие объекты в пространстве признаков находятся в окружении объектов другого класса и, как следствие, ухудшают качество решающих правил классификации [1]. Поиск выбросов осуществляется с помощью фильтров - процедур, позволяющих выделять релевантную информацию в имеющихся начальных данных. Задача построения фильтров – это вызывающе сложная задача. К наиболее важным вопросам, возникающим при построении фильтров являются:
– отделение шума от объектов-исключений, требующих отдельной интерпретации и характеризующих некоторую особенность класса;
– учет несогласованности различных методов построения классификаторов в отнесении объектов к выбросам или шумам (например, одни и те же обучающие данные решающим правилом, построенным по одному методу, могут классифицироваться как шум, а по другому – как ценная обучающая информация);
– выявление шума, имеющего систематический характер появления в обучающей выборке;
– выявление и удаление выбросов, отсутствие которых в выборке не приводит улучшению качества обучения (в этом случае удаление выбросов может привести к ухудшению качества классификации построенным решающим правилом из-за уменьшения объема выборки).
– разработка фильтров, учитывающих природу содержащейся в обучающей выборке информации. Наряду с проблемой поиска и удаления выбросов существует проблема выбора критерия останова фильтрации данных, т.к. удаление нешумовых объектов уменьшит обучающую выборку и, как следствие, существенно ухудшит качество получаемых в результате обучения решающих правил классификации.
2.3 Классификация и анализ методов удаления выбросов в данных
Основным принципом выделения выбросов в обучающих выборках является соответствие данных гипотезе компактности, которая состоит в том, что объекты одного и того же класса отображаются в признаковом пространстве в геометрически близкие точки, образуя «компактные» сгустки [9].
Методы поиска и обработки найденных выбросов могут быть разделены на две группы [7]. Методы первой группы направлены на корректировку выбросов путем изменения значений из признаков, что позволяет сохранить размер выборки, но может приводить к ошибкам из-за неверной корректировки. Методы второй группы удаляют выбросы путем фильтрации данных, что может приводить к её уменьшению на 10-15% и, как подчеркивалось ранее, в случае неверного выбора критерия останова фильтрации ухудшить эффективность классификации.
Поскольку задача очистки данных является одной из трех задач, решаемых при предобработке исходных обучающих выборок, для её решения зачастую используют алгоритмы сжатия и объединения данных.
Задачи сжатия и объединения данных при условии неизменяющегося словаря признаков могут быть решены двумя способами. Первый способ заключается в отборе некоторого множества объектов исходной обучающей выборки, каждый из которых отвечает предъявляемым требованиям. Наиболее известными алгоритмами, реализующими такой способ, являются алгоритмы STOLP [6], FRiS-STOLP [10], NNDE (Nearest Neighbor Density Estimate) и MDCA (Multiscale Data Condensation Algorithm) [4].
Основой алгоритма STOLP является отыскание самых «напряженных» пограничных точек обучающей выборки. С этой целью для каждой точки определяются расстояния до ближайшей точки своего образа и ближайшей точки чужого образа . Отношение характеризует величину риска для данной точки быть распознанной в качестве точки чужого образа. Среди точек каждого образа выбирается по одной точке с максимальным значением величины . Эти точки заносятся в список прецедентов.
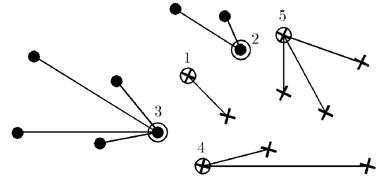
Рисунок 2 – Результат работы алгоритма STOLP
Затем делается пробное распознавание всех точек обучающей выборки с опорой на прецеденты и с использованием правила ближайшего соседа: точка относится к тому образу, расстояние до прецедента которого минимально. Среди точек, распознанных неправильно, выбирается точка с максимальным значением и ею пополняется список прецедентов, после чего повторяется процедура пробного распознавания всех точек. Так продолжается до тех пор, пока все точки обучающей выборки не станут распознаваться без ошибок. Результат работы алгоритма STOLP приведен на рисунке 2.
Второй способ состоит в построении множества новых объектов, каждый из которых строится по информации о некотором подмножестве объектов исходной обучающей выборки и обобщает его. К алгоритмам такого типа можно отнести, например, алгоритм ДРЭТ [6], покрывающий признаковое пространство множеством пересекающихся окружностей, определяя тем самым области, принадлежащие каждому из классов, алгоритмы LVQ (learning vector quantization) [11] и w-GridDC [12].
Метод «дробящихся эталонов» (алгоритм ДРЭД) основан на покрытии объектов каждого из классов простыми фигурами, усложняющимися по мере необходимости. Один из наиболее часто используемых вариантов реализации этого метода предусматривает использование в качестве покрывающих фигур набора гиперсфер. Для каждого класса строится гиперсфера минимального радиуса, покрывающая все объекты обучающей выборки данного класса. Значения радиусов этих сфер и расстояния между их центрами позволяют определить классы, сферы которых не пересекаются со сферами других классов. Такие сферы считаются эталонными (классы 1 и 8 на рисунке 3), а их центры и радиусы запоминаются в качестве эталонов первого поколения.
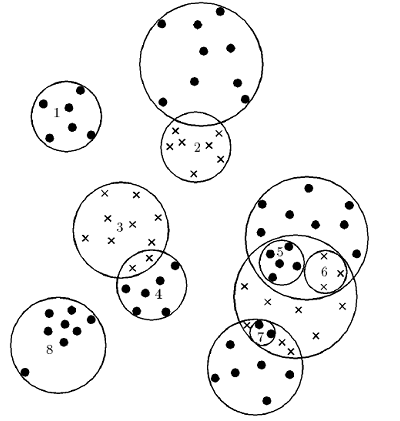
Рисунок 3 – Уменьшение размера обучающей выборки с использованием алгоритма ДРЭД
Если две сферы пересекаются, но в области пересечения не осталось ни одного объекта обучающей выборки, то такое пересечение считается фиктивным, а центры и радиусы этих сфер также заносятся в список эталонов первого поколения. При этом область пересечения считается принадлежащей сфере меньшего радиуса (класс 2 на рисунке 3).
Если в области пересечения оказались только объекты одного из классов, то эта зона считается принадлежащей тому классу, к которому относятся и объекты этой зоны (класс 3 на рисунке 3). Объект считается относящимся к классу 4, если он попадает в сферу 4 и не попадает в сферу 3.
Если же область пересечения сфер содержит объекты разных классов, то для этих объектов строятся эталоны второго поколения (сферы 5, 6 и 7). Если и они пересекаются, то для объектов зоны их пересечения строятся эталоны третьего поколения. Процедура построения эталонов продолжается до разделения всех объектов обучающей выборки гиперсферами.
3. Построение взвешенных обучающих выборок
Наряду с задачей очистки данных, как было сказано ранее, предобработка включает в себя задачи сжатия и объединения данных с целью уменьшения влияния выбросов на эффективность работы системы и уменьшения объема хранимых данных.
Одним из наиболее эффективных методов сжатия и объединения данных является метод w-GridDC [12] построения взвешенной сокращенной обучающей выборки w-объектов.
Идеей метода w-GridDC является наложение сетки на признаковое пространство для формирования множества клеток, определение объектов выборки, принадлежащих каждой из клеток и их замена на w-объекты. Формирование объектов новой выборки выполняется только в случае принадлежности всех объектов клетки одному классу. Вес w-объектов определяется по количеству объектов исходной выборки, принадлежащих клетке.
Далее приведем пошаговое описание метода.
Шаг 1. Формирование сетки. Рассчитывается шаг клетки s по формуле:

где max{xi} – максимальное значение i-ого признака среди всех объектов выборки;
min{xi} – минимальное значение.
Выполняется разбиение признакового пространства по каждому из признаков на интервалы длиной (наложение прямоугольной сетки), результатом которого является множество клеток . Далее для каждого объекта выборки определяется клетка, которой этот объект принадлежит. Объект принадлежит некоторой клетке тогда и только тогда, когда каждое из значений его признаков входит в интервал значений соответствующих признаков данной клетки.
В результате формирования сетки и обработки объектов исходной обучающей выборки будут сформированы непересекающиеся подмножества объектов, принадлежащих клетке.
Шаг 2. Формирование значений признаков w-объектов.
Возможны следующие варианты обработки содержимого клеток.
1. Если все объекты клетки принадлежат к одному классу, то значения признаков объекта новой выборки рассчитываются как координаты центра масс объектов этой клетки:

2. Если клетка не содержит ни одного объекта, то объект новой выборки не формируется.
3. Если клетка содержит объекты нескольких классов, то она делится на две равные по размеру клетки (поочередно вертикально или горизонтально) до тех пор, пока любая из клеток внутри начальной клетки не будет содержать объекты только одного класса. Далее по каждой из полученных клеток формируются объекты новой выборки (согласно случаям 1 и 2).
Классификация w-объекта определяется по классификации объектов, по которым он сформирован.
Шаг 3. Определение веса w-объектов. Вес w-объекта равен количеству объектов исходной выборки, принадлежащих клетке, т.е.:
В результате выполнения алгоритма будет получена взвешенная обучающая выборка w-объектов X .
Анализ особенностей распределения весов w-объектов, выполненный в [13], показывает, что с удалением от межклассовой границы вес большинства w-объектов экспоненциально увеличивается. Вблизи межклассовой границы большинство w-объектов имеют меньший вес. В то же время во взвешенной выборке имеется некоторое число объектов, имеющих единичный или близкий к нему вес. Анализ таких w-объектов и является способом определения выбросов по выборкам w-объектов.
Далее приведем пошаговое описание метода (рисунок 4). В результате выполнения алгоритма будет получена взвешенная обучающая выборка w-объектов.

Рисунок 4 – Построение выборки w-объектов на основе алгоритма w-GridDC
(анимация: 4 кадра, 5 циклов повторения, 130 килобайт)
4. Выводы
В ходе проведения исследований были проанализированы этапы построения обучающихся систем распознавания в целом и виды предобработки данных в частности. Было показано, что для современных интеллектуальных систем решение задач предобработки данных имеет первостепенное значение из-за большого объема и разнородности входной информации. По результатам проведенного анализа в качестве объекта исследования выбрана задача фильтрации данных, представляющая собой одну из наиболее актуальных задач Data Mining и использующаяся при решении многих прикладных задач. Выполнен анализ существующих методов определения выбросов в обучающей выборке, показавший, что наибольшее влияние на выбор шумовых объектов в силу гипотезы компактности оказывает топологическое распределение объектов обучающей выборки в пространстве признаков. Одними из наиболее эффективных алгоритмов предобработки данных, основанных на анализе взаимного расположения объектов обучающей выборки в пространстве признаков, являются алгоритмы w-baseWTS и w-GridDC построения взвешенных обучающих выборок w-объектов, поэтому разработку нового метода удаления выбросов в данных планируется выполнять на основе взвешенных обучающих выборок.
5. Список литературы
- Крисилов В.А., Юдин С.А., Олешко Д.Н. Использование гипотезы -компактности при построении обучающей выборки для прогнозирующих нейросетевых моделей // System Research & Information Technologies. – 2006. – № 3. – С. 26 – 37.
- Дуда Р., Харт П. Распознавание образов и анализ сцен. – М.: Мир, 1976. – 512 с.
- Профессиональный информационно-аналитический ресурс, посвященный машинному обучению, распознаванию образов и интеллектуальному анализу данных - Интеллектуальный анализ данных [Электронный ресурс].–Режим доступа: http://www.machinelearning.ru
- Larose D.T. Discovering knowledge in Data: An Introduction to Data Mining / D.T. Larose – New Jersey, Wiley & Sons, 2005. – 224 p.
- Pal S.K. Pattern Recognition Algorithms for Data Mining: Scalability, Knowledge Discovery and Soft Granular Computing / S.K. Pal, P. Mitra – Chapman and Hall/CRC, 2004. – 280 p.
- Загоруйко Н.Г. Методы распознавания и их применение. – М.: Сов. радио, 1972. – 208 с.
- Волченко Е.В., Кузьменко И.Ю. Анализ методов нахождения выбросов в обучающих выборках // Проблеми інформатики і моделювання. Тезиси одинадцятої міжнародної науково-технічної конференції. Секція "Молоді вчені". – Х.: НТУ "ХПІ", 2011. – С. 12 – 13.
- Дюличева Ю.Ю. О задачах фильтрации обучающих данных // Искусственный интеллект. – 2006. – № 2. – 65 – 71.
- Загоруйко Н.Г. Гипотезы компактности и -компактности в методах анализа данных // Сибирский журнал индустриальной математики. – 1998. – №1. – Том 1. – С. 114 – 126.
- Zagoruiko N.G., Borisova I.A., Dyubanov V.V., Kutnenko O.A. Methods of Recognition Based on the Function of Rival Similarity // Pattern Recognition and Image Analysis. – 2008. – Vol. 18. – №.1. – P. 1–6.
- Kohonen T. Self-Organizing Maps. – Springer-Verlag, 1995. – 501 р.
- Волченко Е.В. Сеточный подход к построению взвешенных обучающих выборок w-объектов в адаптивных системах распознавания // Вісник Національного технічного університету "Харківський політехнічний інститут". Збірник наукових праць. Тематичний випуск: Інформатика i моделювання. – Харків: НТУ "ХПІ", 2011. – № 36. – С. 12 – 22.
- Volchenko E.V. Research of features in association of training sample objects to meta-objects // 9th International Conference on “Pattern recognition and image analysis: new information technologies”: Conference Proceeding. Nizhny Novgorod, Russian Federation, 2008. – Vol. 2. – P. 291-294.
6. Важное замечание
При написании данного автореферата магистерская работа еще не завершена. Предположительная дата завершения – 10 декабря 2012г. Полный текст работы, а также материалы по теме могут быть получены у автора или его руководителя после указанной даты.
