DonNTU   Masters' portal

Abstract

Содержание

Introduction

Electroslag remelting ‒ kind of the electroslag process, electrometallurgical process, during which the metal is melted down in the bath conductive slag, heated electric shock. With this method of melting of improving the quality of metals and alloys. Electroslag remelting developed in the early 50-ies. the 20th century at the Institute of electric welding them. E. About. Paton Academy of science of Ukraine on the basis of electroslag welding. Changing the composition of the slag and the temperature mode of the process, carry out selective metal refining. As a result of electroslag remelting of sulfur content decreases in 2 ‒ 5 times, oxygen and non-metallic inclusions in 1,5 ‒ 2.5 times. The wedge is characterized by the dense aimed macrostructure, is free from defects foundry and усадочного of origin. Chemical and structural uniformity of the ingot determines the isotropy of the physical and mechanical properties of the metal.

In the Institute of electric welding named E. O. Paton in recent years, a number of technical solutions that form the basis of electroslag remelting (ESR). It is primarily a method of obtaining a hollow ingots with the use of mobile and motionless relatively ingot internal water-cooled Doorn repeated use.

1. The purpose and tasks of the work

The objective of the research is to obtain the graphic image of the process of the ESR (crystallization). For this purpose it is necessary to get acquainted with the process of electroslag remelting. Hereinafter we will consider the process of manufacture of hollow ingot.

To get the graphical image of the process of the ESR must obtain the equation of the process, which takes into account all factors affecting the process. Due to the impossibility to find out all the processes going inside the furnace was decided to review the process of the ESR on the example of the crystallization of the substance. If this were taken into account some of the parameters that have been set for the ESR.

As a result of the graphic display of the process of crystallization of substances should be set: has influence on the process of the value of the Reynolds Re or is this value can be omitted. For this it is necessary to build the surface without consideration of the given size and the surface with account of the Reynolds number.

2. Simulation of the electron beam melting

To determine the optimal thermal conditions of the formation of an ingot were calculated in the framework of the mathematical model of thermal processes in a cylindrical ingot, adapted for the case of hollow ingot (Fig. 3.1). In the model used the liquid metal into the mold of portions, and the wedge of it is pulled from time to time. The ingot surface heated by electronic beams, and the power W3 one of them is uniformly distributed in the Central zone (R2 < r < R1), and the other two, W1?2 is concentrated in the peripheral areas. In the mathematical model of the controlled process parameters are: capacity rays W1?2?3, the frequency of filling τ height at the same time the drained in the mould portions of h, the offset value of the peripheral beam from the centre on the wall of the mould (d.[3]

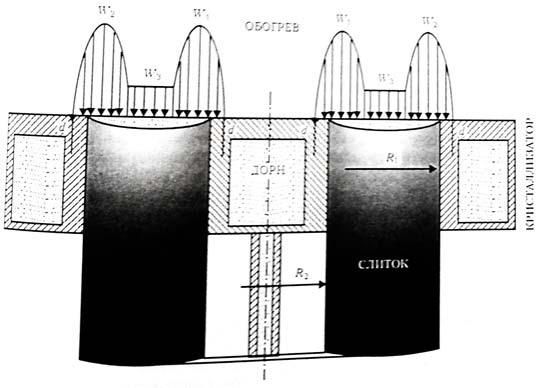
Diagram modeling of the process of formation of hollow ingot when ebric

figure 2.1 Diagram of the simulation of the process of formation of hollow ingot when ebric

The process of heat transfer is described by the equation of heat conduction in a cylindrical coordinate system (r, O, z) in the case of axial symmetry. The OZ axis of the coordinate system coincides with the axis of ingots (the axis of symmetry), and the OR ‒ with the radial direction. The origin is set at the lower the basis of the ingot.

The equation of heat conduction in this case takes the form

The equation of heat conduction

where c ‒ specific heat; ρ ‒ density; λ ‒ the heat conductivity coefficient; R1 R2 ‒ external and internal radii of ingot; s (t) ‒ the current height of the bar.

When the boundary condition on the inner surface of ingot ‒ heat exchange with the wall Dorn. Depending on that in what respect is the temperature of the surface of an ingot with some critical temperature TK (in which the surface of an ingot is separated from the the walls of the mould), heat exchange of an ingot with-mold is made to different laws.[4]

When T< TK ‒ by the law of the Stefan-Boltzmann constant

Stefan-Boltzmann Law

where ϵ ‒ the degree of blackness; σ ‒ the Stefan-Boltzmann constant; Tcρ ‒ the temperature of the walls of the mold.

When T> TK - the law of Newton-Rihman

Newton's law-Rihman

where α ‒ the coefficient of heat transfer between ingot and-mold.

The rate of melting was accepted equal to 100 kg/h, frequency of payments, as the best was chosen distribution of power electron beams in the mold, providing small liquid bath on the surface of an ingot. Such an allocation provides a uniform spreading of the flooded portions of liquid metal and practically flat crystallization front, contributing to the education of the bar of the homogeneous structure of равноосных grains.

With using the calculated mode of electron-beam heating of hollow ingot in the mold of the electron-beam installation UE-182М were melted experienced hollow ingots of titanium alloys VT1-0 with an external diameter 600 mm., internal ‒ 230 mm and a length of 2 m. The outer surface of ingots was fused electron beam.[5]

To determine the hollow titanium ingots of internal defects in the form of non-metallic inclusions, and also pores and discontinuity flaws to the method of ultrasonic flaw detection. The studies were carried out using the UD-11УА echo-pulse method in the contact version control. Operating frequency analysis was 2.5 and 5 MHz, which ensures maximum signal/noise ratio.[6]

Study of hollow ingots produced by sequential manual scan lateral surface along the generatrix of the cylinder (parallel to the longitudinal axis). The spacing between lines scan was 10...20 mm. The axis of the radiation corresponded to the radius of the cylinder. Scanning has been subjected to all of the lateral surface of the cylinder, which provide coverage of the entire volume of hollow ingot.

In the study of hollow ingots were observed multiple reflections of small amplitude, which is typical of cast metal and is the result of the reflected signal from the grain boundaries. The analysis revealed no reflections, which could be interpreted as a major non-metallic inclusions, pores and blowholes.

Thus, the inspection showed that in the investigated hollow titanium ingots there are no discontinuities, non-metallic inclusions with the size of more than 1 mm., as well as the dense clusters of smaller inclusions.

The results of the study by the method of ultrasonic were confirmed by visual research травленного fragment of hollow ingot. The structure of the ingot of a homogeneous, consisting of равноосных grain size of 10 to 30 mm.

Thus, in E.O. them. E. About. Plato for the first time in the world practice of the developed technology obtained by the method of ebric heavy wall hollow titanium ingot of a large diameter. The technology of obtaining of titanium hollow ingots method ebric and application of electron-beam melting of the surface allows to reduce metal consumption and reduce the number of technological operations.

3. Modeling of the surface crystallization process

Let Ω∈ R3 ‒ specified area, whose boundary ∂Ω consists of two closed, connected smooth surfaces Г+ Г-, not having самопересечений, with the surface of the Г± are assumed to belong to the class H(5+α) 0<α< 1. Let the next Гt (t∈ [0, T]) ‒ smooth closed surfaces, lying inside Ω such as Γ+ lies within the limitations of the field, the boundary of which is Γt. Free surface Γt ‒ the phase border in the moment of time t ‒ splits area Ω the two communication sub - Ωt-, and Ωt+, occupied by the solid and liquid phases, respectively. Required determine the velocity vector V⃗ (x, t), pressure ρ (x, t), temperature distribution of the solid and liquid phases u - (x, t) and+ (x, t) and free surface Γt on the following conditions:

the Conditions for the modeling of the process of

where Normal ‒ normal to Γt, is directed towards the Ωt+. It is assumed that the Field broken boundarythe Area of the broken boundary ‒ the area to which splits Ω the phase border Γ0 at the moment of time t=0 and Blol (x, t) ≥ ϵ0 > 0 for (x, t)∈Γlol× [0, T].

Parameters αlolKlol, K, Re,ϵ0 ‒ assumed to be positive constants and f ⃗(+) ‒ belonging to the class C2 (R1), f'⃗(+) ‒ limited in R1. The problem (1)-(6) for small values of t is solvable in a class of smooth functions, the free surface Γt belongs to the class H(2+α,(2+α)/2).

In this paper we study the influence of the Reynolds number Re in the process of crystallization of substances. In view of the complexity of the process of electroslag remelting was selected process of crystallization of the substance with the lowest minimal number of parameters.

We study the problem, modeling the process of crystallization of the substance, with the account of convective heat transfer. This task contains two free boundaries. In the paper, a graphics surfaces.

the Equation of the surface

here ρ* (φ,θ) - the equation of the free surface, at Re=0

the Equation of the surface

we Obtain the equation of the surface:

the Equation of the surface

the Coefficient Ck will find the Ritz method:

Factor Ck

Consider the zero approximation:

Zero approximation

thus we have:


Construct a system Ritz:

the System of the Ritz

and find an uncertain factor α from the equation

the uncertain factor α

this will get

the uncertain factor α

factor in the equation is the number of Re

the Equation of the surface with the number of Re

here 0 ≤ t ≤ 1 A=A(θ,φ), where "

an uncertain factor α

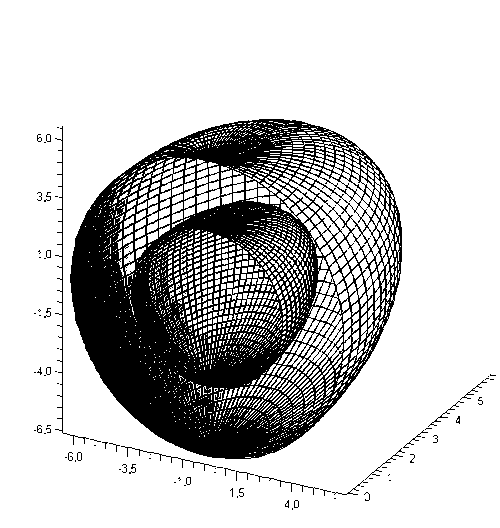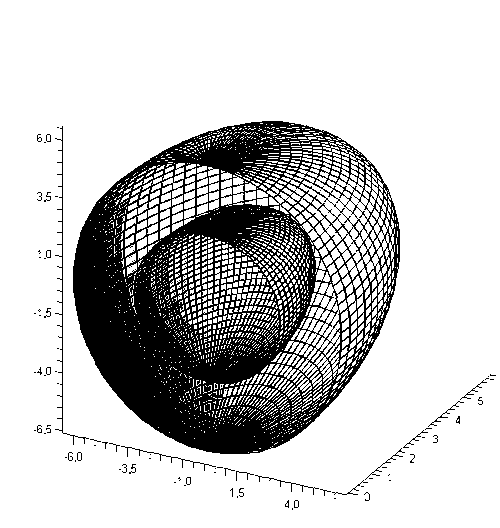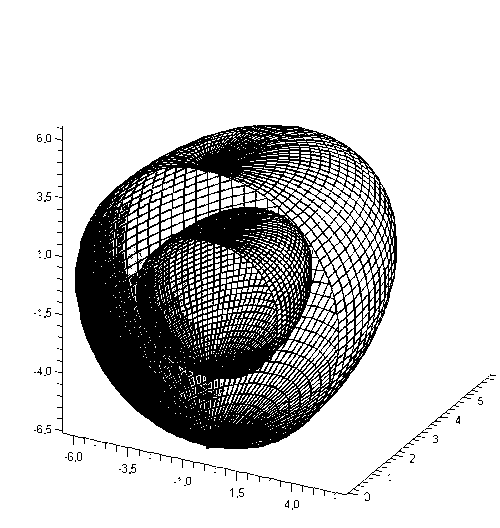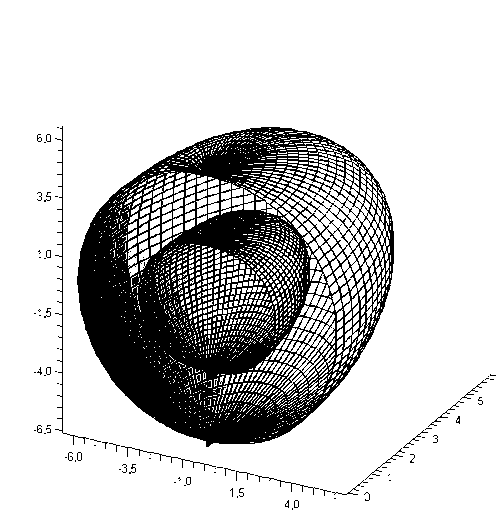
Graph surfaceρ(φ,θ) in the context of

figure 4 - the Schedule of the surfaceρ(φ,θ) in the context of

Conclusion

In the course of work were obtained equations surfaces obtained in the process of crystallization. There were received two equations, one of which was not in itself a Reynolds number and was static on the time, the second was dynamic and contained the Reynolds number.

As a result of the work was received graphics solution crystallization process. Built graphics surfaces in the space of the obtained formulas.

Comparing the graphs it can be concluded that the Reynolds number has an impact on the behavior of the process of crystallization.

References

  1. Полуфабрикаты из титановых сплавов / Н.Ф. Аношкин, М.З. Ерманюк, Г.Д. Агарков и др. ‒ М:. Металлургия, 1979. ‒ 512 с.
  2. Получение титановых труб из заготовок электронно-лучевой плавки с использованием отходов / Т.Н. Буряк, В.С. Вархушева, С.В. Ладохин и др. / / Пробл. спец. электрометаллургии. ‒ 2001. ‒ № 3. ‒ С. 24-29.
  3. Миненко А.С. Вариационные задачи со свободной границей. ‒ Киев: Наук. думка, 2005. ‒ 341 с.
  4. Солонников В.А. Разрешимость задачи о движении вязкой несжимаемой жидкости, ограниченной свободной поверхностью / / Изв. АН СССР Сер. матем. ‒ 1977. ‒ 41, № 6. ‒ С. 1388-1424.
  5. Жук Г.В., Ахонина Л.В., Тригуб Н.П. Математическое моделирование процессов кристаллизации титанового сплава Ті-64А1-4V при ЭЛПЕ / / Там же. ‒ 1998. ‒ № 2. ‒ С. 21-25
  6. Калинюк А.Н., Козловец О.Н., Ахонин С.В. Производство полуфабрикатов из титановых слитков, полученных методом электронно-лучевой плавки с промежуточной емкостью / / Пробл. спец. электрометаллургии. ‒ 2002. ‒ № 2. ‒ С. 25-28.
  7. Развитие технологии электронно-лучевой плавки титана / Б.Е. Патон, Н.П. Тригуб, В.Н. Замков, С.В. Ахонин и др. / / Пробл. спец. электрометаллургии. ‒ 2000. ‒ № 2. ‒ С. 20-25.
  8. Патон Б.Е., Тригуб Н.П., Ахонин С.В. Перспективные технологии электронно-лучевой плавки титана / / Титан. ‒ 2003. ‒ №2. ‒ С. 20-25.
  9. Ахонин С.В. Математическое моделирование процесса растворения включений TiN в расплаве титана при ЭЛП / / Пробл. спец. электрометаллургии. ‒ 2001. ‒ №1. ‒ С. 20-24.
  10. Математическое моделирование процессов рафинирования металлов от газов при электронно-лучевом переплаве с промежуточной емкостью / С.В. Ахонин, Н.П. Тригуб, А.Н. Калинюк, С.В. Цвелодуб / / Пробл. спец. электрометаллургии. ‒ 1995. ‒ №2. ‒ С. 36-42.
  11. Электронно-лучевое оплавление слитков титана / А.Н. Пикулин, Г.В. Жук, Н.П. Тригуб, С.В. Ахонин / / Современ. электрометаллургия. ‒ 2003. ‒ №4. ‒ С. 17-19.
  12. Ладыженская О.А., Солонников В.А., Уральцева Н.Н. Линейные и квазилинейные уравнения параболического типа. ‒ Москва: Наука, 1967. ‒ 756 с.