ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Електрошлаковий переплав ‒ вид електрошлакового процесу, електрометалургійний процес, при якому метал переплавляється у ванні електропровідного шлаку, нагрівається електричним струмом. При такому способі переплаву підвищується якість металів і сплавів. Електрошлаковий переплав розроблений на початку 50-х рр. 20 ст. в інституті електрозварювання ім. Е. О. Патона АН УРСР на основі електрошлакового зварювання. Змінюючи склад шлаку і температурний режим процесу, здійснюють виборче рафінування металу. В результаті електрошлакового переплаву вміст сірки знижується в 2 ‒ 5 разів, кисню і неметалевих включень в 1,5 ‒ 2,5 рази. Злиток характеризується щільною спрямованої макроструктурою, вільний від дефектів ливарного і усадочного походження.

В інституті електрозварювання імені Є. О. Патона в останні роки запропоновано ряд технічних рішень, покладених в основу електрошлакового переплаву (ЕШП). Це насамперед метод отримання порожніх злитків із застосуванням рухомих і нерухомих щодо злитку внутрішніх водоохолоджувальних дорнів багаторазового використання.

1. Мета та задачі роботи

Метою науково-дослідницької роботи є отримання графічного зображення процесу ЕШП (кристалізації). Для цієї мети необхідно познайомитися з процесом електрошлакового переплаву. Надалі будемо розглядати процес виплавки полого злитку.

Для отримання графічного зображення процесу ЕШП необхідно отримати рівняння процесу, в якому враховані всі фактори, які впливають на даний процес. Через неможливість з'ясувати всі процеси проходять всередині печі було прийнято рішення розглянути процес ЕШП на прикладі кристалізації речовини. При цьому були враховані деякі параметри, які вдалося встановити для ЕШП.

В результаті графічного відображення процесу кристалізації речовини необхідно встановити: чи надає вплив на цей процес величина Рейнольдса Re або ж цю величину можна опустити. Для цього необхідно побудувати поверхню без урахування цієї величини і поверхню з урахуванням числа Рейнольдса.

2. Процес лиття з плавленням

Схема виплавки полого злитку з нерухомим внутрішнім дорном відрізняється простотою та надійністю. Внутрішній дорн виконаний у вигляді монолітного сердечника, укладеного в охолоджувану сорочку. Під час виплавки злитку такий дорн затискається усаджувальним металом. Якщо сердечник дорна виготовити з металу з коефіцієнтом лінійного розширення більшим, ніж у металу злитку, то його нескладно отримати з відлиття шляхом спільного нагрівання і подальшого охолодження її і дорна. На малюнку 2.1 показана схема виплавки методом ЕШЛ (електрошлакового лиття) полого злитку з некрізним отвором і використанням описаного нерухомого дорна.[1]

Рисунок 2.1 - Схема виплавки методом ЕШЛ полого злитку з нескрізним отвором

Рисунок 2.1 - Схема виплавки методом ЕШЛ полого злитку з некрізним отвором:

В даний час в промисловості освоєна технологія ЕШЛ корпусів запірної енергетичної арматури з теплостійкої сталі типу 15ХІМІФ, корпусів клапанів з аустенітної сталі типу 18-8, частин корпусів судин високого тиску.[2]

Безсумнівний інтерес представляє отримання виробів складної форми сполученням ЕШЛ із електрошлакового зварювання. Для цього деякі частини майбутнього виробу встановлюють в кристалізаторі таким чином, щоб під час відлиття основної частини виробу вони приплавились до неї.

2.1 Процес лиття з приплавленням

Технологія лиття з одночасним приплавленням заздалегідь підготовлених частин виробу можлива лише на основі електрошлакового процесу. Приплавляємі щоки до відлиття встановлені в отвори кристалізатора шийки майбутнього валу.

За аналогічною схемою виготовляється кривошип колінчатого вала. Під час виплавки шийки раніше виплавленні щоки приплавляються до неї.

Технологія ЕШЛ має велике прикладне значення, оскільки дозволяє ефективно вирішувати проблему зниження великих виробів складної форми, які раніше одержувала з поковок.

Наявне обладнання і технологія дозволяють нашій промисловості отримувати методом ЕШЛ литі заготовки таких виробів відповідального призначення, як колінчаті вали й шатуни великих дизелів морських суден, корпусу енергетичної арматури і судин високого тиску, порожнисті злитки, валки холодної прокатки, гребні вали, заготівлі роторів турбін і турбогенераторів, вали каландр та ін.

3. Моделювання процесу ЭЛПЕ

Для визначення оптимальних теплофізичних умов формування злитку були проведені розрахунки в рамках математичної моделі теплових процесів в циліндричному злитку, адаптованої для випадку полого злитку (мал. 3.1). У цієї моделі рідкий метал зливається в кристалізатор порціями, а злиток з його витягується періодично. Поверхня злитку обігрівається електронними променями, причому потужність W3 одного з них рівномірно розподілена в центральній зоні (R2 < r < R1), а двох інших W1 і W2 сконцентрована в периферійних зонах. У математичної моделі контрольованими технологічними параметрами є: потужності променів W1, W2 і W3, періодичність заливки τ, висота одночасно охолоджувальних в кристалізатор порції h, величина переміщення периферійного променя від центру на стінку кристалізатора d.[3]

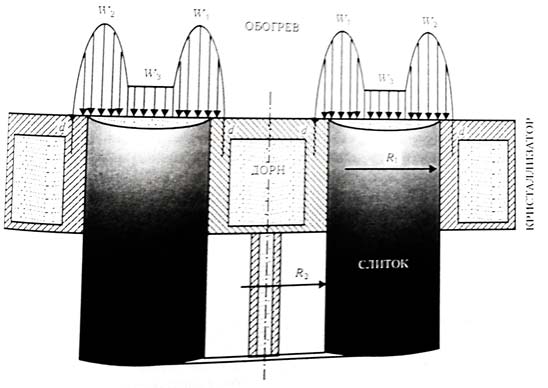
Схема моделювання процесу формування полого злитку при ЭЛПЕ

Рисунок 2.1 - Схема моделювання процесу формування полого злитку при ЭЛПЕ

Процес переносу тепла описується рівнянням теплопровідності в циліндричної системі координат (r, O, z) для випадку осьовий симетрії. Вісь OZ системи координат збігається з віссю злитку (вісь симетрії), а вісь OR ‒ з радіальним напрямом. Початок координат задано на нижній підставі злитку.

Рівняння теплопровідності в цьому випадку приймає вигляд

Рівняння теплопровідності

де c ‒ питома теплоємність; ρ ‒ щільність; λ ‒ коефіцієнт теплопровідності; R1 і R2 ‒ зовнішній і внутрішній радіуси злитку; s (t) ‒ поточна висота злитку.

При цьому граничне умова на внутрішній поверхні злитку ‒ теплообмін зі стінкою дорна. Залежно від того, в якому щодо знаходиться температура поверхні злитку з деякою критичною температурою TK (при якій поверхню злитку відділяється від стінки кристалізатора), теплообмін злитку з кристалізатором здійснюється за різними законами.[4]

При T< TK ‒ за законом Стефана-Больцмана

Закон Стефана-Больцмана

де ϵ ‒ ступінь чорноти; σ ‒ постійна Стефана-Больцмана; Tcρ ‒ температура стінки кристалізатора.

При T> TK - за законом Ньютона-Рихмана

Закон Ньютона-Рихмана

де α ‒ коефіцієнт теплопередачі між злитком і кристалізатором.

Швидкість плавки була прийнята рівною 100 кг/год, періодичність розрахунків в якості оптимального було обрано розподіл потужності електронних променів в кристалізаторі, забезпечує дрібну рідку ванну на всій поверхні злитку. Такий розподіл забезпечує рівномірне розтікання заливаються порцій рідкого металу і практично плоский фронт кристалізації, який сприяє утворенню в злитку гомогенної структури з рівноосьових зерен.

З використанням розрахованого режиму електронно-променевого нагріву полого злитку в кристалізаторі на електронно-променевої установки УЕ-182 М були виплавлені досвідчені порожнисті злитки титанового сплаву ВТ1-0 з зовнішнім діаметром 600 мм., внутрішнім ‒ 230 мм. та довжиною 2 м. Зовнішня поверхня злитків була оплавлена електронним променем.[5]

Для визначення в порожніх титанових злитках внутрішніх дефектів у вигляді неметалічних включень, а також повітряних пір застосовувався методу ультразвукової дефектоскопії. Дослідження проводилися з використанням приладу УД-11УА эхо-імпульсним методом при контактному варіанті контролю. Робоча частота аналізу становила 2,5 і 5 МГц, що забезпечувало максимальне співвідношення сигнал/шум.[6]

Дослідження порожніх злитків вироблялося шляхом послідовного ручного сканування бічній поверхні уздовж утворює циліндру (паралельно поздовжньої осі). Крок між лініями сканування дорівнював 10...20 мм. Вісь випромінювання відповідала радіусу циліндра. Сканування піддавалася вся бічна поверхня циліндра, що забезпечувало охоплення всього обсягу полого злитку.

При дослідженні порожніх злитків спостерігалися множинні відображення малої амплітуди, що типово для литого металу і є результатом відображення сигналу від границь зерен. Аналізом не виявлено відбиттів, які можна було б інтерпретувати як великі неметалічні включення, пори, усадочні раковини.

Таким чином, УЗК показав, що в досліджених порожніх титанових злитках відсутні звані неоднорідності, неметалічні включення з розміром більше 1 мм., а також щільні скупчення дрібних включень.

Результати дослідження методом УЗК були підтверджені візуальними дослідженнями травлення фрагмента полого злитку. Структура злитку однорідна, що складається з рівноосьових зерен розміром 10...30 мм.

Таким чином, у ІЕЗ ім. Е. О. Платона вперше в світовій практиці за розробленою технологією отриманий методом ЭЛПЕ товстостінний порожнистий титановий злиток великого діаметра. Технологія отримання титанових порожніх злитків методом ЭЛПЕ і застосування електронно-променевого оплавлення їх поверхні дозволяє значно знизити витрати металу і скоротити кількість технологічних операцій.

4. Моделювання поверхні процесу кристалізації

Нехай Ω∈ R3 ‒ задана область, кордон якої ∂Ω складається з двох замкнутих, зв'язних гладких поверхонь Р+ і-, не мають самоперетину, причому поверхні Р± передбачаються що належать класу H(5+α), 0<α< 1. Нехай далі Рt (t∈ [0, T]) ‒ гладкі замкнуті поверхні, що лежать в Ω, такі, що Γ+ лежить всередині обмежень області, кордоном якої є Γt. Вільна поверхня Γt ‒ кордон розділу фаз в момент часу t ‒ розбиває область Ω на дві зв'язні під області Ωt- Ωt+, займаних твердого та рідкого фазами відповідно. Потрібно визначити вектор швидкості V⃗ (x, t), тиск ρ (x, t), розподілу температур твердої та рідкої фаз u - (x, t) і u+ (x, t) і вільну поверхню Γ за наступними умовами:

Умови для моделювання процесу

де Нормально ‒ нормаль до Γt, спрямована в бік Ωt+. Передбачається, що Області розбиті кордономОбласть розбита кордоном ‒ області, на які розбиває Ω кордон розділу фаз Γ0 у момент часу t=0 і B± (x, t) ≥ ϵ0 > 0 при (x, t)∈Γ±× [0, T].

Параметри α±, K±, K, Re,ϵ0 ‒ вважаються позитивними постійними, а f ⃗(u+) ‒ належить класу C2 (R1), f'⃗(u+) ‒ обмеженою в R1. Завдання (1)-(6) при малих значеннях t розв'язана в класі гладких функцій, при цьому , а вільна поверхня Γt належить до класу H(2+α,(2+α)/2).

В даній роботі досліджується вплив числа Рейнольдса Re на процес кристалізації речовини. В увазі складності процесу електрошлакового переплаву був обраний процес кристалізації речовини з мінімальним відомим кількістю параметрів.

Вивчається завдання, моделююча процес кристалізації речовини, з урахуванням конвективного переносу тепла. При цьому завдання містить дві вільних кордона. У роботі побудовані графіки поверхонь.

Рівняння поверхні

тут ρ* (φ,θ) - рівняння вільної поверхні, при Re=0

Рівняння поверхні

Одержимо рівняння поверхні:

Рівняння поверхні

Коефіцієнт Ck знайдемо методом Рітца:

Коефіцієнт Ck

Розглянемо нульові наближення:

Нульові наближення

Таким чином отримаємо:


Побудуємо систему Рітца:

Система Рітца

і знайдемо невизначений коефіцієнт α з рівняння

невідомий коефіцієнт α

звідси отримаємо

невідомий коефіцієнт α

Включимо в рівняння число Re

Рівняння поверхні з числом Re

тут 0 ≤ t ≤ 1 A=A(θ,φ), де

невизначений коефіцієнт α

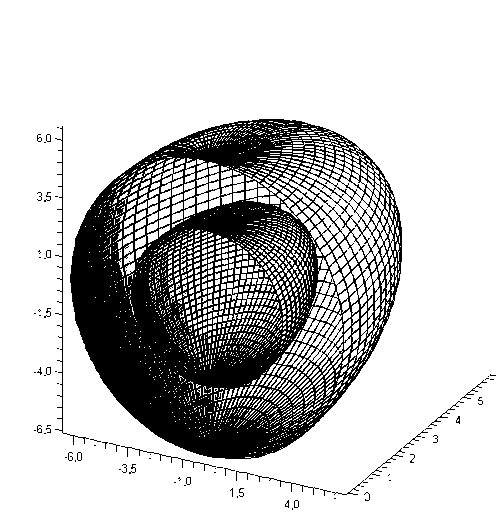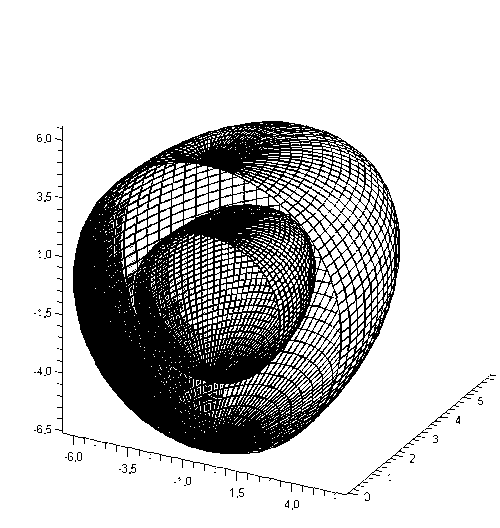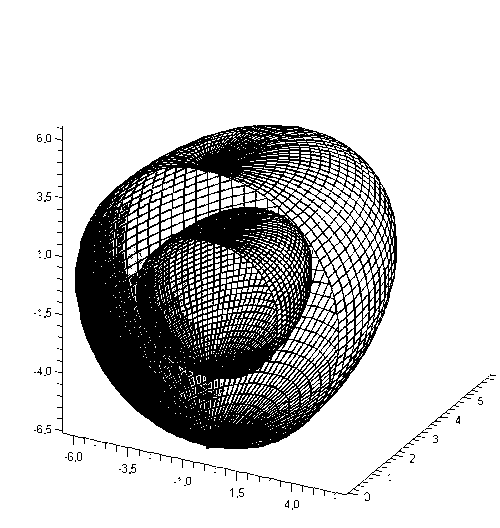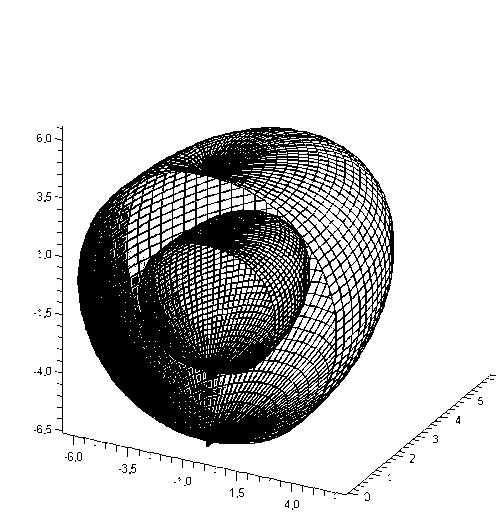
Графік поверхніρ(φ,θ) в розрізі

Рисунок 4 - Графік поверхні ρ(φ,θ) у розрізі

Висновки

В ході виконання роботи було отримано рівняння поверхонь одержуваних у процесі кристалізації. Були отримані два рівняння, одне з яких не мала в собі числа Рейнольдса і була статично щодо часу, друге було динамічно і містило числа Рейнольдса.

В результаті виконання роботи було отримано графічне рішення процесу кристалізації. Побудовані графіки поверхонь в просторі по отриманих формулами.

Порівнюючи графіки можна зробити висновок, що число Рейнольдса впливає на поведінку процесу кристалізації.

Перелік посилань

  1. Полуфабрикаты из титановых сплавов / Н.Ф. Аношкин, М.З. Ерманюк, Г.Д. Агарков и др. ‒ М:. Металлургия, 1979. ‒ 512 с.
  2. Получение титановых труб из заготовок электронно-лучевой плавки с использованием отходов / Т.Н. Буряк, В.С. Вархушева, С.В. Ладохин и др. / / Пробл. спец. электрометаллургии. ‒ 2001. ‒ № 3. ‒ С. 24-29.
  3. Миненко А.С. Вариационные задачи со свободной границей. ‒ Киев: Наук. думка, 2005. ‒ 341 с.
  4. Солонников В.А. Разрешимость задачи о движении вязкой несжимаемой жидкости, ограниченной свободной поверхностью / / Изв. АН СССР Сер. матем. ‒ 1977. ‒ 41, № 6. ‒ С. 1388-1424.
  5. Жук Г.В., Ахонина Л.В., Тригуб Н.П. Математическое моделирование процессов кристаллизации титанового сплава Ті-64А1-4V при ЭЛПЕ / / Там же. ‒ 1998. ‒ № 2. ‒ С. 21-25
  6. Калинюк А.Н., Козловец О.Н., Ахонин С.В. Производство полуфабрикатов из титановых слитков, полученных методом электронно-лучевой плавки с промежуточной емкостью / / Пробл. спец. электрометаллургии. ‒ 2002. ‒ № 2. ‒ С. 25-28.
  7. Развитие технологии электронно-лучевой плавки титана / Б.Е. Патон, Н.П. Тригуб, В.Н. Замков, С.В. Ахонин и др. / / Пробл. спец. электрометаллургии. ‒ 2000. ‒ № 2. ‒ С. 20-25.
  8. Патон Б.Е., Тригуб Н.П., Ахонин С.В. Перспективные технологии электронно-лучевой плавки титана / / Титан. ‒ 2003. ‒ №2. ‒ С. 20-25.
  9. Ахонин С.В. Математическое моделирование процесса растворения включений TiN в расплаве титана при ЭЛП / / Пробл. спец. электрометаллургии. ‒ 2001. ‒ №1. ‒ С. 20-24.
  10. Математическое моделирование процессов рафинирования металлов от газов при электронно-лучевом переплаве с промежуточной емкостью / С.В. Ахонин, Н.П. Тригуб, А.Н. Калинюк, С.В. Цвелодуб / / Пробл. спец. электрометаллургии. ‒ 1995. ‒ №2. ‒ С. 36-42.
  11. Электронно-лучевое оплавление слитков титана / А.Н. Пикулин, Г.В. Жук, Н.П. Тригуб, С.В. Ахонин / / Современ. электрометаллургия. ‒ 2003. ‒ №4. ‒ С. 17-19.
  12. Ладыженская О.А., Солонников В.А., Уральцева Н.Н. Линейные и квазилинейные уравнения параболического типа. ‒ Москва: Наука, 1967. ‒ 756 с.