Векторизация растровых изображений
Автор: Д.Гелецян
Источник: http://it-claim.ru/Library/Books/ITS/wwwbook/3_sb/geletcyan.htm
Автор: Д.Гелецян
Источник: http://it-claim.ru/Library/Books/ITS/wwwbook/3_sb/geletcyan.htm
Д.Гелецян Векторизация растровых изображений. Разрешение прблемы перевода растровых изображений в векторный формат при построении систем распознавания графических образов. Рассматривается алгоритм векторизации растровых изображений.
При анализе и обработке растровых изображений часто возникает необходимость работать с изображением не как с массивом точек, а как с набором команд, описывающих это изображение (например, чертежи, карты и т. д.). Проблема перевода растровых изображений в векторный формат возникает также при построении систем распознавания графических образов. В самом простом случае это можно проиллюстрировать следующим примером: дан массив точек (растровое изображение), на котором предположительно есть некоторый треугольник. Необходимо проверить наличие данного объекта в этом массиве. Задача, согласитесь, намного упростится, если то же изображение будет задано тремя командами line: line(x1_i, y1_i, x2_i, y2_i), i=1, 2, 3.
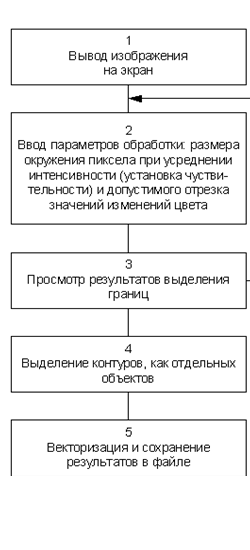
В данной статье рассматривается алгоритм векторизации растровых изображений (256 цветов; градации серого – GrayScale). Изображение может содержать полутоновые переходы и элементы с расплывчатыми границами. Процесс векторизации можно условно представить в виде последовательности пяти этапов (рис. 1).
Рассмотрим эти этапы более подробно. В дальнейших рассуждениях некоторые понятия заключаются в кавычки из-за условности их применения в изложении обобщенных принципов работ алгоритмов.
Растровое изображение (с палитрой из 256-ти цветов) строится приблизительно следующим образом: элементы массива размером X_size*Y_size*sizeof(char)= X_size*Y_size байт после распаковки графических данных из файла содержат номера цветов в палитре. Каждый элемент массива лежит в пределе [0, 255] и соответствует одному пикселю.
В палитре хранятся R-, G- и B- составляющие цветов, используемых в изображении. N-му номеру цвета соответствует N-ая тройка байтов в палитре.
Для дальнейших рассуждений примем некоторые соглашения по формату входных данных:
Используются изображения с палитрой (256 цветов) GrayScale (градации серого). Это подразумевает: что R-, G- и B – составляющие цветов в палитре равны; каждой составляющей отводится по 1 байту, то есть значение каждой составляющей цвета в палитре изменяется в пределах [0,255]; первая тройка байтов в палитре соответствует черному цвету, последняя – белому; в палитре цвет «плавно» изменяется от черного к белому. Получаем палитру следующего вида:
00h 00h 00h 01h 01h 01h 02h 02h 02h 03h 03h 03h........feh feh feh ffh ffh ffh (всего: 256*3*1=768 байт).
Эти условия выполняются при конвертировании в формат GrayScale(8 бит) большинством конвертеров, например, конвертером, включенным в MS Photo Editor.
Итак, после распаковки растрового файла создается массив размером X_size*Y_size*sizeof(char)= X_size*Y_size, содержащий номера цветов из палитры ([0. 255]).
Для неточной обработки с целью упрощения вычислений интенсивность можно округлять до ближайшего целого числа, кратного 16. Но этот частный случай здесь не рассматривается.
Если до этого подразумевались целочисленные величины (номера цветов), то теперь переходим к использованию дробных чисел для описания пикселей. Мы можем сделать это, поскольку при равномерном изменении цветов в палитре нас уже не интересуют сами номера цветов в палитре. Нам, например, достаточно знать, что пиксель, которому поставлено в соответствие число 55.5, «светлее» пикселя, которому соответствует число 55.0, и «темнее» пикселя, которому соответствует число 56.0. Дальше в рассуждениях термины «цвет» и «интенсивность» можно считать равноценными.
В целях устранения мелких неровностей (шумов) в изображении и установки нужной при анализе чувствительности проводится усреднение цвета: замена цвета пикселя средним цветом его окружения.
Для каждой строки изображения перебираются пиксели, и для каждого пикселя вычисляется и запоминается, например, в одномерном массиве среднее значение цвета в квадрате вокруг него (рис. 2). Размер квадрата является одним из входных параметров при выделении границ. Чем больше квадрат, тем меньше чувствительность к маленьким элементам (дефектам) изображения и тем меньше колебания в цвете от пикселя к пикселю. (В программной реализации этот параметр мог находиться на отрезке [1, 6]).
Итак, для i-ой строки мы уже имеем одномерный массив, в котором номер элемента является номером пикселя в строке, а значением элемента является средний цвет его окружения. В этом массиве выделяем участки возрастания и убывания интенсивности (рис. 3). Возрастание или убывание не обязательно должны быть строгими: допускается содержание в них некоторых «небольших» участков с нулевым (или даже с «небольшим» обратным) изменением интенсивности. Также следует отметить тот факт, что участки монотонности могут быть «достаточно длинными», поэтому необходимо ограничивать максимальную длину участков.
Теперь для выделенного участка каждому пикселю ставим в соответствие разницу в цвете между ним и следующим за ним пикселем. Назовем эту разницу весом; чем больше разница в интенсивности между соседними пикселями, тем больший вес (или значение) имеет пиксель.

Теперь рассмотрим сам процесс векторизации.
На входе мы имеем два массива координат (x(n), y(n)) точек на контуре. Задача состоит в том, чтобы заменить их дугами и отрезками прямых.
Для начала отметим, что, так как здесь используются интерполированные значения координат, то случайные ошибки (неровности, угловатости и т. д.) исключены, поэтому для упрощенного учета ошибок достаточно просто установить порог (максимальное расстояние от точки дуги или прямой до точки контура, при котором мы считаем их совпадающими). Подобный подход дает вполне удовлетворительные результаты.
Радиус кривизны в точке можно вычислить по второй производной ( «Краткий курс по математическому анализу» Пискунов С.), и далее проводить дугу с вычисленным радиусом до тех пор, пока приближение дугой остается в заданных пределах. Однако, подобный способ очень чувствителен к погрешностям, тем более, что мы имеем дело с дискретными значениями координат.
Процесс векторизации удобнее провести непосредственным сравнением дуг и прямых с координатами точек контуров. Алгоритм выглядит следующим образом:
начальная_точка = Начальная точка.
конечная_точка = Конечная точка.
Конечная_точка, средняя_точка и начальная_точка лежат на одной прямой?
Да. Координаты точек между ними лежат на одной прямой (с заданной точностью)?
Да. Между ними прямая. Запомнить ее.
Начальная_точка=конечная_точка.
Конечная_точка=конечная точка.
Начать сравнение сначала с новыми переменными.
Нет. конечная_точка= конечная_точка - шаг. Продолжить сравнение.
Нет. Координаты точек между ними лежат на дуге (с заданной точностью)?
Да. Между ними дуга. Запомнить ее.
Начальная_точка= конечная_точка.
Конечная_точка=конечная точка.
Начать сравнение сначала с новыми переменными.
Нет. конечная_точка= конечная_точка - шаг. Продолжить сравнение.
Необходимо
рассмотреть некоторые частные случаи,
например, случай, при котором начальная и конечная точки оказываются в
«непосредственной
близости» друг от друга (в пространстве XY), и как следствие мы имеем большие погрешности
при вычислении
радиуса и центра окружности. Здесь просто можно временно взять другие
точки.В понятие «точка» мы вкладываем усредненное
значение ее окружения.
Приведенные здесь алгоритмы были реализованы
программно в среде Borland C++
5.01. При этом, были выбраны следующие форматы данных: формат входных
данных –PCX, выходных –DXF. Программа называется RASP, занимает
![]() 100 КВ
дискового пространства.
100 КВ
дискового пространства.
В результате проведенных вычислений и исследований была предложена схема векторизации растровых изображений. Были предложены несколько методов решения задач, возникших при разработке алгоритма. Были даны предварительные оценки этим методам, были отмечены их преимущества и недостатки.