Реферат по теме выпускной работы
Содержание
- Введение
- 1. Исследование асинхронного режима
- 2. Меры для повышения динамической устойчивости
- 3. Математическое моделирование динамических режимов синхронного генератора
- Выводы
- Список источников
Введение
Обеспечение динамической устойчивости синхронных генераторов в аварийных режимах является одной из наиболее актуальных задач управления современными электрическими станциями и системами. То обстоятельство, что система сохраняет статическую устойчивость в установившемся режиме работы, еще не позволяет утверждать, что она окажется устойчивой и при резких внезапных нарушениях режима ее работы, подобных короткому замыканию, отключения генераторов или линий и прочее [1].
При переходе генератора в асинхронный режим по мере снижения магнитного потока, создаваемого этим током в обмотке ротора, генератор начинает потреблять реактивную мощность из сети.
Равновесие между уменьшающимся до нуля синхронным электромагнитным моментом и крутящим моментом турбины нарушается, и частота вращения генератора начинает превышать синхронную. Под влиянием магнитного поля тока статора, в зубцах и клиньях ротора и в его обмотке, если она остается замкнутой на возбудитель или замкнется на резистор самосинхронизации, появятся токи с частотой скольжения. Магнитный поток от этих токов, взаимодействуя с магнитным полем статора, создает тормозящий асинхронный момент, что обеспечивает выдачу генератором активной мощности в сеть при асинхронном режиме. Асинхронный тормозящий момент с увеличением скольжения ротора возрастает. Когда он станет равным вращающему моменту турбины, дальнейшее повышение скольжения прекратится. Наступит устойчивый асинхронный режим.
Реагируя на увеличение частоты вращения, регулятор частоты вращения турбины сокращает поступления пара (воды) и тем самым уменьшает активную мощность. Токи, появляющиеся в зубцах, клиньях и бочке ротора, при асинхронном режиме турбогенератора вызывают нагрев ротора. При повышенном скольжении ток статора может значительно превышать номинальное значение, может привести к перегреву обмотки статора. Из-за роста результирующей магнитной индукции в торцевых областях турбогенератора при потере возбуждения увеличивается подогрев крайних пакетов стали и конструктивных элементов торцевых зон статора.
В асинхронном режиме в обмотке ротора наводится напряжение. Если обмотка изолирована или включена не в электромашинный возбудитель, а на систему выпрямителей возбуждения, исключает прохождение тока обратной полярности, то при больших скольжениях подведенное напряжение может достичь опасного для обмотки ротора и выпрямителей значение. Поэтому асинхронный режим очень опасен для генераторов [3].
Целью работы является исследование асинхронных режимов электрических станций и разработка средств по повышению динамической устойчивости.
Исходными данными для выполнения работы являются:
- Справочные данные мгновенных значений токов, напряжений, скоростей турбогенератора и др., полученных путём цифрового осциллографирования.
- Параметры электроэнергетической системы (ЭЭС), на основе которых рассчитаны эквивалентные ЭДС E, сопротивления R, емкости C, индуктивности L [4].
Основные задачи разработок и исследований:
- доказать необходимость избегания асинхронного режима;
- выявление асинхронных режимов на раннем этапе;
- усовершенствовать дискретную математическую модель для анализа динамических режимов электрической системы, на основе которой создана программа PowerNet;
- предложить новый принцип защиты от асинхронных режимов.
1. Исследование асинхронного режима
Рассмотрим метод контроля угла вылета ротора (в реальных условиях трудно измерить данный угол). Для этого выполним моделирование возбужденного асинхронного режима генератора при близком коротком замыкании (КЗ) [6].
Перед рассмотрением аварийного режима определим зависимость устойчивости от угла вылета ротора. В режиме работы в точке а (рис. 1) мощности генератора и турбины уравновешивают друг друга. Если предположить, что угол δa получает небольшой прирост Δδ , то мощность генератора, придерживаясь синусоидальной зависимости от угла, также изменится на определенную величину ΔР, причем, как видно из рис.1 в точке а положительному приросту угла Δδ соответствует также положительное изменение мощности генератора ΔР .
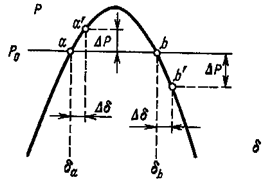
Рисунок 1 – Изменение мощности при увеличении угла
Что касается мощности турбины, то она не зависит от угла δ и при любых изменениях последнего остается постоянной и равной Рo. В результате изменения равновесие моментов турбины и генератора оказывается нарушенной и на валу машины возникает чрезмерный момент тормозного характера, поскольку тормозной момент генератора за счет положительного изменения мощности ΔР преобладает над крутящим моментом турбины.
Под влиянием тормозного момента ротор генератора начинает замедляться, что обусловливает перемещение связанного с ротором вектора Э.Д.С. генератора в сторону уменьшения угла δ. В результате уменьшения угла вновь восстанавливается исходный режим работы в точке а, следовательно, этот режим должен быть признан устойчивым. К тому же выводу можно прийти и при отрицательном приросте угла Δδ в точке а.
Совсем другая картина получается в точке b. Здесь положительный прирост угла Δδ сопровождается не положительной, а отрицательной изменением мощности генератора δР. Изменение мощности генератора вызывает появление избыточного момента ускоряющего характера, под влиянием которого угол не уменьшается, а растет. С увеличением угла мощность генератора продолжает падать, что обусловливает дальнейшее увеличение угла и т. д. Процесс сопровождается непрерывным перемещением вектора ЭДС Е относительно вектора напряжения приемной системы U и станция выпадает из синхронизма.
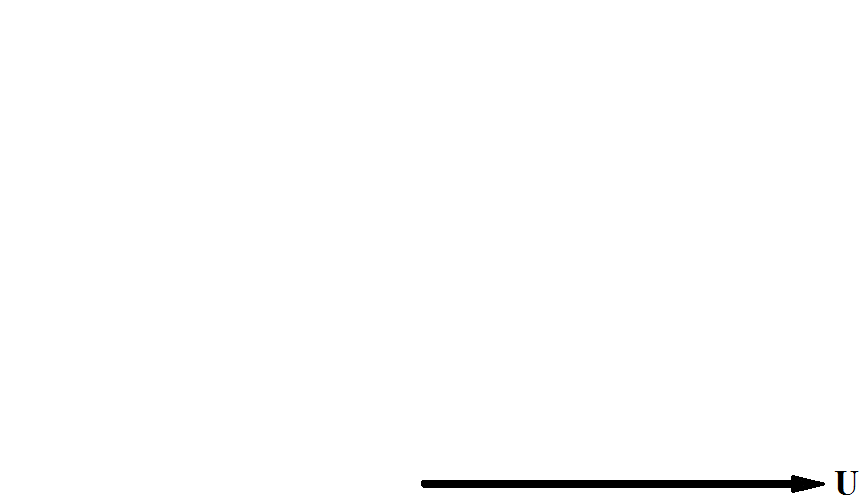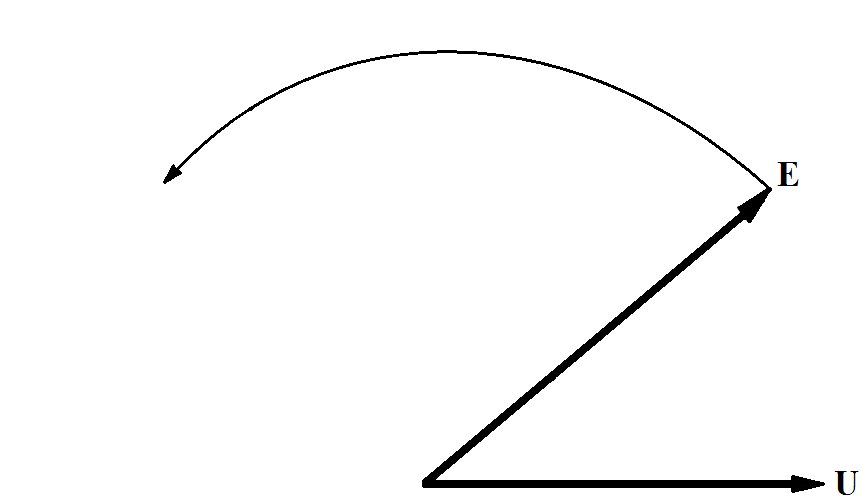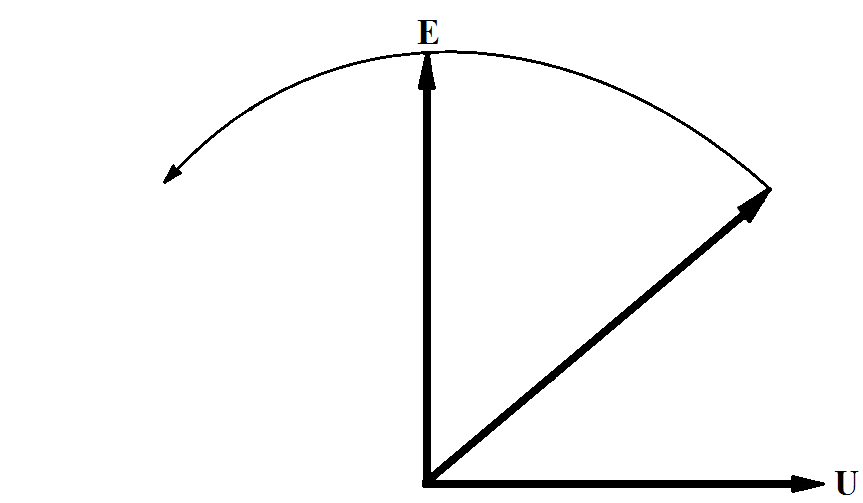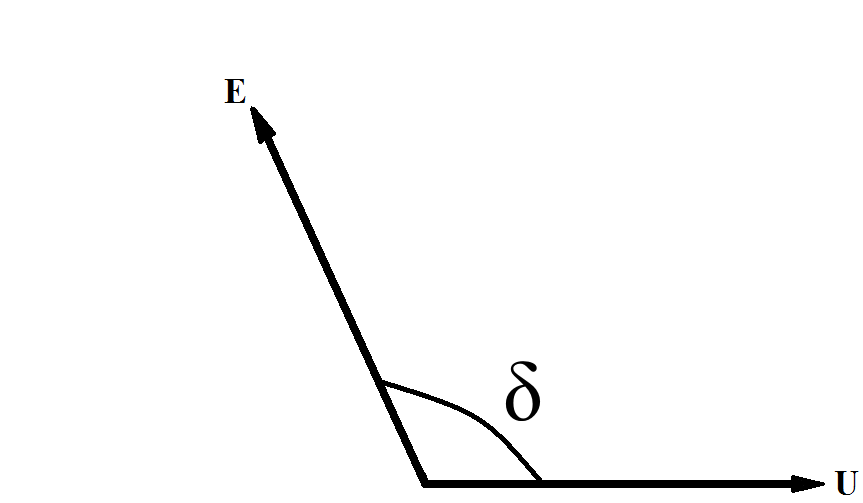
Рисунок 2 – Выпадение из синхронизма
Таким образом, режим работы в точке b статически неустойчив и практически неосуществим.
На рис. 3 представлена схема блочной ТЭС. Моделируется переходный режим при коротком замыкании на стороне высшего напряжения (ОРУ 110 кВ) с последующим его отключением [5].
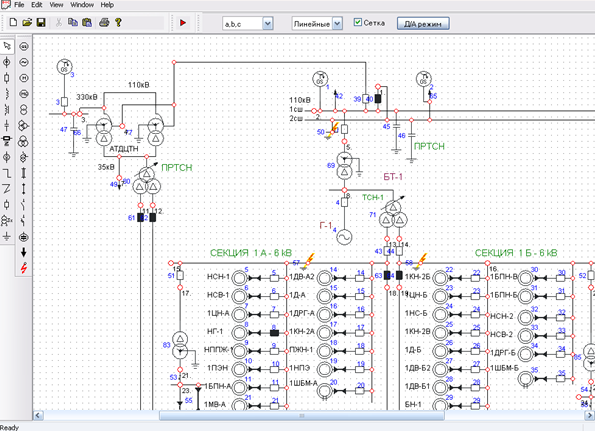
Рисунок 3 – Фрагмент схемы блочной ТЕС
Наблюдаем процесс отключения короткого замыкания за время отключения 0,5 с.
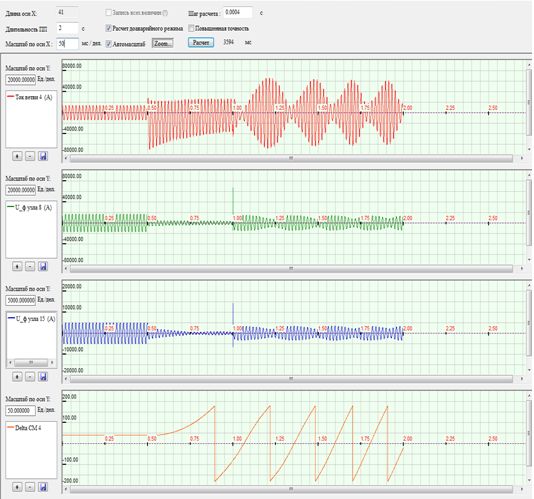
Рисунок 4 – Осциллограмма переходного процесса отключения короткого замыкания через 0,5 с: а) ток генератора (ветвь № 4); б) напряжение узла № 8; в) напряжение узла № 15; г) угол вылета ротора.
Показано четыре осциллограммы. На первой осциллограмме показан ток ветви № 4 (генератор), на второй осциллограмме напряжение узла № 8, третья осциллограмма - напряжение узла 15 и на четвертой осциллограмме угол вылета ротора Delta. За время К.З. Delta растет и после отключения наступает стойкий или возбужденный асинхронный режим.
На рисунке 5 показан переходный процесс отключения КЗ через 0,25 с.
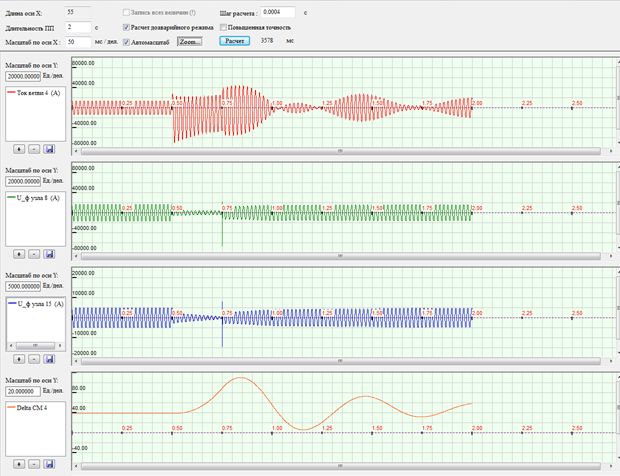
Рисунок 5 – Осциллограмма переходного процесса отключения короткого замыкания через 0,25 с.
Как видно из осциллограммы, угол вылета ротора за это время не успевает превысить критическую величину (90°), и после отключения КЗ происходит втягивание генератора в синхронизм, сопровождающееся «колебаниями» ротора.
2. Меры для повышения динамической устойчивости
Динамическая устойчивость энергосистемы характеризует способность системы сохранять синхронизм после внезапных и резких изменений параметров режима или при авариях в системе (коротких замыканиях, отключений часта генераторов, линий или трансформаторов). После таких внезапных нарушений нормальной работы в системе возникает переходный процесс, по окончании которого вновь должен наступить установившийся послеаварийный режим работы [2].
Существуют несколько способов повышения устойчивости:
- Контроль изменения обобщенного вектора тока на основе его дифференцирования по времени.
- Контроль изменения частоты по времени на основе решения нелинейных систем уравнений.
- По углу из векторной диаграммы на основе контроля величины сопротивления Z, рассчитанного по мгновенным значениям обобщенного тока.
Рассмотрим подробно метод контроля изменения обобщенного вектора тока на основе его дифференцирования по времени при близких КЗ.
Повышение устойчивости станции при близких повреждениях возможно за счет применения новых принципов построения микропроцессорных защит. Этот принцип заключается в создании быстродействующего токовой защиты, который выполняет анализ мгновенных значений обобщенного вектора тока (ОВТ) и его первой производной по времени, так как именно производная ОВТ имеет значительную разницу в режиме КЗ и при качаниях.
Принцип на основе контроля величины первой производной ОВТ позволяет существенно повысить быстродействие защиты по сравнению с существующими за счет более точной идентификации режима на ранней стадии, так как существующие системы, как правило, реагируют на действующие значения, что может привести к задержке срабатывания, в течение которой угол вылета ротора генератора достигнет критического значения.
3. Математическое моделирование динамических режимов синхронного генератора
Для того, чтобы доказать перспективы построения МП–защиты на основе мгновенных значений ОВТ и выбора ее информативных параметров выполним компьютерное моделирование аварийных режимов, сопровождающихся нарушением динамической устойчивости.
Расчет мгновенных значений токов, напряжений и электромеханических величин в переходном процессе выполним с помощью программы PowerNet, разработанной на основе дискретных математических моделей [8].
Рассмотрим случай возникновения асинхронного хода.
Расчетная схема создана на основе данных блока 200 МВт. Генератор ТГВ-200 оборудован тиристорной системой самовозбуждения с АРЗ пропорционального действия и форсированием. Автотрансформаторная связь отключена [9].
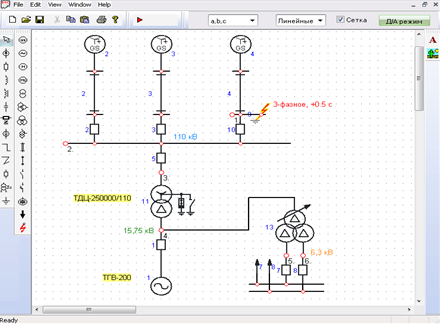
Рисунок 6 – Расчётная схема блока 200 МВт для анализа асинхронного режима
Проведем анализ следующего режима:
- 0 – нормальный режим;
- 0,5 с. – возникновение 3-фазного КЗ на шинах ОРУ 110 кВ;
- 1,0 с. – отключение КЗ релейной защитой.
На рисунке 7 представлены осциллограммы переходного процесса, полученные с помощью моделирования. На 1-м графике – ток в генераторе, на 2-м – напряжение на выводах генератора (фаза А), на 3-м - крутящий момент на валу генератора (и.о.), на нижнем - относительная угловая скорость турбоагрегата.
Размер ударного тока КЗ в данном режиме – 80 кА. После 1 с от начала отсчета повреждения был отключен, после чего пошли качания ротора (видно из графика 3), и далее, произошел выход генератора из синхронизма с системой. Данный режим сопровождался битьем тока с достаточно большой амплитудой (до 70 кА).
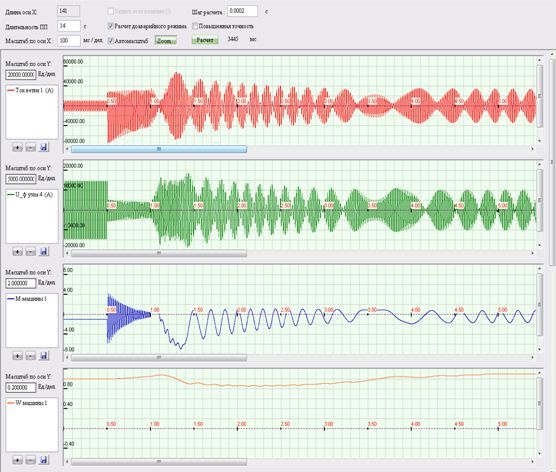
Рисунок 7 – Расчетные осциллограммы асинхронного хода генератора при отключении КЗ через 0,5 с (масштаб времени 100 мс / дел)
Выполним анализ поведения генератора при использовании быстродействующей защиты на основе измерения мгновенных значений ОВТ и его производной, позволяет отключить КЗ через 0,1 с.
ОВТ находим как:
где ia, ib ,ic – соответственно токи в фазах А, В, С [7].
Далее необходимо найти его первую производную по времени путем численного дифференцирования (используется формула второго порядка).
Производная ОВТ в режиме КЗ имеет значительное изменение, а при качаниях – нет, потому эта защита реагирует только на КЗ.
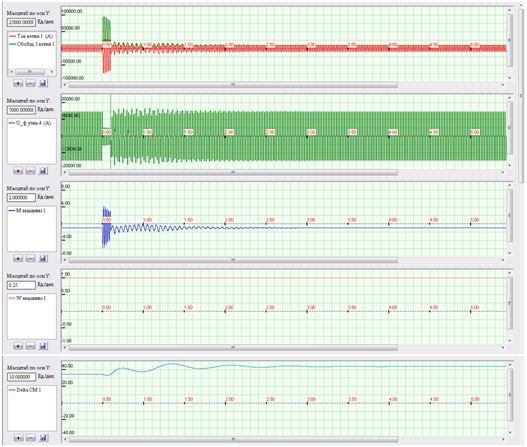
Рисунок 8 – Расчетные осциллограммы восстановления нормального режима генератора при отключении КЗ быстродействующей защитой (масштаб 100 мс / дел)
На рис. 8 (график 1) виден характер изменения тока статора и ОВТ (огибающая линия) в нормальном режиме, при КЗ, и при втягивании генератора в синхронизм. По графику 4 видно, что за время протекания тока КЗ механическое состояние турбоагрегата (скорость вращения) изменилась незначительно. Защита отреагировал на резкое повышение ОВТ.
Далее, после непродолжительных колебаний (угол вылета ротора на графике 5), произошло восстановление синхронного режима с выдачей в сеть номинальной активной мощности (график 3, вращающий момент равен – 1).
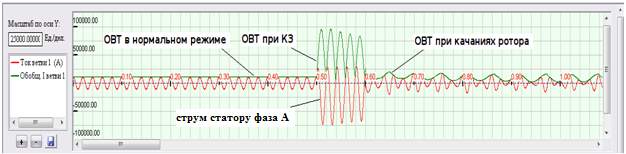
Рисунок 9 – Расчетные осциллограммы восстановления нормального режима генератора при отключении КЗ быстродействующей защитой (масштаб 20 мс / дел)
На рис. 9 представлены осциллограммы тока статора и ОВТ в увеличенном масштабе. На данных кривых видно существенное различие скорости изменения ОВТ в режиме КЗ и при качаниях, в то время как мгновенные и действующие значения токов КЗ могут отличаться от токов синхронизации незначительно. Благодаря этому защита, реагирующая на производную ОВТ по времени, не требует дополнительной отстройки от больших токов при качаниях, что повышает ее чувствительность [10].
Выводы
В работе рассмотрены общие положения вопросов динамической устойчивости электрических систем. Приведенные три способа повышения динамической устойчивости, один из которых рассмотрен досконально.
Был предложен новый принцип действия защит от близких КЗ, основанный на контроле величины скорости изменения (первой производной) обобщенного вектора тока. Так как современные токовые защиты, как правило, реагируют на повышение действующего значения тока короткого замыкания, то для обеспечения селективности их действия возникает необходимость значительного снижения быстродействия защит. Недостаточное быстродействие в некоторых случаях может привести к нарушению динамической устойчивости системы, в частности асинхронном режиме. Поэтому быстродействующая токовая защита, на основе анализа мгновенных значений ОВТ и его первой производной является перспективным сегодня. Для того, чтобы это доказать, было выполнено математическое моделирование близкого к выводам генератора короткого замыкания в программе PowerNet.
Также в данной работе:
- С помощью математического моделирования переходных процессов при близких повреждениях был исследован асинхронный режим генератора, доказана необходимость избегания этого режима.
- Доказано, что в ряде случаев возможно возникновение устойчивого асинхронного хода даже при правильной работе всех систем защиты и автоматики.
- Усовершенствованная дискретная математическая модель для анализа динамических режимов электрической системы, на основе которой создана программа PowerNet.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Андерсон П. Управление энергосистемами и устойчивость / Андерсон П., Фуад А.; пер. с англ. под ред. Я.Н. Лугинского. - М.: Энергия, 1980. - 568 с.
- Устойчивость энергосистемы. Общие сведения. Способы повышения устойчивости [Электронный ресурс]. – Режим доступа: http://electric-zone.ru/ustojchivost-energosistemy....
- Эксплуатация генераторов и синхронных компенсаторов [Электронный ресурс]. – Режим доступа: www.motor-remont.ru/books....
- Гамм Б.З. Исследование переходных процессов в электроэнергетической системе при учете некоторых ее элементов динамическими характеристиками / Б.З. Гамм / / Труды СибНИИЭ. - 1972. - Вып.21. - С.43-48.
- Заболотный И.П. Математическая модель для расчет динамических режимов электрической системы / И.П. Заболотный, С.А. Гришанов / / Вестник Восточноукраинского национального университета. - М.: ВНУ. - 2001. - № 3 (37). - С. 79 - 85.
- Гуревич Ю.Е. Расчеты устойчивости и противоаварийной автоматики в энергосистемам / Гуревич Ю.Е., Либова Л.Е., окинешь А.А. - М.: Энергоатомиздат, 1990. - 390 с.
- Рогозин Г.Г. Программа расчета токов трехфазных короткого замыкания в сложной электрической системе с внедрением принципов функционального моделирования / Г.Г. Рогозин, А.Ю. Коваль / / Моделирование и расчет на ЦВМ режимов энергетических систем. - М.: Наук.думка. - 1977. - С.11-20.
- Сивокобыленко В.Ф. Математическое моделирование электромеханических переходных процессов на электрических станциях / В.Ф. Сивокобыленко, М.А. Меженкова / / журнал «Электричество». - 2001. - № 4. - С.5-9.
- Сивокобыленко В.Ф. Определение параметров эквивалентных схем замещения турбогенераторов для расчетов на математических моделях / В.Ф. Сивокобыленко, М.А. Меженкова / / Сб. наук.працьДонДТУ.Серия «Электротехника и энергетика». -Донецк: ДонГТУ. - 2000. - Вып. 17. - С. 38- 41.
- Авраменко В.Н. Моделирование электроэнергетических систем - достижения и перспективы научных исследований / В.Н. Авраменко / / Техническая электродинамика. - 1997. - № 1. - С.73-80.
