Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования и предполагаемые результаты
- 3. Аналитический обзор
- 4. Исследовательская часть
- 4.1 Моделирование конструкции мостового крана
- 4.2 Определение частот собственных колебаний
- 4.3 Получение графиков переходных процессов
- 4.4 Математическое описание линейной двухмассовой системы мостового крана
- 4.5 Синтез регулятора для гашения колебаний
- 4.6 Проверка результатов на модели с распределенными параметрами
- Выводы
- Список источников
Введение
В современном производственном процессе транспортировка является неотъемлемым этапом, поскольку невозможно реализовать все этапы производства на одной линии. При этом для перемещения больших грузов используются крановые установки. В зависимости от конструкции и назначения они могут иметь механизмы горизонтального перемещения, подъема и опускания груза и поворота.
Один из типов таких установок - мостовой кран. Эта установка достаточно широко используется в различных отраслях промышленности, например, в металлургии.
1. Актуальность темы
Мостовой кран осуществляет горизонтальные перемещения грузов, используя механизмы поступательного движения. В зависимости от условий эксплуатации они могут иметь только один такой механизм (для использования в закрытых помещениях) или два, которые осуществляют движение в перпендикулярных направлениях (универсальные). При этом длина конструкции достигает нескольких десятков метров, что обуславливает распределение жесткости вдоль ее длины. При таких обстоятельствах собственные упругие колебания конструкции достигают достаточно существенных значений, что приводит к значительному росту механических напряжений в ее элементах [1, 2, 3]. Учитывая гармонический характер переходных процессов упругих колебаний, срок эксплуатации всей крановой установки уменьшается из-за явления усталости металла. Это обусловливает необходимость создания средств для гашения таких колебаний.
2. Цель и задачи исследования и предполагаемые результаты
На основе имеющихся данных о параметрах конструкции мостового крана создать ее компьютерные модели, которые достаточно точно отражают ее динамические свойства, и разработать методику гашения упругих колебаний. Проверить влияние полученного закона управления на гашение колебаний груза. Подтвердить адекватность полученных результатов на экспериментальной установке.
Для достижения обозначенной цели в работе необходимо решить следующие задачи:
- создать компьютерную модель конструкции мостового крана, которая учитывает распределение массы и упругости по ее длине;
- на основе анализа полученных графиков переходных процессов создать упрощенную линеаризованную модель моста;
- синтезировать регулятор для гашения упругих колебаний конструкции и проверить его эффективность на обеих моделях;
- дополнить модель учётом колебаний груза и проверить качество работы системы;
- синтезировать наблюдатель для восстановления полного вектора состояний системы;
- реализовать указанные алгоритмы на микроконтроллере семейства Arduino и экспериментально подтвердить полученные ранее результаты.
Объект исследования: компьютерная модель мостового крана с учетом распределения массы и упругости.
Предмет исследования: гашение упругих колебаний конструкции моста.
Основные научные и практические результаты, их значение:
- Использование специализированного программного обеспечения позволяет проводить исследования упругих свойств механических конструкций, как в переходных режимах, так и с точки зрения гармонического спектра колебаний.
- При расположении тележки в средней точке моста и её неподвижном закреплении динамику перемещения моста можно с достаточной точностью описать уравнениями движения двухмассовой электромеханической системы, предварительно заменив распределенные параметры сосредоточенными.
- Если есть возможность измерения или идентификации физических величин, соответствующих переменным состояния двухмассовой электромеханической системы, упругие колебания конструкции моста можно эффективно гасить, синтезировав модальный регулятор.
3. Аналитический обзор
Упругость конструкции как и её масса являются распределенными, причем характер такого распределения зависит от построения крановой установки, положения тележки с грузом, массы груза и т.п. Итак, анализ упругих свойств механической конструкции традиционными методами неэффективен, поскольку замена распределенных параметров сосредоточенными требует точного расчета собственных частот колебаний.
Для удобства проведения таких исследований создано много программных пакетов, которые описывают переходные процессы в системах с распределенными параметрами с помощью дифференциальных уравнений в частных производных (ДУЧП). В основу функционирования таких пакетов положен метод конечных элементов [8], который предполагает разбиение всей системы на конечные элементы определенной формы и решения ДУЧП в узловых точках. С помощью таких пакетов удобно проводить анализ адекватности принятых методов замены распределенных параметров сосредоточенными и свойств систем, которые составят основу для синтеза системы регулирования.
Традиционно анализ упругих колебаний в механических системах проводят путем представления всей конструкции совокупностью масс с упругими связями между ними, т.е. представлением всей конструкции в виде многомассовой системы [3]. При этом выделяют наиболее существенные частоты колебаний и, в зависимости от их количества, выбирают порядок системы. Если в системе присутствует только одна существенная частота собственных колебаний, то её динамические свойства с достаточной степенью точности будет передавать двухмассовая система. Для неё существует много методов гашения упругих колебаний, однако наибольший интерес вызывает применение модального управления. При этом динамические свойства замкнутой системы определяться расположением ее полюсов, которое зависит от коэффициентов обратных связей по переменным состояния системы. Если же есть возможность измерения или идентификации этих переменных, то путем подбора расположения полюсов можно получить желаемый характер переходных процессов, который в данном случае предусматривает гашение упругих колебаний конструкции.
4. Исследовательская часть
Посвящена созданию компьютерной модели упругой конструкции мостового крана, упрощению её математического описания, синтезу системы модального регулирования и анализу эффективности гашения упругих колебаний.
4.1 Моделирование конструкции мостового крана
Анализ упругих колебаний систем с распределенными параметрами, к которым относится и конструкция мостового крана, удобно проводить в специализированных программных пакетах, которые моделируют поведение таких систем путем решения ДУЧП. Пакет Comsol Multiphysics позволяет проводить анализ установившихся режимов и переходных процессов, расчет частот собственных колебаний и логарифмических амплитудно-частотных характеристик.
Упрощенная модель конструкции моста в этом пакете приведена на рис. 1. Входными параметрами для нее являются геометрическая конфигурация конструкции моста и тележки, а также механические свойства материала, из которого они изготовлены: плотность, модуль упругости и коэффициент Пуассона.
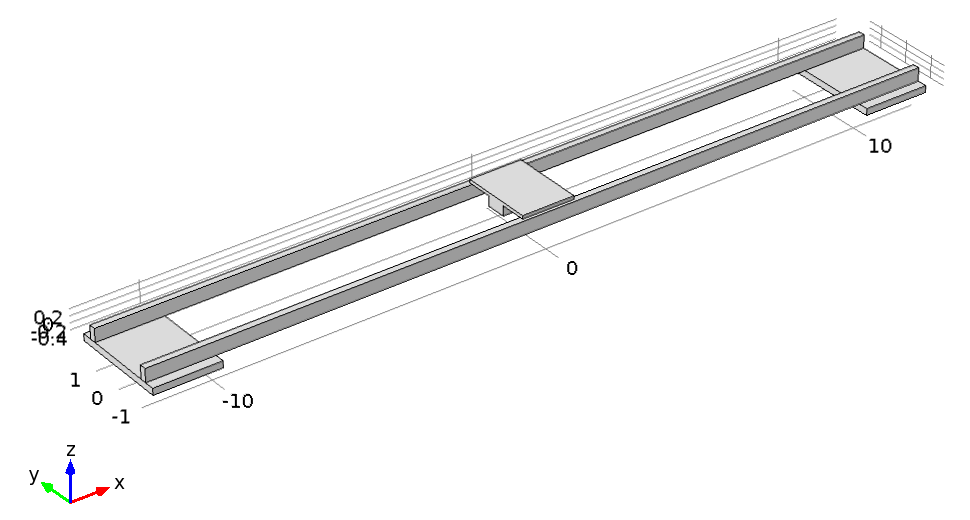
Рисунок 1 – Модель конструкции мостового крана
Итак, мост состоит из двух сплошных металлических балок прямоугольного сечения со сниженными значениями плотности и модуля упругости. За основу взяты стандартные данные для строительной стали, но плотность была снижена так, чтобы масса конструкции совпадала с данными реальной установки. Модуль упругости был снижен пропорционально массе, чтобы частоты собственных колебаний оставались без изменения.
Зададимся фиксированным положением тележки в центральной точке моста. Такое упрощение позволяет проводить все необходимые исследования с достаточной степенью точности без дополнительных затрат вычислительного времени.
4.2 Определение частот собственных колебаний
Для определения частот собственных колебаний конструкции мостового крана накладываются необходимые ограничения на движение, которые будут присутствовать при моделировании динамики системы. В данном случае мы запрещаем движение конструкции вдоль осей Х и Z (см. рис. 1).
На рис. 2-5 приведены первые четыре режима собственных колебаний конструкции. Из литературы [1, 2, 3] известно, что эти частоты обычно составляют несколько Герц, что и получено в результате моделирования.
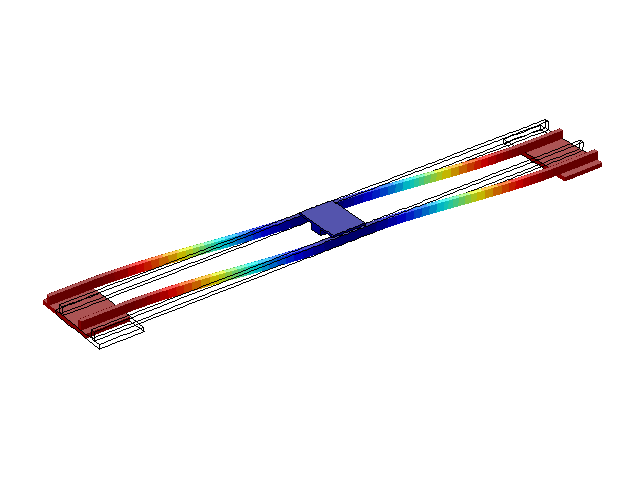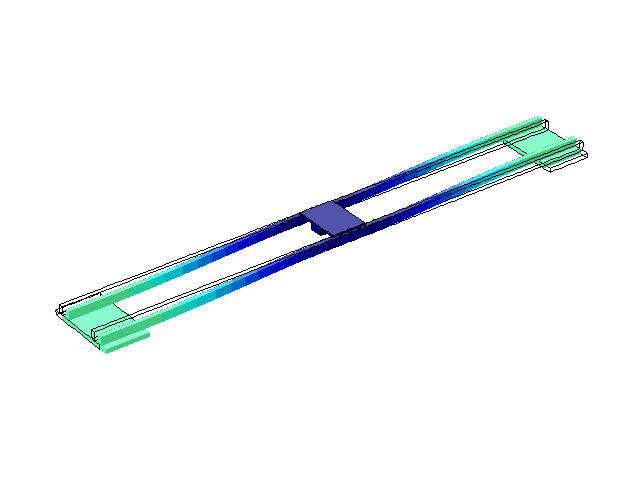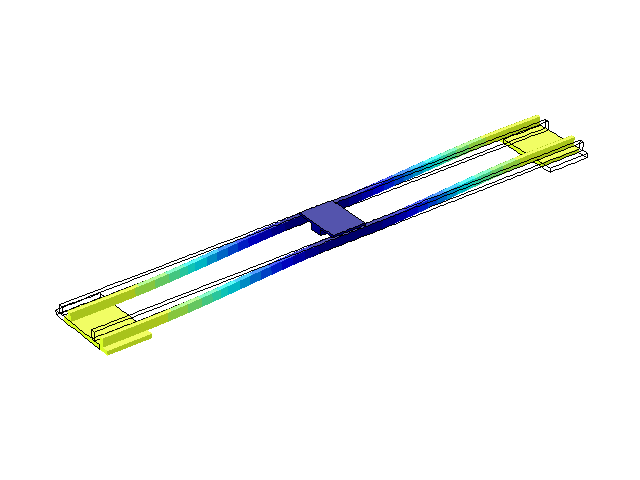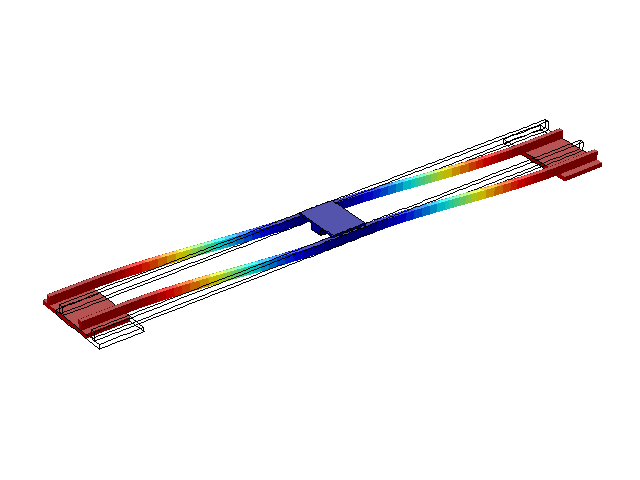
Рисунок 2 – Режим собственных колебаний моста при частоте f=0,61 Гц
(анимация: 24 кадра, бесконечное повторение, 273 килобайта)
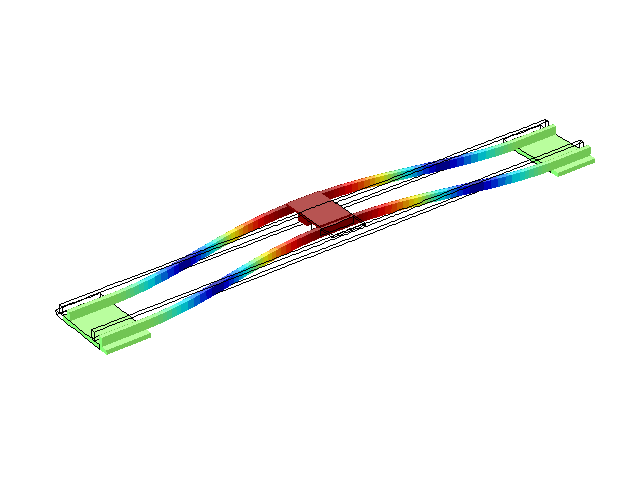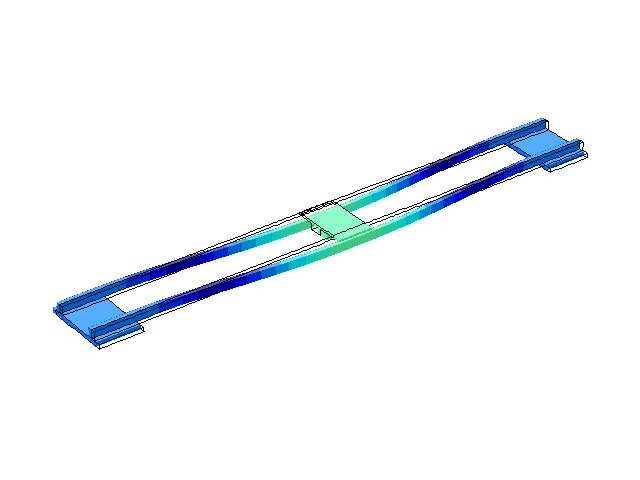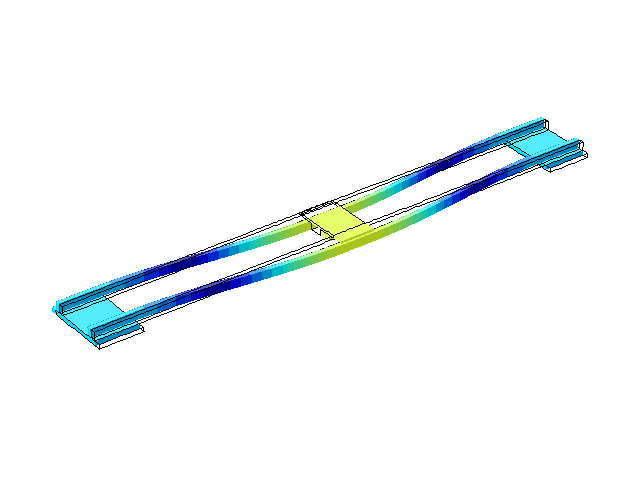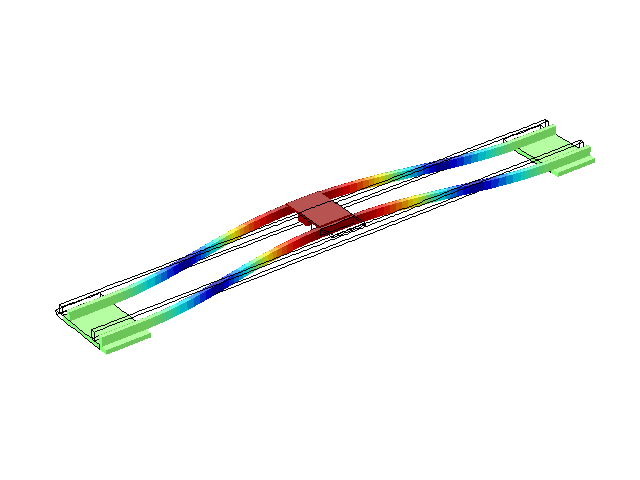
Рисунок 3 – Режим собственных колебаний моста при частоте f=1,18 Гц
(анимация: 24 кадра, бесконечное повторение, 279 килобайта)
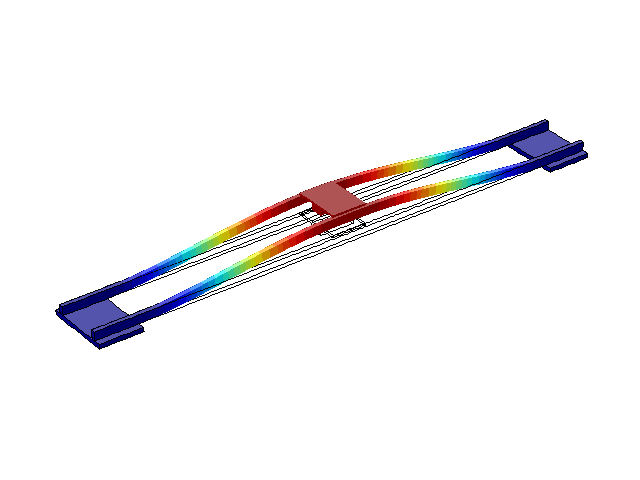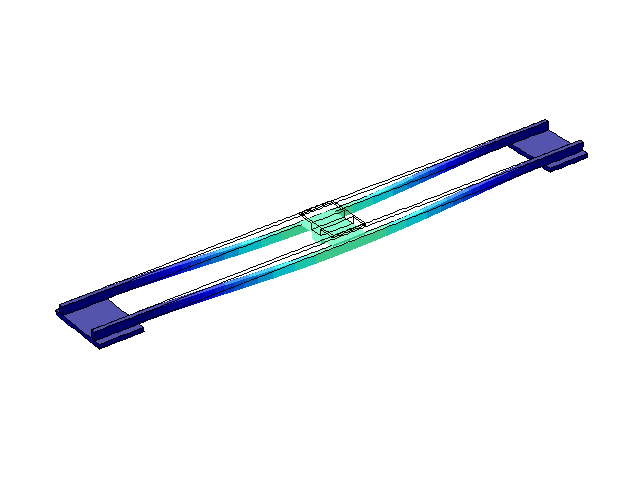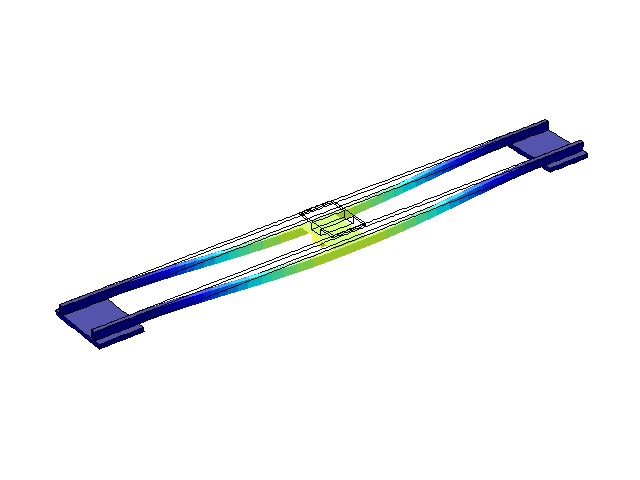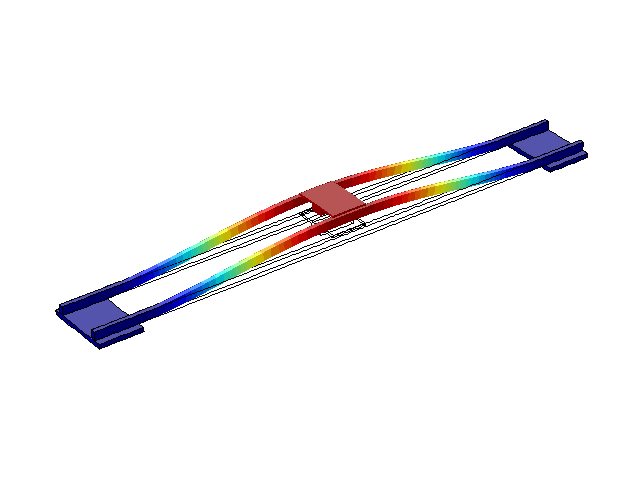
Рисунок 4 – Режим собственных колебаний моста при частоте f=1,76 Гц
(анимация: 24 кадра, бесконечное повторение, 275 килобайта)
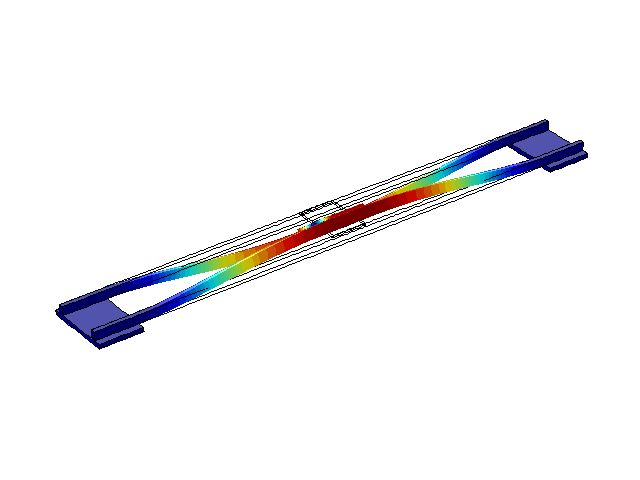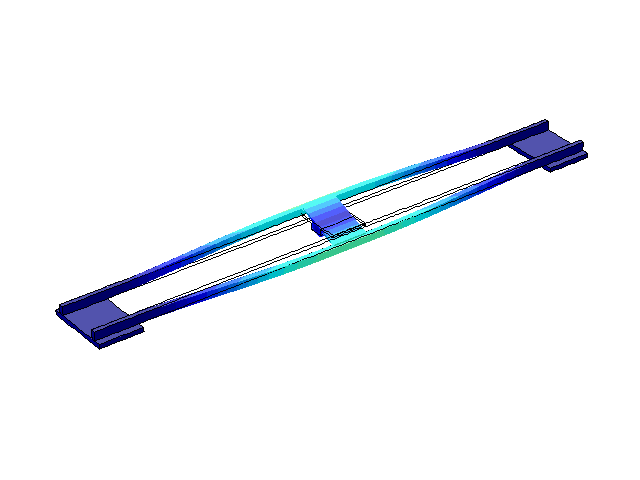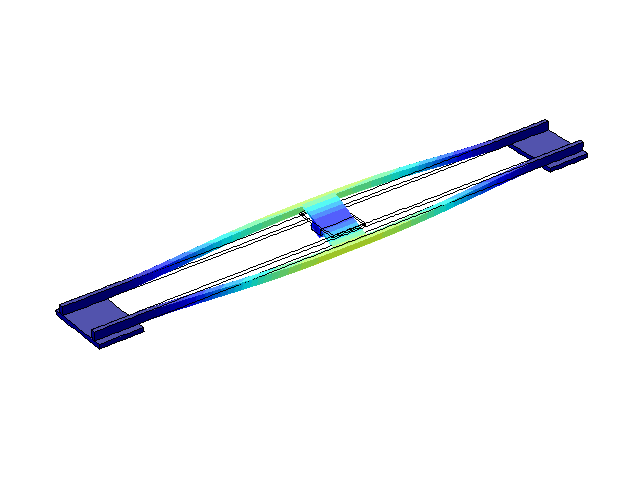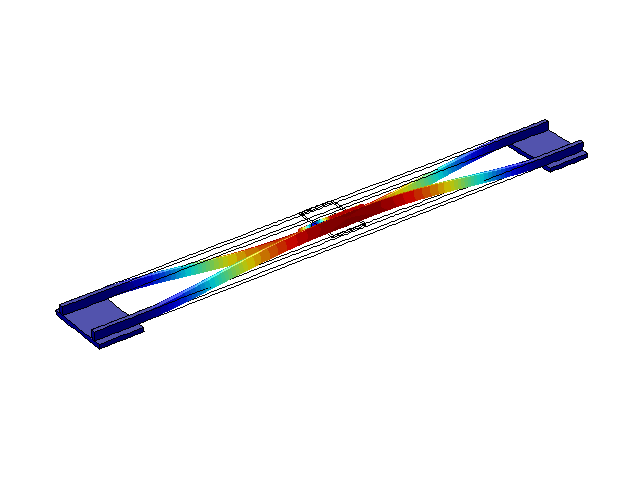
Рисунок 5 – Режим собственных колебаний моста при частоте f=3,31 Гц
(анимация: 24 кадра, бесконечное повторение, 289 килобайта)
4.3 Получение графиков переходных процессов
Графики переходных процессов при перемещении моста получены с упрощением, что приводные моменты двигателей создают усилие, которое равномерно распределяется по плоскости конечных граней модели [7].
Усилие, приложенное к мосту, соответствует разгону до скорости 0.5 м/с за 1 с и аналогичному торможению через 7 с движения на установившейся скорости. Результаты моделирования показали, что при условии расположения тележки в центральной точке моста, скорости и перемещения его крайних точек абсолютно равны.
Графики изменения скорости крайних точек моста v1 и тележки v2, а также максимальной деформации моста в направлении его движения Δs2, которая измеряется в его центральной точке, приведены на рис. 6. Из графиков видно, что в обоих крайних точках имеют место недемпфированные колебания, причем амплитуда колебаний скорости достигает значения 0.1 м/с.
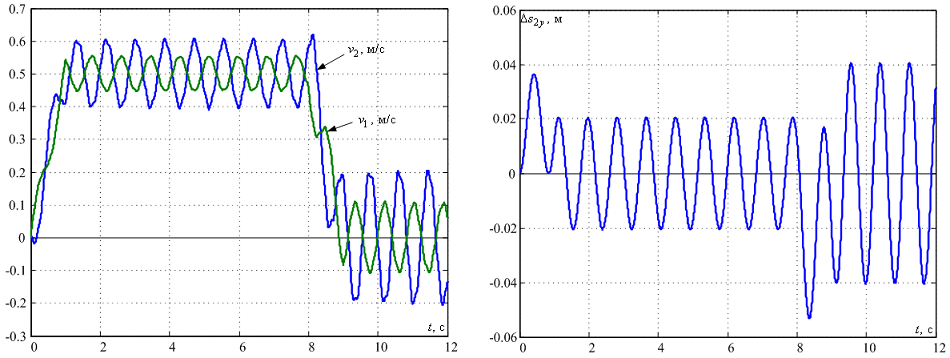
Рисунок 6 – Переходные процессы движения упругой конструкции мостового крана
Очевидно, что существенное влияние на переходные процессы имеет лишь одна гармоничное составляющая, которая соответствует режиму собственных колебаний с частотой f=1.18 Гц, как показано на рис. 3. График переходных процессов по скорости показывает, что в спектре колебаний присутствует как минимум еще одна гармоническая составляющая, однако ее амплитуда значительно меньше основной, а потому её влиянием можно пренебречь. Поэтому считаем, что процесс упругих колебаний с достаточной степенью точности описывается с помощью консервативного звена, передаточная функция которого имеет вид:
Такое описание соответствует поведению многомассовой электромеханической системы, которую примем за основу при создании упрощенной математической модели.
4.4 Математическое описание линейной двухмассовой системы мостового крана
В наиболее общем случае мост необходимо рассматривать как трёхмассовую электромеханическую систему [4], кинематическая схема которой представлена на рис. 7а.
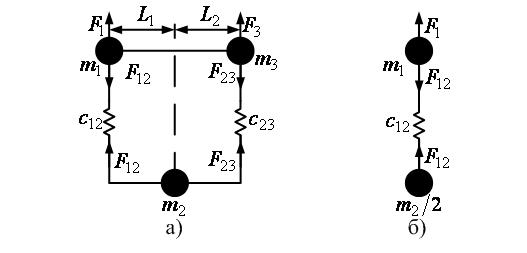
Рисунок 7 – Кинематические модели моста
В таком случае мост условно представлен в виде трех сосредоточенных масс – крайних точек m1 и m3, связанными упругими связями с коэффициентами жесткости c12 и c23 с точкой m2, в которой находится тележка.
Если тележка расположена в средней точке моста (L1=L2), то и коэффициенты жесткости должны быть одинаковыми. Если при этом равны друг другу массы, сосредоточенные на концах моста, а также приложенные к ним силы, кинематическую схему моста можно упростить до двухмассовой, оставив только одну из опор (крайних точек) и центральную точку, уменьшив её массу вдвое, как это показано на рис. 7б. Математическое описание такой системы будет выглядеть:
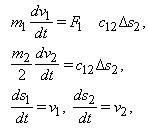
где F1 – сила, приложенная к первой массе, F12 – упругая сила, Δs2=s1-s2 – величина упругой деформации.
При известных значениях сосредоточенных масс и постоянной времени упругих колебаний двухмассовой системы T12=1/2πf коэффициент жёсткости можно рассчитать по формуле:
Итак одним из главных вопросов при моделировании в данном случае является выбор величин сосредоточенных масс.
В результате исследований линейной модели установлено, что при изменении распределения массы моста между опорами и местом нахождения тележки желаемая частота упругих колебаний достигается при различных амплитудах сигналов v1 и v2. Лучшее совпадение этих амплитуд с результатами, полученными в пакете Comsol, обеспечивается при расчете сосредоточенных масс по формулам:
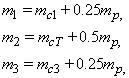
где mc1,3 – сосредоточенные массы первой и второй опор соответственно, включающие массу колес, электроприводов и концевых балок, mh – распределенная масса главных балок моста, mcT – сосредоточенная масса тележки. Такое распределение масс совпадает с рекомендациями, приведенными в [1], хотя в некоторых источниках предлагается массу моста распределять равномерно между опорами, без средней точки [2].
Результаты моделирования линейной двухмассовой системы с рекомендуемыми параметрами приведены на рис. 8, из которого видно, что полученная модель достаточно точно отражает процесс перемещения конструкции, полученный в пакете Comsol Mutiphysics [10]. При этом амплитуда колебаний скорости второй массы несколько меньше по сравнению с графиками рис. 6. Однако эти различия несущественны, а потому для этой модели проведем синтез регулятора для гашения колебаний.
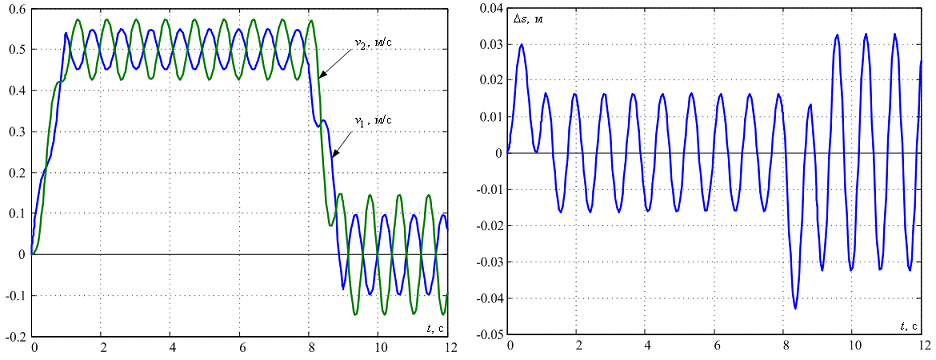
Рисунок 8 – Переходные процессы в линеаризованной системе
4.5 Синтез регулятора для гашения колебаний
Одним из возможных вариантов является применение регулятора с линейной обратной связью по полному вектору состояния системы, структурная схема которой приведена на рис. 9 [9].
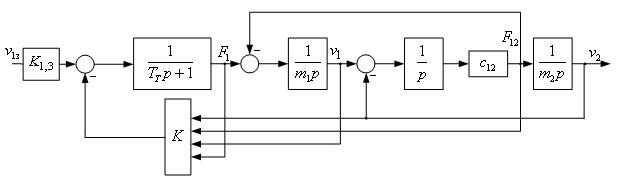
Рисунок 9 – Структурная схема двухмассовой системы с регулятором
Контур регулирования тока представляем в виде апериодического звена с постоянной времени TT=0.001 с. Влиянием перекрестных связей для электроприводов переменного тока и внутренней обратной связи по ЭДС вращения двигателя пренебрегаем. Тогда получим такой вектор состояния системы:
Коэффициенты модального регулятора рассчитываем по коэффициентам αi желаемого характеристического полинома, которые определяют динамику системы. В результате синтеза получены следующие выражения для коэффициентов регулятора состояния:
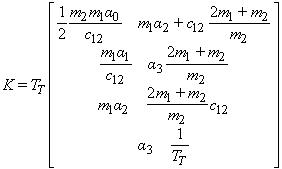
Результаты моделирования системы с таким регулятором при использовании распределения Бесселя со среднегеометрическим корнем Ω0=1/(8TT), приведены на рис. 10. Видим, что колебания в системе отсутствуют, а максимальное значение отклонения средней точки моста уменьшилось по сравнению с результатами, приведенными на рис. 8 почти вдвое.
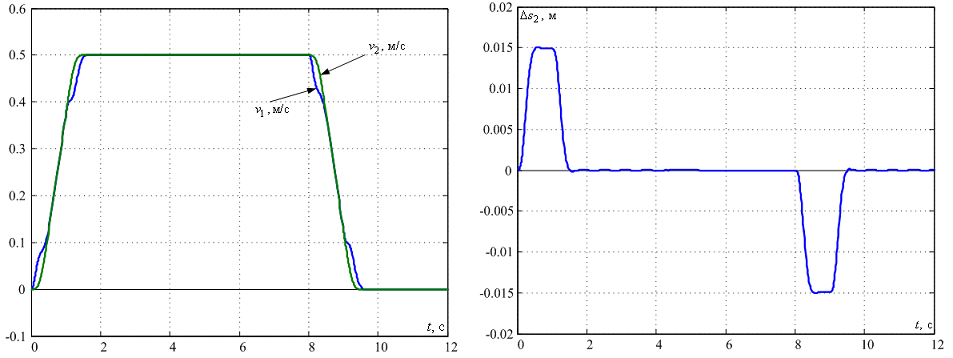
Рисунок 10 – Переходные процессы в линейной модели с регулятором состояния
Следует учитывать, что линейная модель является приближенной, поэтому необходимо проверять адекватность полученных результатов на модели с распределенными параметрами [6].
4.6 Проверка результатов на модели с распределенными параметрами
Для этого приложим к модели моста в программном пакете Comsol линейную силу, полученную в системе с модальным регулятором на выходе контура тока. Результаты моделирования приведены на рис. 11.
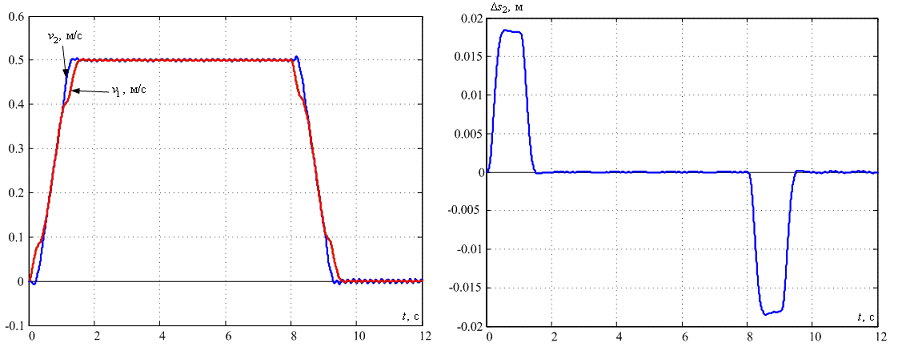
Рисунок 11 – Переходные процессы в модели с распределенными параметрами при подаче на неё выходного сигнала контура тока в системе с регулятором состояния
Видим, что низкочастотные упругие колебания полностью гасятся. При этом остаются незначительные колебания более высокой частоты, не учтенные в линейной модели. Тем не менее, результаты моделирования совпадают с полученными на линейной модели, что подтверждает ее адекватность.
Дальнейшие исследования, выполненные в Comsol, показали, что при фиксации тележки в других точках моста характер упругих колебаний моста существенно изменяется: появляются дополнительные частоты, изменяющиеся в широком диапазоне. Это делает невозможным применение синтезированного модального регулятора при большом диапазоне перемещений тележки. Для синтеза адаптивной системы управления можно использовать линейную модель моста на основании трехмассовой кинематической схемы рис. 7а, в которой изменение положения тележки учитывается изменением коэффициентов упругости и распределения масс.
В этом случае перспективным представляется расчет нескольких модальных регуляторов, соответствующих различным положениям тележки, и плавный переход от одной настройки к другой при помощи нечеткого регулятора типа Сугено [5].
Выводы
Получена компьютерная модель конструкции мостового крана в программном пакете Comsol Multiphysics, которая учитывает распределение массы и упругости по ее длине и позволяет исследовать ее упругие колебания. На основе полученных графиков переходных процессов была создана упрощенная линеаризованная модель, позволяющая проводить синтез регуляторов для гашения упругих колебаний конструкции.
Наиболее существенные выводы и рекомендации заключаются в следующем:
- Анализ упругих свойств механических конструкций удобно проводить с помощью специализированного программного обеспечения, которое использует метод конечных элементов.
- При перемещении моста существенное влияние на его движение оказывает только одна гармоническая составляющая упругих колебаний.
- При условии, когда неподвижная тележка находится в центральной точке моста, динамические свойства конструкции моста можно представить в виде двомасовой электромеханической системы.
- Использование модального регулятора позволяет эффективно гасить упругие колебания конструкции моста, если есть возможность получить информацию о всех имеющихся переменных состояния в любой момент времени.
Примечание. При написании данного реферата дипломная работа находится на стадии выполнения, поэтому приведенный реферат содержит имеющиеся на момент сдачи экзамена по дисциплине «Интернет-технологии» информацию. Конечный срок выполнения магистерской работы и дата защиты диплома – январь 2014 года.
Список источников
- Будіков Л.Я. Багатопараметричний аналіз динаміки вантажопідйомних кранів мостового типу: Монографія. – Луганськ, вид-во СНУ ім. В.Даля, вид. 2-е, 2003. – 210 с.
- Макурин А.В., Морозов Д.И. Динамика продольного перемещения мостового крана с учетом упругости элементов конструкции // Електротехнічні та комп’ютерні системи. – 2011. – №3(79). – С. 167-169.
- A. Buch. Optimale Bewegungssteuerung von schwingungsfahigen mechatronischen Systemen mit zwei Freiheitsgraden am Beispiel eines Krans mit Pendelnder Last und elastischer Mechanik – Magdeburg, 1999. – 250 S.
- B. Jerman. An enhanced mathematical model for investigating the dynamic loading of a slewing crane [Электронный ресурс]: / B. Jerman. – Электрон. текст. дан. – Slovenia: 2006. – Режим доступа: http://pic.sagepub.com/content/220/4/421
- C.Y. Chang. The switching algorithm for the control of overhead crane [Электронный ресурс]: / C.Y. Chang. – Электрон. текст. дан. – China: 2006. – Режим доступа: http://link.springer.com/article/10.1007%2Fs00521-006-0036-z
- E. Reynders. Reference-based combined deterministic-stochastic subspace identification for experimental and operational modal analysis [Электронный ресурс]: / E. Reynders, G. De Roeck. – Электрон. текст. дан. – Belgium: 2008. – Режим доступа: http://www.sciencedirect.com/science/article/pii/S0888327007001823
- F.L. Chernousko. Control of elastic systems by bounded distributed forces [Электронный ресурс]: / F.L. Chernousko. – Электрон. текст. дан. – Russia: 1996. – Режим доступа: http://www.sciencedirect.com/science/article/pii/009630039600001X
- K.A.F. Moustafa. Modelling and control of overhead cranes with flexible variable-length cable by finite element method [Электронный ресурс]: / K.A.F. Moustafa, E.H. Gad, A.M.A. El-Moneer, M.I.S. Ismail. – Электрон. текст. дан. – Egypt: 2005. – Режим доступа: http://tim.sagepub.com/content/27/1/1.abstract
- N. Uchiyama. Robust control of rotary crane by partial-state feedback with integrator [Электронный ресурс]: / N. Uchiyama. – Электрон. текст. дан. – Japan: 2009. – Режим доступа: http://www.sciencedirect.com/science/article/pii/S0957415809001500
- 10. Y. Sakawa. Nonlinear model and linear robust control of overhead traveling cranes [Электронный ресурс]: / Y. Sakawa, H. Sano. – Электрон. текст. дан. – Japan: 1997. – Режим доступа: http://www.sciencedirect.com/science/article/pii/S0362546X97860415
