Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження та передбачувані результати
- 3. Аналітичний огляд
- 4. Дослідницька частина
- 4.1 Моделювання конструкції мостового крану
- 4.2 Визначення частот власних коливань
- 4.3 Отримання графіків перехідних процесів
- 4.4 Математичний опис лінійної двомасової системи мостового крану
- 4.5 Синтез регулятора для гасіння коливань
- 4.6 Перевірка результатів на моделі з розподіленими параметрами
- Висновки
- Перелік посилань
Вступ
У сучасному виробничому процесі транспортування є невід’ємним етапом, оскільки неможливо реалізувати всі етапи виробництва на одній лінії. При цьому для переміщення великих вантажів використовуються кранові установки. В залежності від конструкції та призначення вони можуть мати механізми горизонтального переміщення, підйому та опускання вантажу, та повороту.
Один із типів таких установок – мостовий кран. Ця установка достатньо широко використовується у різних галузях промисловості, наприклад, у металургії.
1. Актуальність теми
Мостовий кран здійснює горизонтальні переміщення вантажів, використовуючи механізми поступального руху. В залежності від умов експлуатації вони можуть мати лише один такий механізм (для використання у закритих приміщеннях) чи два, які здійснюють рух у перпендикулярних напрямках (універсальні). При цьому довжина конструкції досягає кількох десятків метрів, що зумовлює розподіл жорсткості уздовж її довжини. За таких обставин власні пружні коливання конструкції досягають достатньо суттєвих значень, що призводить до значного зростання механічних напружень в її елементах [1, 2, 3]. Враховуючи гармонічний характер перехідних процесів пружних коливань, термін експлуатації всієї кранової установки зменшується через явище утоми металу. Це обумовлює необхідність створення засобів для гасіння таких коливань.
2. Мета і задачі дослідження та передбачувані результати
На основі наявних даних про параметри конструкції мостового крану створити її комп’ютерні моделі, які достатньо точно відображають її динамічні властивості і розробити методику гасіння пружних коливань. Перевірити вплив отриманого закону керування на гасіння коливань вантажу. Підтвердити адекватність отриманих результатів на експериментальному встаткуванні.
Для досягнення позначеної мети в роботі необхідно розв’язати такі задачі:
- створити комп’ютерну модель конструкції мостового крану, яка враховує розподіл маси і пружності по її довжині;
- на основі аналізу отриманих графіків перехідних процесів створити спрощену лінеаризовану модель моста;
- синтезувати регулятор для гасіння пружних коливань конструкції і перевірити його ефективність на обох моделях;
- доповнити модель урахуванням коливань вантажу й перевірити якість роботи системи;
- синтезувати спостерігач для відновлення повного вектора станів системи;
- реалізувати зазначені алгоритми на мікроконтролері сімейства Arduino та експериментально підтвердити отримані раніше результати.
Об’єкт дослідження: комп’ютерна модель мостового крану із урахуванням розподілу маси і пружності.
Предмет дослідження: гасіння пружних коливань конструкції моста.
Основні наукові та практичні результати, їх значення:
- Використання спеціалізованого програмного забезпечення дозволяє проводити дослідження пружних властивостей механічних конструкцій, як в перехідних режимах, так і з точки зору гармонічного спектру коливань.
- При розташуванні візка у середній точці моста і його нерухомому закріпленні динаміку переміщення моста можна із достатньою точністю описати рівняннями руху двомасової електромеханічної системи, попередньо замінивши розподілені параметри зосередженими.
- Якщо є можливість вимірювання або ідентифікації фізичних величин, які відповідають змінним стану двомасової електромеханічної системи, пружні коливання конструкції моста можна ефективно гасити, синтезувавши модальний регулятор.
3. Аналітичний огляд
Пружність конструкції як і її маса є розподіленими, при чому характер такого розподілу залежить від побудови кранової установки, положення візка із вантажем, маси вантажу тощо. Отже аналіз пружних властивостей механічної конструкції традиційними методами є неефективним, оскільки заміна розподілених параметрів зосередженими вимагає точного розрахунку власних частот коливань.
Для удобства проведения таких исследований создано много программных пакетов, которые описывают переходные процессы в системах с распределенными параметрами с помощью дифференциальных уравнений в частных производных (ДУЧП). Для зручності проведення таких досліджень створено багато програмних пакетів, які описують перехідні процеси в системах з розподіленими параметрами за допомогою диференційних рівнянь у часткових похідних (ДРЧП). В основу функціонування таких пакетів покладено метод кінцевих елементів [8], який передбачає розбиття всієї системи на кінцеві елементи визначеної форми і розв’язання ДРЧП у вузлових точках. За допомогою таких пакетів зручно проводити аналіз адекватності прийнятих методів заміни розподілених параметрів зосередженими і властивостей систем, що становитимуть основу для синтезу системи регулювання.
Традиційно аналіз пружних коливань у механічних системах проводять шляхом представлення всієї конструкції сукупністю мас із пружними зв’язками між ними, тобто представленням всієї конструкції у вигляді багатомасової системи [3]. При цьому виділяють найбільш суттєві частоти коливань і, в залежності від їх кількості, обирають порядок системи. Якщо у системі присутня лише одна суттєва частота власних коливань, то її динамічні властивості із достатнім ступенем точності передаватиме двомасова система. Для неї існує багато методів гасіння пружних коливань, проте найбільший інтерес викликає застосування модального керування. При цьому динамічні властивості замкненої системи визначатимуться розташуванням її полюсів, яке залежить від коефіцієнтів зворотних зв’язків за змінними стану системи. Якщо є можливість вимірювання або ідентифікації цих змінних, то шляхом підбору розташування полюсів можна отримати бажаний характер перехідних процесів, що у даному випадку передбачає гасіння пружних коливань конструкції.
4. Дослідницька частина
Присвячена створенню комп’ютерної моделі пружної конструкції мостового крану, спрощенню її математичного опису, синтезу системи модального регулювання і аналізу ефективності гасіння пружних коливань.
4.1 Моделювання конструкції мостового крану
Аналіз пружних коливань систем із розподіленими параметрами, до яких відноситься і конструкція мостового крану, зручно проводити у спеціалізованих програмних пакетах, які моделюють поведінку таких систем шляхом розв’язання ДРЧП. Пакет Comsol Multiphysics дозволяє проводити аналіз усталених режимів і перехідних процесів, розрахунок частот власних коливань і логарифмічних амплітудно-частотних характеристик.
Спрощена модель конструкції моста у цьому пакеті наведено на рис. 1. Вхідними параметрами для неї є геометрична конфігурація конструкції моста і візка, а також механічні властивості матеріалу, з якого вони виготовлені: щільність, модуль пружності та коефіцієнт Пуасона.
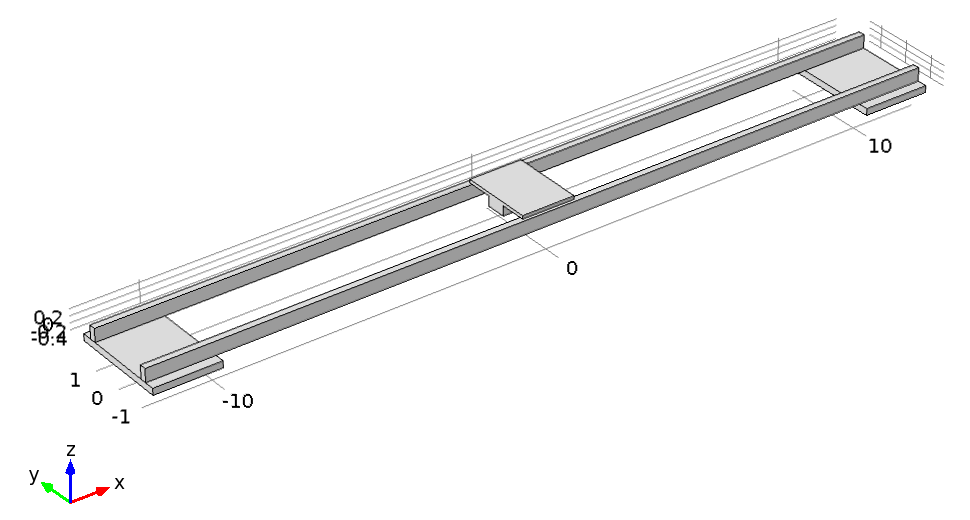
Рисунок 1 – Модель конструкцїї мостового крану
Отже, міст складається з двох суцільних металевих балок прямокутного перерізу із заниженими значеннями щільності і модулю пружності. За основу взято стандартні дані для будівельної сталі, але щільність було занижено так, щоб маса конструкції співпадала з даними реальної установки. Модуль пружності було знижено пропорційно масі, щоб частоти власних коливань залишалися без зміни.
Задамося фіксованим положенням візка у центральній точці моста. Таке спрощення дозволяє проводити всі необхідні дослідження із достатнім ступенем точності без додаткових витрат обчислювального часу.
4.2 Визначення частот власних коливань
Для визначення частот власних коливань конструкції мостового крану накладаються необхідні обмеження на рух, які будуть присутні при моделюванні динаміки системи. В даному випадку ми забороняємо рух конструкції вздовж осей Х і Z (див. рис. 1).
На рис. 2-5 наведені перші чотири режими власних коливань конструкції. З літератури [1, 2, 3] відомо, що ці частоти зазвичай складають декілька Герц, що й отримано в результаті моделювання.
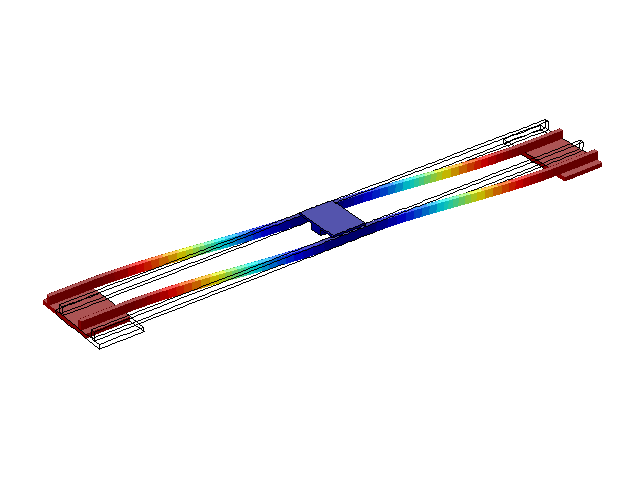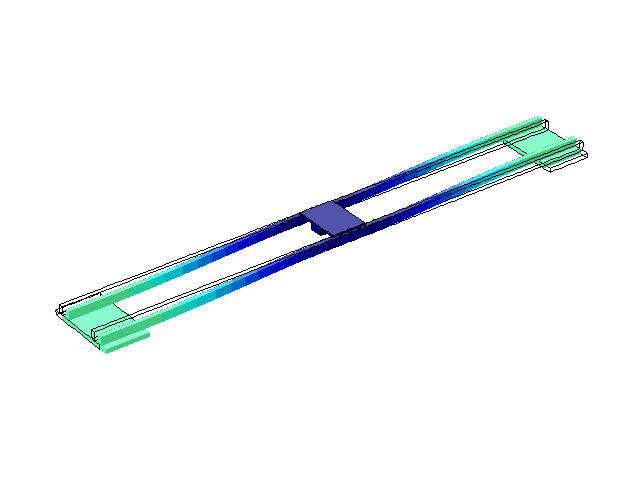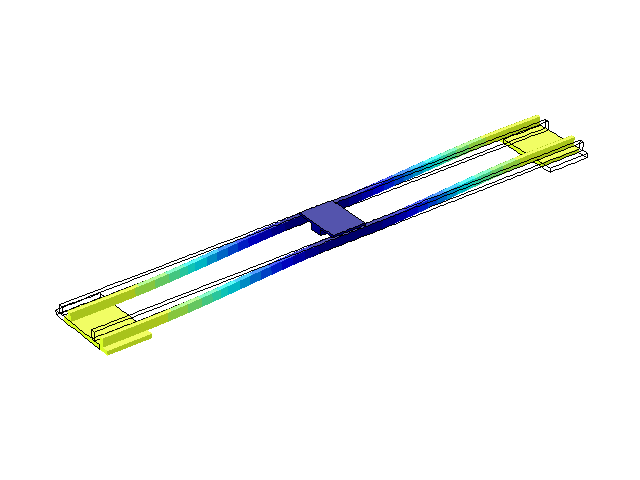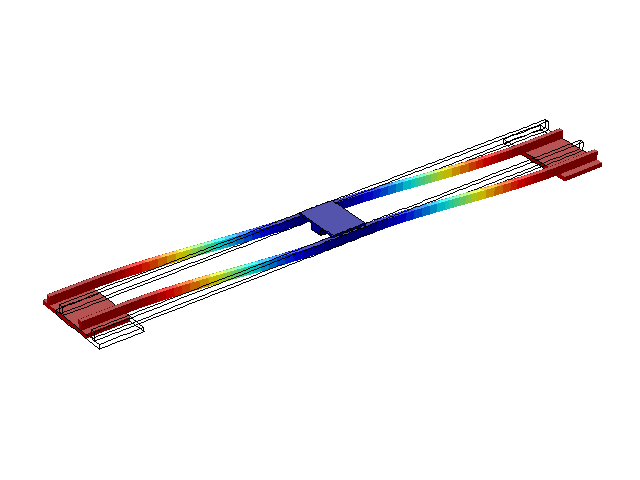
Рисунок 2 – Режим власних коливань моста при частоті f=0,61 Гц
(анімація: 24 кадри, нескінченне повторення, 273 килобайти)
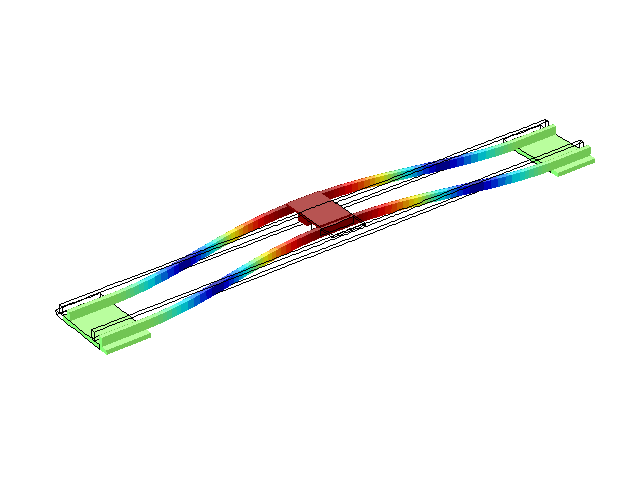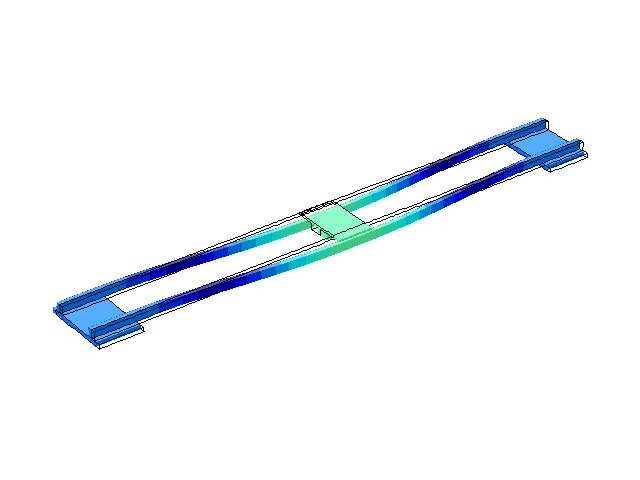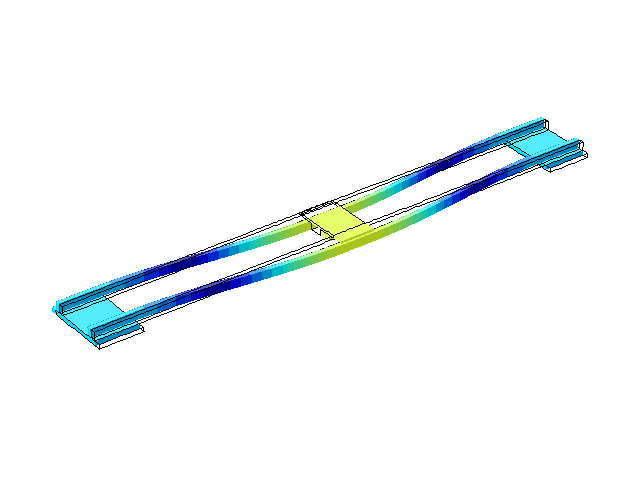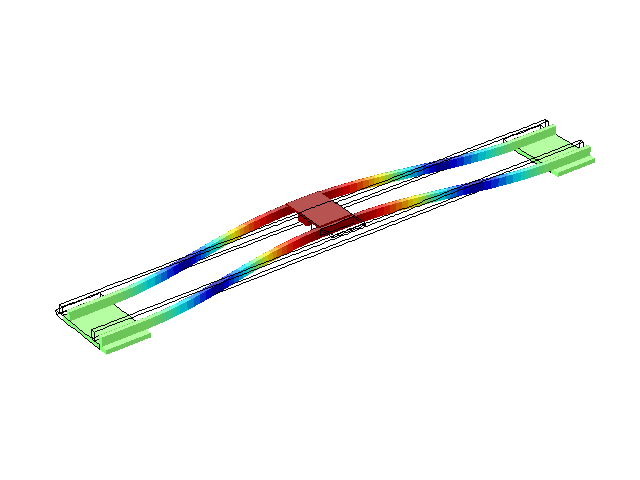
Рисунок 3 – Режим власних коливань моста при частоті f=1,18 Гц
(анімація: 24 кадри, нескінченне повторення, 279 килобайти)
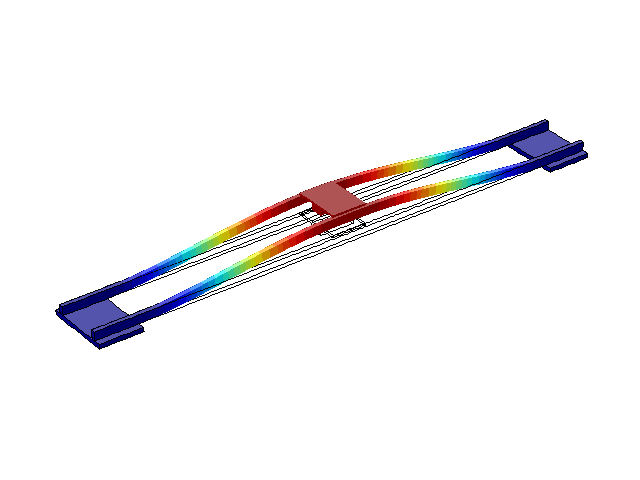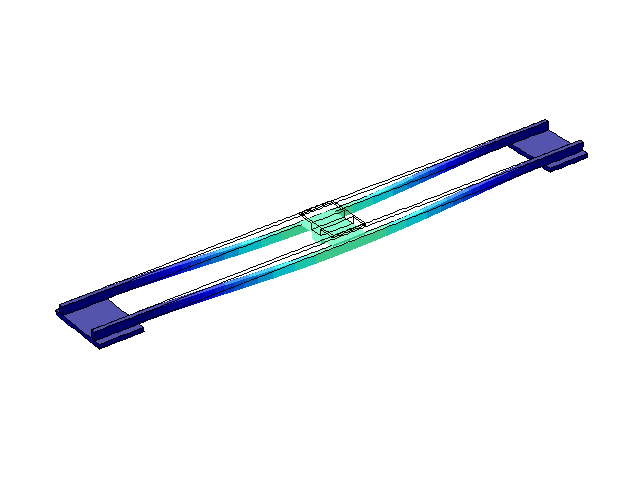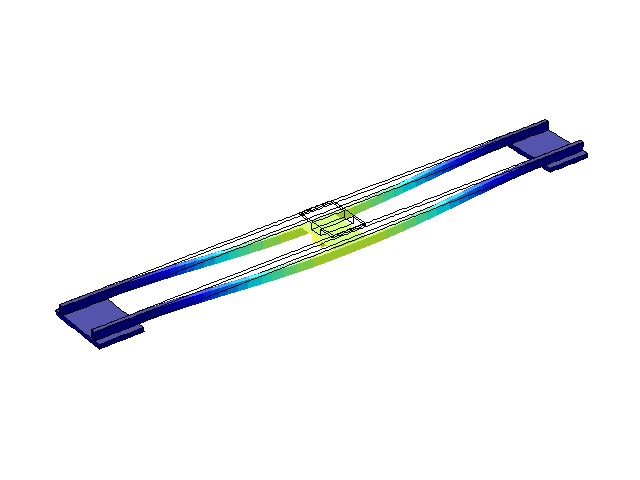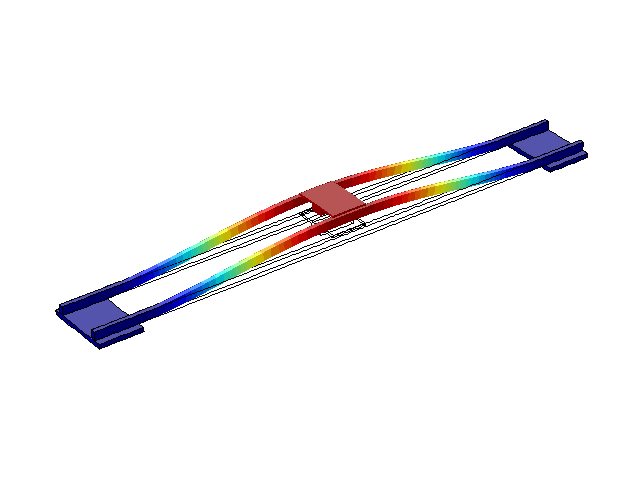
Рисунок 4 – Режим власних коливань моста при частоті f=1,76 Гц
(анімація: 24 кадри, нескінченне повторення, 275 килобайти)
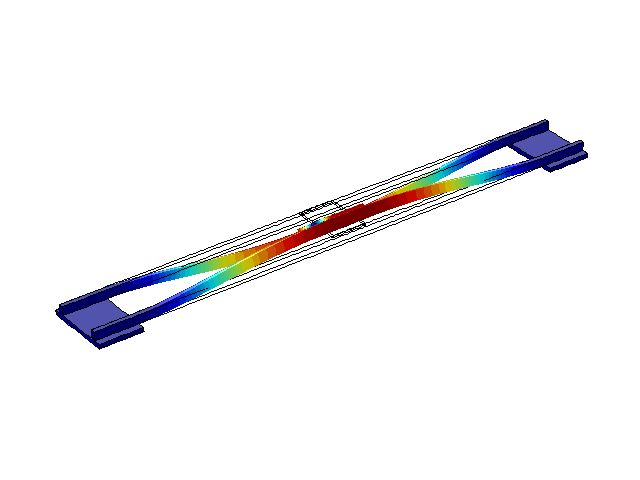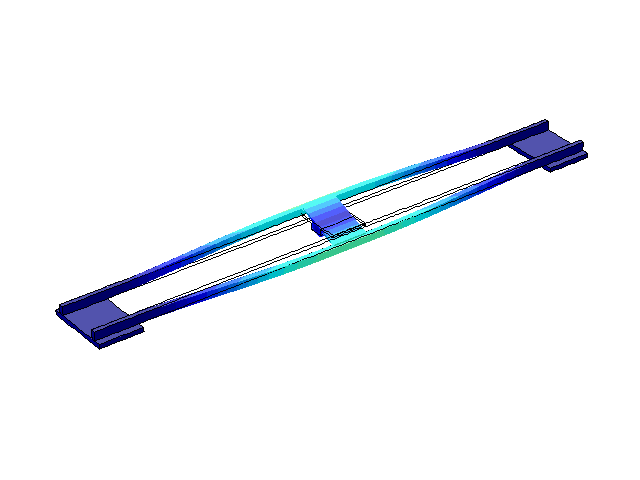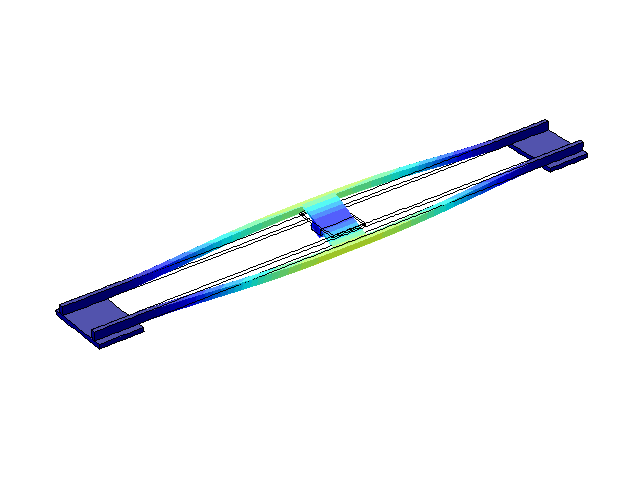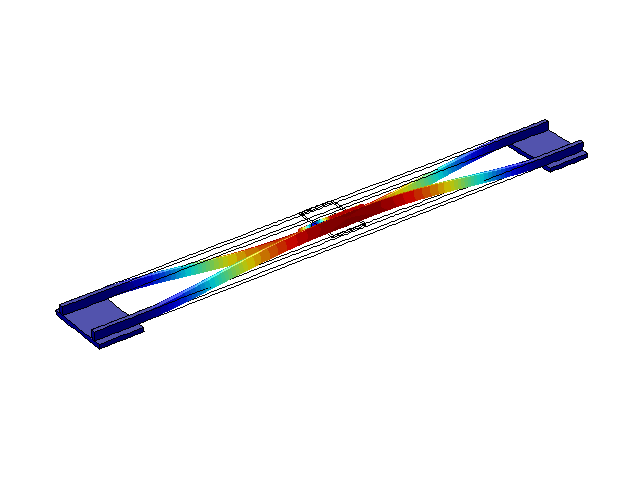
Рисунок 5 – Режим власних коливань моста при частоті f=3,31 Гц
(анімація: 24 кадри, нескінченне повторення, 289 килобайти)
4.3 Отримання графіків перехідних процесів
Графіки перехідних процесів при переміщенні мосту отримані зі спрощенням, що приводні моменти двигунів утворюють зусилля, яке рівномірно розподіляється по площині кінцевих граней моделі [7].
Зусилля, прикладене до моста, відповідає розгону до швидкості 0.5 м/с за 1 с і аналогічному гальмуванню через 7 с руху на усталеній швидкості. Результати моделювання показали, що за умови розташування візка у центральній точці моста, швидкості й переміщення його крайніх точок є абсолютно рівними.
Графіки зміни швидкості крайніх точок моста v1 і візка v2, а також максимальної деформації моста у напрямку його руху Δs2, яка виміряється у його центральній точці, наведені на рис. 6. Із графіків видно, що в обох крайніх точках мають місце недемпфовані коливання, при чому амплітуда коливань швидкості досягає значення 0.1 м/с.
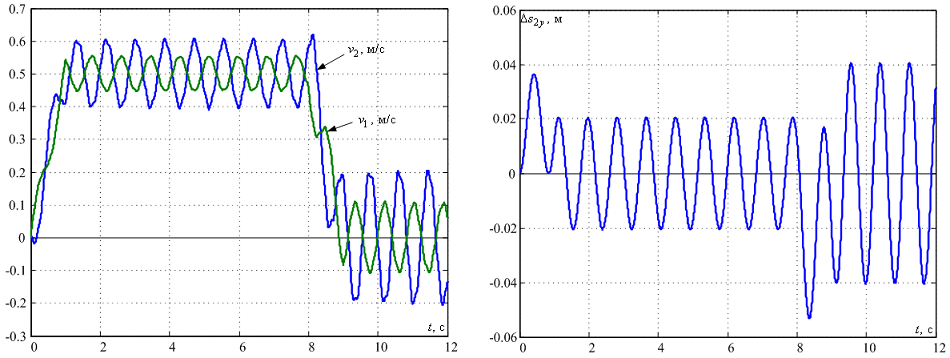
Рисунок 6 – Перехідні процеси руху пружної конструкції мостового крану
Вочевидь, суттєвий вплив на перехідні процеси має лише одна гармонічна складова, яка відповідає режиму власних коливань з частотою f=1.18 Гц, як це показано на рис. 3. Графік перехідних процесів за швидкістю свідчить, що в спектрі коливань присутня як мінімум ще одна гармонійна складова, проте її амплітуда є значно меншою за основну, а тому її впливом можна знехтувати. Тому вважаємо, що процес пружних коливань із достатнім ступенем точності описується за допомогою консервативної ланки, передавальна функція якої має вигляд:
Такий опис відповідає поведінці багатомасової електромеханічної системи, яку приймемо за основу при створенні спрощеної математичної моделі.
4.4 Математичний опис лінійної двомасової системи мостового крану
У найбільш загальному випадку міст необхідно розглядати як тримасову електромеханічну систему [4], кінематичну схему якої наведено на рис. 7а.
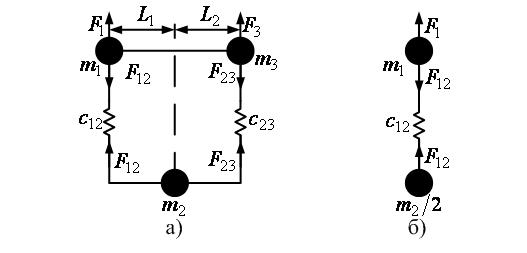
Рисунок 7 – Кінематичні моделі моста
В такому випадку міст умовно представлений у вигляді трьох зосереджених мас – крайніх точок m1 і m3, зв’язаними пружними зв’язками з коефіцієнтами жорсткості c12 й c23 с точкой m2, в якій знаходиться візок.
Якщо візок розташовано у середній точці моста (L1=L2), то і коефіцієнти жорсткості мають бути однаковими. Якщо при цьому дорівнюють одна одній маси, зосереджені на кінцях мосту, а також прикладені до них сили, кінематичну схему моста можна спростити до двомасової, залишивши лише одну з опор (крайніх точок) і центральну точку, зменшивши її масу вдвічі, як це показано на рис. 7б. Математичний опис такої системи матиме такий вигляд:
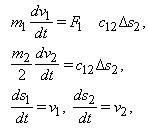
де F1 – сила, прикладена до першої маси, F12 – пружна сила, Δs2=s1-s2 – величина пружної деформації.
При відомих значеннях зосереджених мас і сталої часу пружних коливань двомасової системи T12=1/2πf коефіцієнт жорсткості можна розрахувати за формулою:
Отже одним із головних питань при моделюванні у даному випадку є вибір величин зосереджених мас.
В результаті досліджень лінійної моделі встановлено, що при зміні розподілу маси моста між опорами і місцем знаходження візка бажана частота пружних коливань досягається при різних амплітудах сигналів v1 и v2. Найкращий збіг цих амплітуд з результатами, отриманими у пакеті Comsol, забезпечується при розрахунку зосереджених мас за формулами:
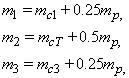
де mc1,3 – маси першої і другої опор відповідно, які включають масу коліс, електроприводів і кінцевих балок, mh – розподілена маса головних балок моста, mcT – зосереджена маса візка. Такий розподіл мас співпадає з рекомендаціями, наведеними в [1], хоча в деяких джерелах пропонується масу моста розподіляти рівномірно між опорами, без середньої точки [2].
Результати моделювання лінійної двомасової системи з рекомендованими параметрами наведено на рис. 8, з якого видно, що отримана модель достатньо точно відображує процес переміщення конструкції, отриманий в пакеті Comsol Mutiphysics [10]. При цьому амплітуда коливань швидкості другої маси є дещо меншою у порівнянні з графіками рис. 6. Проте ці відмінності є несуттєвими, а тому для цієї моделі проведемо синтез регулятора для гасіння коливань.
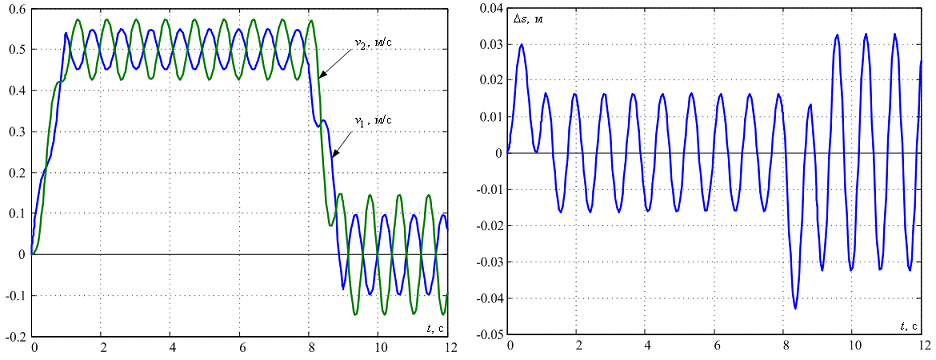
Рисунок 8 – Перехідні процеси в лінеаризованій системі
4.5 Синтез регулятора для гасіння коливань
Одним із можливих варіантів є застосування регулятора з лінійним зворотним зв’язком за повним вектором стану системи, структурна схема якої наведена на рис. 9 [9].
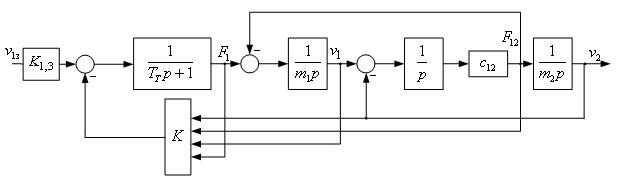
Рисунок 9 – Структурна схема двомасової системи з регулятором
Контур регулювання струму представляємо у вигляді аперіодичної ланки зі сталою часу TT=0.001 с. Впливом перехресних зв’язків для електроприводів змінного струму і внутрішнього зворотного зв’язку за ЕРС обертання двигуна нехтуємо. Тоді отримаємо такий вектор стану системи:
Коефіцієнти модального регулятора розраховуємо за коефіцієнтами αi бажаного характеристичного полінома, які визначають динаміку системи. В результаті синтезу отримано такі вирази для коефіцієнтів регулятора стану:
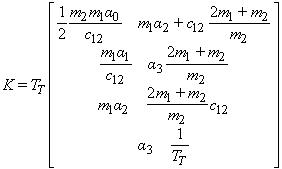
Результати моделювання системи з таким регулятором при використанні розподілу Бесселя із середньогеометричним коренем Ω0=1/(8TT), наведено на рис. 10. Бачимо, що коливання у системі відсутні, а максимальне значення відхилення середньої точки моста зменшилося у порівнянні з результатами, наведеними на рис. 8 майже удвічі.
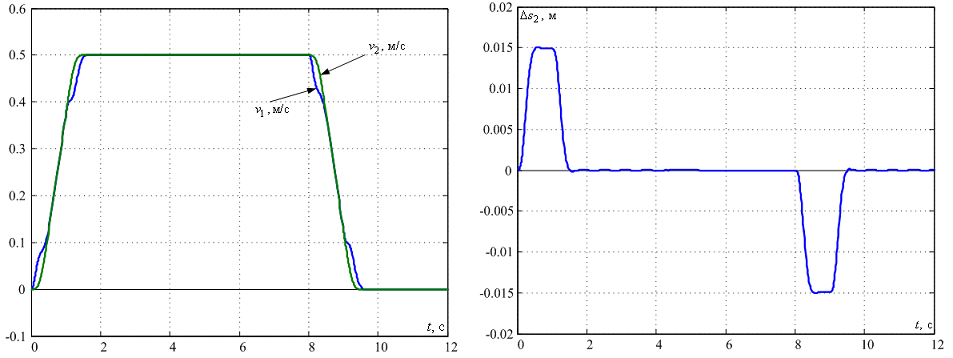
Рисунок 10 – Перехідні процеси в лінійній моделі з регулятором стану
Слід враховувати, що лінійна модель є наближеною, а тому необхідно перевіряти адекватність отриманих результатів на моделі з розподіленими параметрами [6].
4.6 Перевірка результатів на моделі з розподіленими параметрами
Для цього прикладемо до моделі моста в програмному пакеті Comsol лінійну силу, отриману в системі з модальним регулятором на виході контуру струму. Результати моделювання наведено на рис. 11.
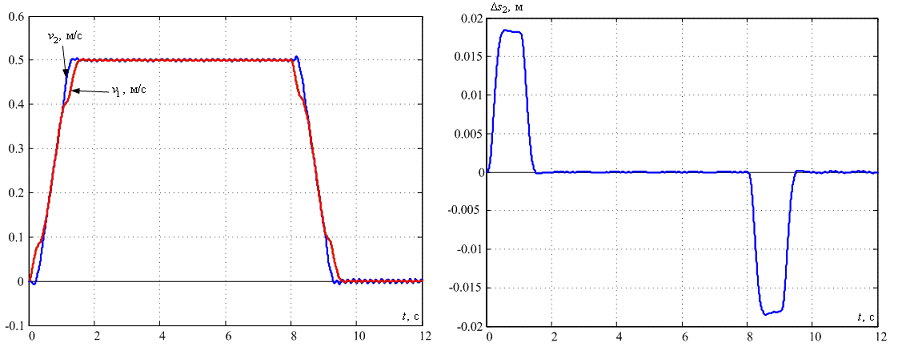
Рисунок 11 – Перехідні процеси в моделі з розподіленими параметрами при подачі на неї вихідного сигналу контуру струму в системі з регулятором стану
Бачимо, що низькочастотні пружні коливання повністю гасяться. При цьому залишаються незначні коливання більш високої частоти, не враховані у лінійній моделі. Тим не менш, результати моделювання збігаються з отриманими на лінійній моделі, що підтверджує її адекватність.
Подальші дослідження, виконані в Comsol, показали, що при фіксації візка в інших точках мосту характер пружних коливань мосту істотно змінюється: з’являються додаткові частоти, що змінюються в широкому діапазоні. Це робить неможливим застосування синтезованого модального регулятора при великому діапазоні переміщень візка. Для синтезу адаптивної системи управління можна використовувати лінійну модель мосту на підставі тримасовой кінематичної схеми рис. 7а, у якій зміна положення візка враховується зміною коефіцієнтів пружності й розподілу мас.
У цьому випадку перспективним представляється розрахунок декількох модальних регуляторів, що відповідають різним положенням візка, й плавний перехід від одного настроювання до іншого за допомогою нечіткого регулятора типу Сугено [5].
Висновки
Отримано комп’ютерну модель конструкції мостового крану у програмному пакеті Comsol Multiphysics, яка враховує розподіл маси і пружності по її довжині і дозволяє досліджувати її пружні коливання. На основі отриманих графіків перехідних процесів було створено спрощену лінеаризовану модель, яка дозволяє проводити синтез регуляторів для гасіння пружних коливань конструкції.
Найбільш суттєві висновки і рекомендації полягають у наступному:
- Аналіз пружних властивостей механічних конструкцій зручно проводити за допомогою спеціалізованого програмного забезпечення, яке використовує метод кінцевих елементів.
- При переміщенні моста суттєвий вплив на його рух здійснює лише одна гармонічна складова пружних коливань.
- За умови, коли нерухомий візок знаходиться у центральній точці моста, динамічні властивості конструкції моста можна представити у вигляді двомасовой електромеханічної системи.
- Використання модального регулятора дозволяє ефективно гасити пружні коливання конструкції моста, якщо є можливість отримати інформацію про усі наявні змінні стан у будь-який момент часу.
Примітка. Під час написання цього реферату дипломна робота знаходиться ще на стадії виконання, тому наведений реферат містить наявні на момент складання іспиту з дисципліни «Інтернет-технології» інформацію. Кінцевий строк виконання магістерської роботи й дата захисту диплома – січень 2014 року.
Перелік посилань
- Будіков Л.Я. Багатопараметричний аналіз динаміки вантажопідйомних кранів мостового типу: Монографія. – Луганськ, вид-во СНУ ім. В.Даля, вид. 2-е, 2003. – 210 с.
- Макурин А.В., Морозов Д.И. Динамика продольного перемещения мостового крана с учетом упругости элементов конструкции // Електротехнічні та комп’ютерні системи. – 2011. – №3(79). – С. 167-169.
- A. Buch. Optimale Bewegungssteuerung von schwingungsfahigen mechatronischen Systemen mit zwei Freiheitsgraden am Beispiel eines Krans mit Pendelnder Last und elastischer Mechanik – Magdeburg, 1999. – 250 S.
- B. Jerman. An enhanced mathematical model for investigating the dynamic loading of a slewing crane [Электронный ресурс]: / B. Jerman. – Электрон. текст. дан. – Slovenia: 2006. – Режим доступа: http://pic.sagepub.com/content/220/4/421
- C.Y. Chang. The switching algorithm for the control of overhead crane [Электронный ресурс]: / C.Y. Chang. – Электрон. текст. дан. – China: 2006. – Режим доступа: http://link.springer.com/article/10.1007%2Fs00521-006-0036-z
- E. Reynders. Reference-based combined deterministic-stochastic subspace identification for experimental and operational modal analysis [Электронный ресурс]: / E. Reynders, G. De Roeck. – Электрон. текст. дан. – Belgium: 2008. – Режим доступа: http://www.sciencedirect.com/science/article/pii/S0888327007001823
- F.L. Chernousko. Control of elastic systems by bounded distributed forces [Электронный ресурс]: / F.L. Chernousko. – Электрон. текст. дан. – Russia: 1996. – Режим доступа: http://www.sciencedirect.com/science/article/pii/009630039600001X
- K.A.F. Moustafa. Modelling and control of overhead cranes with flexible variable-length cable by finite element method [Электронный ресурс]: / K.A.F. Moustafa, E.H. Gad, A.M.A. El-Moneer, M.I.S. Ismail. – Электрон. текст. дан. – Egypt: 2005. – Режим доступа: http://tim.sagepub.com/content/27/1/1.abstract
- N. Uchiyama. Robust control of rotary crane by partial-state feedback with integrator [Электронный ресурс]: / N. Uchiyama. – Электрон. текст. дан. – Japan: 2009. – Режим доступа: http://www.sciencedirect.com/science/article/pii/S0957415809001500
- 10. Y. Sakawa. Nonlinear model and linear robust control of overhead traveling cranes [Электронный ресурс]: / Y. Sakawa, H. Sano. – Электрон. текст. дан. – Japan: 1997. – Режим доступа: http://www.sciencedirect.com/science/article/pii/S0362546X97860415
