DonNTU   Masters' portal

Abstract

Content

1. The general formulation of the problem and its relevance

Traditional in design of digital control systems is a hypothesis about the fact that discrete period is constant, and it does not change during operation of the system. But modern technology is the implementation of automation systems based on the use of advanced telecommunication networks such as DeviceNet, Ethernet, FireWire and others that connect sensors and actuators with controllers, that is, between the controller (control part of the system) and subject to the sensors and actuators is a telecommunication network, the resources of which are also using other controllers. In such networks, conflicts may arise, which lead to the fact that the controller receives the information about the state of the object does not at discrete instants of time and a random time shift with respect to discrete time which was acceptable during the system design. Uncertainty with a packet transmission network information, wherein packets may be lost or corrupted, also leads to an increase in the interval between samples. The second reason, which can be regarded as a random change of sampling period, is to delay the production of the desired sensor controller information, because the information is there complex calculations that can last for a while. Image discrete period adversely affects the quality control system, and may cause loss of its stability. This is a problem in recent years more and more attracted the attention of researchers working in the field of control systems.

2. Overview of research and development

The growing interest in network management systems indicates a large number of publications devoted to the search counteract uncertainty telecommunications network with a view to ensuring the sustainability and quality management systems [3,4,5,6]. Among all the different publications the most common approach to the analysis of systems with variable period of quantization robot [1], in which the proposed use of the Kolmogorov-Feller about the probability density of the phase coordinates. But in recent years there has been an opportunity to study the stability of the network of automatic control systems for discrete random change of the period on the basis of the theory of robust systems. Sampling period is considered as a parameter whose variation leads to a parametric uncertainty of the transfer functions of a digital controller (additive or multiplicative). If we consider the conditions of robust stability of the system, it may be an estimate of the maximum variation sampling period for which the system remains stable.

3. Statement of the research problem

To make the task of studying the dynamics of digital systems with variable sampling period reduced to the study of robust stability of the system, you need to consider and address the following tasks:

  1. determine the mechanism of the influence of a variable period of discretion to change the parameters of the transfer function of the controller or the control object (in the discrete representation of it) in the transition from the z-to the s-plane;
  2. based on the model of a system with parametric uncertainty to evaluate the changes of the valid period of the discrete while maintaining the stability of the system.

4. Solution of the problem and current results of the research

The following is considered a network system of automatic control, the structure of which is shown in Figure 1.

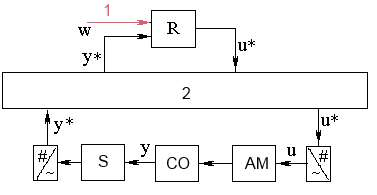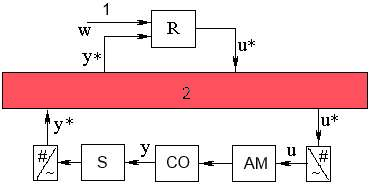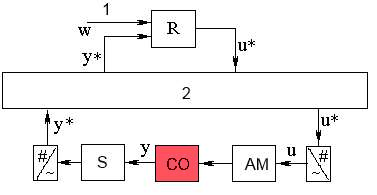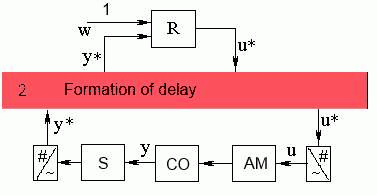
Передача информации в сетевой САУ

Figure 1 – Information transfer in network CAS. 1 – task, 2 – NCS, R – regulator, CO – control object, AM – actuating mechanism, S– sensor.
(animation: 7 frames, 1 s delay, size 88,2 kB, an unlimited number of repetitions, made with MP Gif Animator)

Regulator, which is implemented on a microcontroller or a dedicated computer, characterized by its z-transfer function for the system design which has been determined for a particular sampling period .Telecommunication network may delay the transmission of information from the sensor to the controller at the time ΔT. With the "point of view" of the analog object it will mean a change of the transfer function of the regulator. Change the transfer function of the controller is possible (see [2]) to take into account in the process of converting z-transfer function of the regulator in its s-equivalent, putting it , where ΔT - current sampling period.

Suppose, for example, for stabilizing an object with the transfer function r2 is calculated from the controller r3. For the period r4 derived from the discrete z-transfer function of the controller r5. If you change the sampling period, the regulator receives a signal from the sensor as a result of collisions on the network less often than r6, the general dynamics of the controller becomes different at the nominal sampling period. Changing dynamics of the regulator under constant coefficients of its transfer function can be accounted for T by setting the bilinear transformation r1: at various T get the transfer function of the controller r7, is directly dependent on the period of discrete nature. For the regulator, which is seen in the example of this relationship is as follows:

r8                                                                                    (1)

After appropriate transformations, we obtain a block diagram of the controller (Fig. 2), which is in the division block T, on that allows you to take into account the change in the period in analysis of discrete closed-loop control system with variable sampling period.

ris2


Figure 2 - Block diagram of the controller with a block division.

r9

r10

r11

   

On the basis of Figure 2 for T the (upper limit T can be estimated taking into account the technical characteristics of the telecommunications network), you can calculate the additive error (uncertainty) Δа (jω) to the regulator, r12 - the rate that is required to assess the stability of the closed system. Figure 3a shows the logarithmic frequency response of the controller for the nominal sampling period r6 and sampling period T, which is two times greater than the nominal. Fig. 3b - the additive error of the transfer function of the regulator (1) when the sampling period doubled:

r14.

ris3a

а)

ris3b

b)

Figure 3 - The logarithmic performance of the controller:

a) for different sampling period; b) an additive error.

   

Conclusions

The task of analyzing the influence of a variable period of discretion on the stability of the closed system can be reduced to the problem of estimating the robust stability. Discrete change in the period leading to the fact that changes the dynamics of its own controller, ie changes its transfer function. The deviation from the nominal transfer function of the controller is represented as an additive error (uncertainty), which can be calculated by using the bilinear transformation.

Using linear fractional transformation lft to represent discrete variable period allows to evaluate the stability of the closed-loop system when certain increase or calculate its allowable value while maintaining the stability of the system. In case the controller structure comprises two or more blocks dividing by T, each of them must provide the structure and merge dai into a single multi-dimensional blocks with diagonal block elements dai. With respect to this last part of the block is considered as a multi-dimensional closed system, for which the stability condition must be satisfied r41.

The results of this study can be used to study the requirements for bandwidth, and for determining the maximum allowable delay in the transmission of data from sensors to the controller and from a mechanism for executing automatic control network.

References

1. Артемьев В.М.,Ивановский А.В. Дискретные системы управления со случайным периодом квантования. – М.: Энергоатомиздат, 1986. - 96с.

2. Grobe M. Ein Ansatz zur Stabilitätsuntersuchung von Systemen mit nicht konstanter Abtastung : 2009 - 144.Access mode:http://rzbl04.biblio.etc.tu-bs.de:8080/docportal/servlets/MCRFileNodeServlet/DocPortal_derivate_00008028/Druckversion_20091203.pdf

3. G.C. Walsh and Y. Hong and L.G. Bushnell. Stability Analysis of Networked Control Systems. IEEE Transactions on Control Systems Technology, 10(3):438–46, May 2002.

4. Ray A, Galevi Y. Intergrated communication and control systems: Part II – design considerations. J Dyn Syst Measurement Contr 1988; 110: 374–381.

5. J.K. Yook, M.Tilbury, and N.R. Soparkar. Trading Computation for Bandwidth: Reducing Communication in Distributed Control Systems Using State Estimators. IEEE Transactions on Control Systems Technology, 10(4):503.

6. W. Zhang and M.S. Branicky and S.M. Phillips. Stability of Networked Control Systems. IEEE Control System Magazine, 21(1):84–99, February 2001.

7. P. Seiler and R. Sengupta. Analysis of Communication Losses in Vehicle Control Problems.Proceedings of the American Control Confrence, p.1491–1496, June 2001.