ДонНТУ  Портал магистров

Реферат по теме выпускной работы

Содержание

1. Общая постановка задачи и её актуальность

Традиционной при проектировании цифровых систем управления является гипотеза про то, что период дискретности является постоянным, и он не меняется во время эксплуатации системы. Но современная технология реализации систем автоматики базируется на использовании развитых телекомуникационных сетей, таких как DeviceNet, Ethernet, FireWire и других, которые связывают датчики и исполнительные механизмы с контроллерами, то есть между контроллером (управляющая часть системы) и объектом с датчиками и исполнительными механизмами находится телекомуникационная сеть, ресурсы которой используют также другие контроллеры. Этот тип системы имеет преимущество большей гибкости относительно традиционных систем управления. Кроме того, это допускает уменьшенное проводное соединение, а также более низкую стоимость установки. Это также разрешает большую быстроту в диагнозе и правилах технического обслуживания. Типичные примеры: распределенные промышленные САУ/АСУ, интеллектуальные транспортные системы, спутниковые кластеры и групповые маневры, массивы мобильных датчиков, несколько автономных мобильных роботов, гибкие децентрализованные производственные систем большого масштаба, организация полета группы беспилотных летательных аппаратов, многоагентные системы, продвинутые сети летательных и космических аппаратов и т.д. Коммуникационная сеть в обратной связи делает анализ и проектирование сетевого комплекса систем управления довольно сложным. Инструменты и методы, разработанные в стандартной теории управления, недостаточны для этого анализа и должны быть изменены для учитывания дополнительной сложности. Одним из ключевых вопросов, возникающих при применении CCУ являются ненадежные каналы передачи из-за ограниченной полосы пропускания и большого количества данных, передаваемых по одному каналу. Так как сеть связана с системами управления, задержки вызванные сетью всегда присущи ССУ и при этом всегда влияют на ее работу.В таких сетях могут возникать коллизии, которые приводять к тому, что контроллер получает необходимую информацию про состояние объекта не в дискретные равноотдаленные моменты времени, а со случайным сдвигом во времени относительно того периода дискретности, который был приемлимым во время проектирования системы. Неопределенность сети с пакетной передачей информации, где пакеты могут быть потеряны или испорчены, также ведет к увеличению промежутка времени между отсчетами. Второй причиной, которая может быть расценена как случайная смена периода дискретности, является задержка датчиком изготовления нужной контроллеру информации, потому что эта информация возникает вледствие сложных расчетов, которые могут длиться некоторое время. Увеличение периода дискретности негативно влияет на качество системы управления и может быть причиной потери её устойчивости. Именно эта проблема в последние годы все больше привлекает внимание исследователей, которые работают в области систем управления.

2. Обзор исследований и разработок

На растущий интерес к сетевым системам управления указывает большое количество публикаций, посвященных поиску противодействия неопределенности телекоммуникационной сети с целью гарантированного обеспечения устойчивости и качества системы управления [3,4,5,6]. Среди всех публикаций отличается наиболее общим подходом к анализу систем с переменным периодом квантования робота [1], в которой предложено использовать уравнения Колмогорова-Феллера по поводу плотности вероятности фазовых координат. Но в последние годы появилась возможность провести исследование устойчивости сетевых систем автоматического управления при случайной смене периода дискретности на основании теории робастных систем. Период дискретизации рассматривается как параметр, изменение которого ведет к параметрической неопределенности передаточной функции цифрового регулятора (аддитивной или мультипликативной). Если рассмотреть условия робастной устойчивости системы, то может быть получена оценка максимального изменения периода дискретности, при котором система остается устойчивой.

3. Постановка задачи исследования

Для того, чтобы задачу исследования динамики цифровой системы с переменным периодом дискретности свести к задаче исследования робастной устойчивости системы, необходимо рассмотреть и решить следующие задачи:

  1. Выяснить механизм влияния переменного периода дискретности на изменение параметров передаточной функции регулятора или объекта управления (в дискретном его представлении) при переходе от z- к s-плоскости;
  2. На основании модели системы с параметрической неопределенностью провести оценку границы допустимого изменения периода дискретности при сохранении устойчивости системы.

4. Решение задачи и текущие результаты исследования

В следующем рассматривается сетевая система автоматического управления, структура которой приведена на рис.1.

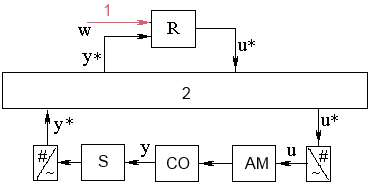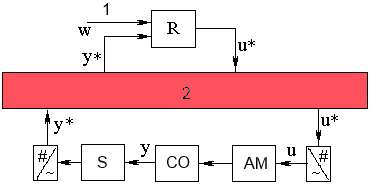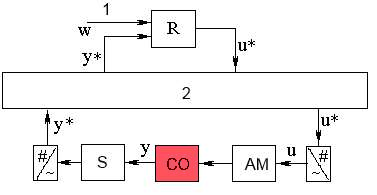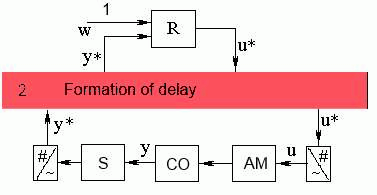
Передача информации в сетевой САУ

Рисунок 1 – Передача информации в сетевой САУ. 1 – задание, 2 – телекоммуникационная сеть, R – регулятор, СO – объект управления, АM – исполнительный механизм, S – датчик.
(анимация: 7 кадров, задержка между кадрами 1 с, количество циклов повторения — бесконечное, размер 88,2 килобайт, создана при помощи MP Gif Animator)

Регулятор, который является реализованным на микроконтроллере или специализированной ЭВМ, характеризуется своей z-передаточной функцией, которая при проектировании системы была определена для определенного периода дискретности . Телекоммуникационная сеть может задержать передачу информации от датчика к регулятору на время . С «точки зрения» аналогового объекта это будет означать изменение передаточной функции регулятора. Изменение передаточной функции регулятора можно (см. [2]) учесть в процессе преобразования z-передаточной функции регулятора в его s-эквивалента, подставляя в нее ,где - актуальный период дискретности.

   

Пусть, например, для стабилизации объекта с передаточной функцией r2 является рассчитанным регулятор с r3. Для периода дискретности r4 с получена z-передаточная функция регулятора r5. При изменении периода дискретности, когда регулятор получает сигнал от датчика вследствие коллизии в сети реже чем r6, общая динамика регулятора становится отличной при номинальном периоде дискретности. Изменение динамики регулятора при неизменных коэффициентах его передаточной функции можно учесть через параметр T билинейной преобразования r1: при различных T получают передаточную функцию регулятора r7, непосредственно зависят от периода дискретности. Для регулятора, который рассматривается в примере, эта зависимость имеет следующий вид:

r8                                                                                    (1)

После соответствующих преобразований получим структурную схему регулятора (рис.2), в составе которого есть блок деления на T, который позволяет учесть изменение периода дискретности при анализе свойств замкнутой системы управления с переменным периодом дискретности.

ris2


Рисунок 2 – Структурная схема регулятора с блоком деления

r9

r10

r11

   

На основании рис.2 для T (верхняя граница может быть оценена с учетом технических характеристик телекоммуникационной сети) можно рассчитать аддитивную ошибку (неопределенность) ∆а (jω) регулятору, r12- норма которой требуется для оценки устойчивости замкнутой системы.

На рис.3а показаны логарифмические частотные характеристики регулятора для номинального периода дискретности r6 и для периода дискретности T, который в два раза больше чем номинальный. На рис. 3б - аддитивная погрешность определения передаточной функции регулятора (1) при изменении периода дискретности вдвое:

r14.

ris3a

а)

ris3b

б)

Рисунок 3 – Логарифмические характеристики регулятора:

а) для разных периодов дискретности; б) аддитивная погрешность.

    Рассмотрим систему автоматического управления (рис.4) с номинальной моделью объекта управления W (s) и регулятора WR(s), передаточная функция которого определена с аддитивной погрешностью Δa(jω).

а)ris4aб) ris4bв) ris4c

Рисунок 4 – а) Система с аддитивной неопределенностью передаточной функции регулятора

                                                  

б) Представление системы в форме М,∆-структуры

                                                   

в) Матричные уравнения к М,∆-структуре


    Пусть входными сигналами будут сигналы w и v, а выходными - z и y, т.е. систему с параметрической или структурной неопределенностью можно представить как двухмерную (рис. 4б) и определить передаточные функции r15 , r16, r17, r18.
    С учетом обозначений на рис.4a) легко получить соответствующие передаточные функции, а именно:

r19; r20;

r21; r22.

    С другой стороны на основании матричного уравнения (рис. 4в) можно записать следующие соотношения, учитывая, что r23:

r24

    Решением уравнений относительно y и w является соотношение (2)

r27,                                                                            (2)

отражающее передаточную функцию замкнутой системы с учетом аддитивной неопределенности передаточной функции регулятора. Для сокращения записи последней формулы и для упрощения представления различных робастных систем используется запись r28 , которая соответствует «верхнему» линейному дробному преобразованию r29 (upper).

На основании уравнения (2) можно сделать важные выводы относительно устойчивости системы автоматического управления, в которой передаточная функция регулятора определена с параметрическими или структурными погрешностями (независимо от причин, вызвавших появление аддитивной или мультипликативной погрешности).

Вывод 1. Если период дискретности не изменяется во время эксплуатации системы, то параметрическая или структурная погрешности определения передаточной функции регулятора относительно его номинальной модели отсутствуют (r30) [7]. В таком случае уравнение (2) устанавливает зависимость выхода системы от входа, которая равна передаточной функции r32 замкнутой системы. Характерным уравнением является r31, что соответствует устойчивой системе вследствие разумного выбора регулятора.

    Вывод 2. При наличии аддитивной погрешности (r30) устойчивость системы определяется составляющей r33, которой соответствует дополнительный контур с положительной обратной связью. Характеристическое уравнение для оценки устойчивости имеет вид 

r34.                                                                                               (3)

Передаточную функцию r35 можно представить в виде произведения передаточной функции объекта r36 и чувствительности номинальной системы r37, т.е. r38. В частотной области характеристическое уравнение (3) для обеспечения устойчивости системы превращается в выражение

r39для r40.                                                                        (4)    

    Учитывая то, что абсолютная величина  r43 является ограниченной сверху, то есть r44, критерий устойчивости (4) можно представить в форме (5):

r45,                                                                             (5)

или строже 

r46.                                                                                 (6)


Последнее выражение по определениям соответствует r12 - норме : r47 , поэтому критерием устойчивости является также

r48 .                                                                                 (7)

На основании, например, критерия устойчивости (7) легко проверить, будет ли замкнутая система устойчивой, если период дискретности станет вдвое большим. Так, рассмотрев логарифмическую частотную характеристику r49, которая приведена на рис. 5, можно сделать вывод, что система остается устойчивой, потому что r50 <r40 .

ris5


Рисунок 5 – Значение критерия устойчивости (7)

Структура регулятора может быть сложнее и содержать два и больше блоков деления на T, (например в ПИД-регуляторе с параллельной структурой). В таком случае необходимо каждый блок деления заменять на эквивалентную структуру, блоки dai  объединяются в один многомерный блок с диагональными элементами dai. Относительно этого блока последняя часть системи рассматривается как многомерная замкнутая система. Очевидно, что для устойчивости многомерной системы также должно выполняться условие r41, где r51 - передаточная функция от i-го выхода блока dai к j-му входу.

Выводы

    Задачу анализа влияния переменного периода дискретности на устойчивость замкнутой системы удается свести к задаче оценки робастной устойчивости. Изменение периода дискретности ведет к тому, что изменяется собственная динамика регулятора, т.е. изменяется его передаточная функция. Отклонение от номинальной передаточной функции регулятора представляется как аддитивная погрешность (неопределенность), которую можно рассчитать путем использования билинейной преобразования. С использованием критериев проверяется устойчивость системы автоматического управления.

    Использование линейного дробного преобразования lft для представления переменного периода дискретности позволяет оценивать устойчивость замкнутой системы при его определенном увеличении или рассчитать его допустимую величину при сохранении устойчивости системы. В случае, если структура регулятора содержит два и более блоков деления на T, необходимо каждый из них представить структурой, и объединить блоки dai в один многомерный блок с диагональными элементами dai. Относительно этого блока последняя часть системы рассматривается как многомерная замкнутая система, для устойчивости которой должно выполняться условие r41.

    Результаты данного исследования можно применять для обоснования требований к пропускной способности сети, а также для определения максимально допустимой задержки в передаче информации от датчиков к регулятору и от него к исполняющему механизму в сетевых системах автоматического управления.

Список источников

  1. Артемьев В.М., Ивановский А.В. Дискретные системы управления со случайным периодом квантования. – М.: Энергоатомиздат, 1986. - 96с.
  2. Grobe M. Ein Ansatz zur Stabilitätsuntersuchung von Systemen mit nicht konstanter Abtastung : 2009 - 144. Режим доступа: http://rzbl04.biblio.etc.tu-bs.de:8080/docportal/servlets/MCRFileNodeServlet/DocPortal_derivate_00008028/Druckversion_20091203.pdf
  3. G.C. Walsh and Y. Hong and L.G. Bushnell. Stability Analysis of Networked Control Systems. IEEE Transactions on Control Systems Technology, 10(3):438–46, May 2002.
  4. Ray A, Galevi Y. Intergrated communication and control systems: Part II – design considerations. J Dyn Syst Measurement Contr 1988; 110: 374–381.
  5. J.K. Yook, M.Tilbury, and N.R. Soparkar. Trading Computation for Bandwidth: Reducing Communication in Distributed Control Systems Using State Estimators. IEEE Transactions on Control Systems Technology, 10(4):503.
  6. W. Zhang and M.S. Branicky and S.M. Phillips. Stability of Networked Control Systems. IEEE Control System Magazine, 21(1):84–99, February 2001.
  7. P. Seiler and R. Sengupta. Analysis of Communication Losses in Vehicle Control Problems.Proceedings of the American Control Confrence, p.1491–1496, June 2001.