СТАБИЛИЗАЦИЯ ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ИЗМЕНЯЮЩЕЙСЯ ВО ВРЕМЕНИ ЗАДЕРЖКОЙ
Авторы: Никитенко Д.Г., Хорхордин А.В..
Источник: Автоматизація технологічних об’єктів та процесів. Збірник наукових праць / Матеріали ХIІІ міжнародної науково-технічної конференції
аспірантів і студентів Пошук молодих — Донецьк, ДонНТУ — 2013, с. 309-313.
Исследуется устойчивость дискретных систем с нестационарным
запаздыванием. Разработаны новые зависимые от задержки критерии
устойчивости, которые зависят от минимальной и максимальной границы
задержки. Первоначальный анализ приводит к критерию в зависимости от
неравенства с участием определенных матриц, которые могут быть выбраны
произвольно. Тщательно выбирая их, чтобы отразить соответствующие
отношения между состояниями в разное время, получен более строгий
критерий. Кроме того, новые результаты для зависимых от задержки
робастных систем с изменяющимися во времени задержкой предоставляются
на основе линейного матричного неравенств (ЛМН). Так как условия,
полученные для существования допустимых регуляторов не выражаются с
помощью строгих условий ЛМН, линеаризация используется для поиска
подходящего контроллера. Наконец, полученные результаты, в том числе
анализ устойчивости, статическая стабилизация обратной связью по выходу
и динамическая стабилизации обратной связью по выходу расширяется на
дискретные системы с запаздыванием, имеющие неопределенные, но
ограниченные по норме параметры.
Временные
задержки часто возникают в системах управления и часто являются
источником нестабильности и колебаний в таких системах. Оценка и
контроль устойчивости таких систем с запаздыванием имеют теоретическое
и практическое значение. Повышенное внимание было уделено проблеме
обратной связи для стабилизации систем с задержкой по состоянию.
Большинство полученных результатов были получены с использованием
независимых от задержки подходов. Так как время задержки не принимается
во внимание при использовании этих подходов к разработке регуляторов,
результат получается, как правило, более консервативный, чем при
использовании подхода с учетом задержки. Тем не менее, более ранние
методы с зависимостью от задержки для систем с нестационарными
задержками в основном применяются к непрерывным системам. Сравнительно
мало работ рассматривает изменяющиеся во времени задержки в случае
систем с дискретным временем. Недавно была исследована стабилизация
системы по обратной связи по выходу при учете зависмости от задержки с
изменяющимися во времени задержками по состоянию. Новое условие
устойчивости было предложено, которое зависит от пределов
изменения задержки. Их результаты основаны на неравенстве со скалярным
произведением двух векторов доказанном Муном. Для заданного состояния  , где
, где  - дискретное временем, с зависящей от времени задержкой
- дискретное временем, с зависящей от времени задержкой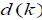 , это неравенство, как правило, используется для оценки ограничений на
взвешенное векторное произведение между
, это неравенство, как правило, используется для оценки ограничений на
взвешенное векторное произведение между  и разностью
и разностью 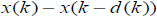 , необходимая для анализа устойчивости в зависимости от задержки.
Использование этого неравенства приводит к консерватизму в полученных
условий устойчивости зависимых от задержки.
, необходимая для анализа устойчивости в зависимости от задержки.
Использование этого неравенства приводит к консерватизму в полученных
условий устойчивости зависимых от задержки.
Эта статья представляет собой
новый подход к созданию более строгого критерия устойчивости для
нестационарных систем с запаздыванием зависимого от задержки, используя
отношения между всеми состояниями системы  , не требуя необходимости преобразования какой-либо модели системы.
Начальный критерий находится на основе неравенства, включающего
различные матриц, которые могут быть свободно выбраны, и улучшенный
критерий затем находится тщательно выбирая эти матрицы с учетом
корреляции между состояниями системы при различных задержках.
Неравенства Муна не нужны в нашем подходе. Наше новое условие
устойчивости является очень простым и используется, чтобы мы могли
решать неравенства, необходимые для обеспечения статической и
динамической обратной связи по выходу для стабилизации таких систем.
, не требуя необходимости преобразования какой-либо модели системы.
Начальный критерий находится на основе неравенства, включающего
различные матриц, которые могут быть свободно выбраны, и улучшенный
критерий затем находится тщательно выбирая эти матрицы с учетом
корреляции между состояниями системы при различных задержках.
Неравенства Муна не нужны в нашем подходе. Наше новое условие
устойчивости является очень простым и используется, чтобы мы могли
решать неравенства, необходимые для обеспечения статической и
динамической обратной связи по выходу для стабилизации таких систем.
Рассмотрим следующую дискретную систему с нестационарной задержкой по
состоянию (1):
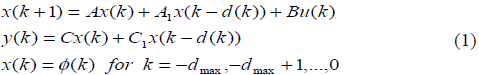
где
k - это дискретное время, 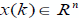 вектор состояния,
вектор состояния, 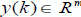 - измеряемые переменные и
- измеряемые переменные и 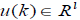 - управляемый вход систеы, A, A1, C и C1 - матрицы системы с
соответствующими измерениями.
- управляемый вход систеы, A, A1, C и C1 - матрицы системы с
соответствующими измерениями. 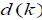 ,
упоминающийся как в уравнениях динамических и статических измерений,
является задержкой состояния, как это часто наблюдается в различных
инженерных системах.
,
упоминающийся как в уравнениях динамических и статических измерений,
является задержкой состояния, как это часто наблюдается в различных
инженерных системах. 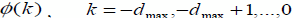 - заданная последовательность начальных условий. Естественное
предположение по
- заданная последовательность начальных условий. Естественное
предположение по 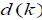 может быть сделано:
может быть сделано:
Предположение 1.
Время задержки 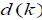 предполагается, что меняется со временем в некоторых пределах,
удовлетворяющих
предполагается, что меняется со временем в некоторых пределах,
удовлетворяющих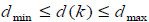 ,
где
,
где 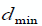 и
и
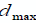 -
положительные константы представляют минимальные и максимальные
задержки, соответственно.
-
положительные константы представляют минимальные и максимальные
задержки, соответственно.
Изменяющаяся во времени задержка 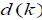 сводится к постоянной задержке
сводится к постоянной задержке  , когда
, когда  .
.
В данной статье предполагается, что
переменные состояния не в полной мере измеримы, то есть, мы знаем
только частичную информацию о  ,
например, некоторые компоненты
,
например, некоторые компоненты  , и что мы заинтересованы в создании регулятора обратной связи по
выходу, такого, что полученная замкнутая система является
асимптотически устойчивой. Для того, чтобы проанализировать
эффективность дискретных систем с запаздыванием, введем следующие
определения устойчивости и асимптотической устойчивости для дискретных
систем [1].
, и что мы заинтересованы в создании регулятора обратной связи по
выходу, такого, что полученная замкнутая система является
асимптотически устойчивой. Для того, чтобы проанализировать
эффективность дискретных систем с запаздыванием, введем следующие
определения устойчивости и асимптотической устойчивости для дискретных
систем [1].
Определение 1:
Дискретная система с задержкой, приведенная в (1), когда  , считается устойчивой, если для любого
, считается устойчивой, если для любого 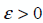 , есть такое
, есть такое  , что
, что 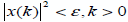 , при
, при 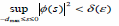 .
.
В дополнение, если  при любых начальных условиях, то система заданная в (1) при
при любых начальных условиях, то система заданная в (1) при  считается асимптотически устойчивой.
считается асимптотически устойчивой.
Предположение 2: Мы
предполагаем, что матрицы А и А1 в системе приведенной в (1) имеют
следующий вид:
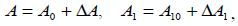
где
 - известные постоянные матрицы соответствующих размеров, а
- известные постоянные матрицы соответствующих размеров, а  и
и 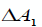 - вещественные нестационарные матричные функции, представляющие
ограниченная по норме допустимых неопределенностей.
- вещественные нестационарные матричные функции, представляющие
ограниченная по норме допустимых неопределенностей.
Определение 2. Система с
неопределенной временной задержкой приведенная в (1) в предположении 2
считается робастно устойчивой, если тривиальное решение 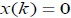 функционального дифференциального уравнения связанное с системой
приведенной в (1) с
функционального дифференциального уравнения связанное с системой
приведенной в (1) с 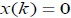 - глобально равномерно асимптотически устойчиво для всех допустимых
неопределенностей [2].
- глобально равномерно асимптотически устойчиво для всех допустимых
неопределенностей [2].
 байт/сек. между
байт/сек. между 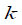 и
и  узлами (рисунок 1). Если линия связи между узлами
узлами (рисунок 1). Если линия связи между узлами 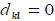 .
.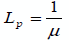 байт.
Также для простоты будем полагать, что поток данных, возникающий в узле
байт.
Также для простоты будем полагать, что поток данных, возникающий в узле
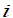 и
предназначенный узлу
и
предназначенный узлу 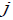 , является простейшим со средней интенсивностью
, является простейшим со средней интенсивностью 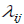 пакетов/сек. Соответственно, полная средняя интенсивность трафика в
сети определяется по формуле
пакетов/сек. Соответственно, полная средняя интенсивность трафика в
сети определяется по формуле 
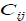 узлу
узлу 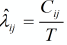 .
.

 -
доля потока
-
доля потока  . Величины
. Величины  в
игровом методе построения ПРИ и выбора маршрутов. Основное их отличие
заключается в том, что они являются характеристикой потока строго
заданного маршрута между узлами
в
игровом методе построения ПРИ и выбора маршрутов. Основное их отличие
заключается в том, что они являются характеристикой потока строго
заданного маршрута между узлами 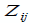 доставки пакетов между узлами
доставки пакетов между узлами 
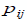 - вероятность передачи сообщения от узла
- вероятность передачи сообщения от узла 


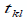 - среднее время пребывания сообщений в линии.
- среднее время пребывания сообщений в линии.
 - среднее время передачи пакета по каналу
- среднее время передачи пакета по каналу 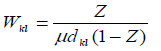 -
среднее время пребывания пакета в буфере. Величина нагрузки в данном
случае определяется как
-
среднее время пребывания пакета в буфере. Величина нагрузки в данном
случае определяется как 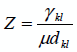 .
Таким образом, получаем следующее выражение для среднего времени
пребывания пакета в системе:
.
Таким образом, получаем следующее выражение для среднего времени
пребывания пакета в системе:

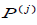 , используемые в игровом методе при формировании маршрутов движения
заявок. К сожалению, на сегодняшний день отсутствует общее решение
данной задачи, но известны ее частные решения [4].
, используемые в игровом методе при формировании маршрутов движения
заявок. К сожалению, на сегодняшний день отсутствует общее решение
данной задачи, но известны ее частные решения [4].