ЗАДЕРЖКИ
Авторы: Борейко О.В. , Никитенко Д.Г., Казакова Е.И..
Источник: Математична культура інженера. Матеріали студентської науково-технічної конференції, 10 квітня 2012р., м. Донецьк: ДонНТУ — с. 96-99.
Традиционной при проектировании цифровых систем управления является
гипотеза про то, что период дискретности является постоянным, и он не
меняется во время эксплуатации системы. Но современная технология
реализации систем автоматики базируется на использовании развитых
телекомуникационных сетей, таких как DeviceNet, Ethernet, FireWire и
других, которые связывают датчики и исполнительные механизмы с
контроллерами, то есть между контроллером (управляющая часть системы) и
объектом с датчиками и исполнительными механизмами находится
телекомуникационная сеть, ресурсы которой используют также другие
контроллеры. В таких сетях могут возникать коллизии, которые приводять
к тому, что контроллер получает необходимую информацию про состояние
объекта не в дискретные равноотдаленные моменты времени, а со случайным
сдвигом во времени относительно того периода дискретности, который был
приемлимым во время проектирования системы. Неопределенность сети с
пакетной передачей информации, где пакеты могут быть потеряны или
испорчены, также ведет к увеличению промежутка времени между отсчетами.
Второй причиной, которая может быть расценена как случайная смена
периода дискретности, является задержка датчиком изготовления нужной
контроллеру информации, потому что эта информация возникает вледствие
сложных расчетов, которые могут длиться некоторое время. Увеличение
периода дискретности негативно влияет на качество системы управления и
может быть причиной потери её устойчивости. Именно эта проблема в
последние годы все больше привлекает внимание исследователей, которые
работают в области систем управления.
В последние годы появилась возможность
провести исследование устойчивости
сетевых систем автоматического управления
при случайной смене периода дискретности
на основании теории робастных систем.
Период дискретизации рассматривается
как параметр, изменение которого ведет
к параметрической неопределенности
передаточной функции цифрового регулятора
(аддитивной или мультипликативной).
Если рассмотреть условия робастной
устойчивости системы, то может быть
получена оценка максимального изменения
периода дискретности, при котором
система остается устойчивой.
Рассмотрим следующую дискретную систему с нестационарной задержкой по
состоянию (1):
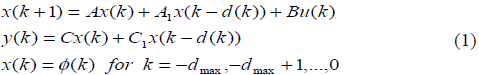
где
k - это дискретное время, 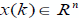 вектор состояния,
вектор состояния, 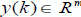 - измеряемые переменные и
- измеряемые переменные и 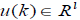 - управляемый вход систеы, A, A1, C и C1 - матрицы системы с
соответствующими измерениями.
- управляемый вход систеы, A, A1, C и C1 - матрицы системы с
соответствующими измерениями. 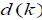 ,
упоминающийся как в уравнениях динамических и статических измерений,
является задержкой состояния, как это часто наблюдается в различных
инженерных системах.
,
упоминающийся как в уравнениях динамических и статических измерений,
является задержкой состояния, как это часто наблюдается в различных
инженерных системах. 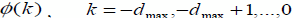 - заданная последовательность начальных условий. Естественное
предположение по
- заданная последовательность начальных условий. Естественное
предположение по 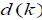 может быть сделано:
может быть сделано:
Предположение 1.
Время задержки 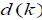 предполагается, что меняется со временем в некоторых пределах,
удовлетворяющих
предполагается, что меняется со временем в некоторых пределах,
удовлетворяющих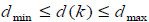 ,
где
,
где 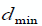 и
и
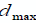 -
положительные константы представляют минимальные и максимальные
задержки, соответственно.
-
положительные константы представляют минимальные и максимальные
задержки, соответственно.
Изменяющаяся во времени задержка 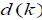 сводится к постоянной задержке
сводится к постоянной задержке  , когда
, когда  .
.
В данной статье предполагается, что
переменные состояния не в полной мере измеримы, то есть, мы знаем
только частичную информацию о  ,
например, некоторые компоненты
,
например, некоторые компоненты  , и что мы заинтересованы в создании регулятора обратной связи по
выходу, такого, что полученная замкнутая система является
асимптотически устойчивой. Для того, чтобы проанализировать
эффективность дискретных систем с запаздыванием, введем следующие
определения устойчивости и асимптотической устойчивости для дискретных
систем [1].
, и что мы заинтересованы в создании регулятора обратной связи по
выходу, такого, что полученная замкнутая система является
асимптотически устойчивой. Для того, чтобы проанализировать
эффективность дискретных систем с запаздыванием, введем следующие
определения устойчивости и асимптотической устойчивости для дискретных
систем [1].
Определение 1:
Дискретная система с задержкой, приведенная в (1), когда  , считается устойчивой, если для любого
, считается устойчивой, если для любого 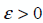 , есть такое
, есть такое  , что
, что 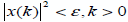 , при
, при 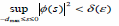 .
.
В дополнение, если  при любых начальных условиях, то система заданная в (1) при
при любых начальных условиях, то система заданная в (1) при  считается асимптотически устойчивой.
считается асимптотически устойчивой.
Предположение 2: Мы
предполагаем, что матрицы А и А1 в системе приведенной в (1) имеют
следующий вид:
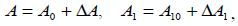
где
 - известные постоянные матрицы соответствующих размеров, а
- известные постоянные матрицы соответствующих размеров, а  и
и 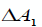 - вещественные нестационарные матричные функции, представляющие
ограниченная по норме допустимых неопределенностей.
- вещественные нестационарные матричные функции, представляющие
ограниченная по норме допустимых неопределенностей.
Определение 2. Система с
неопределенной временной задержкой приведенная в (1) в предположении 2
считается робастно устойчивой, если тривиальное решение 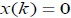 функционального дифференциального уравнения связанное с системой
приведенной в (1) с
функционального дифференциального уравнения связанное с системой
приведенной в (1) с 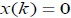 - глобально равномерно асимптотически устойчиво для всех допустимых
неопределенностей [2].
- глобально равномерно асимптотически устойчиво для всех допустимых
неопределенностей [2].