A PROBABILISTIC APPROACH TO THE STABILITY ANALYSIS OF REAL-TIME CONTROL SYSTEMS

Авторы: Manel Velasco, Pau Marti, Rikard Milla, Josep M. Fuertes, Jordi Ayza, Miquel Monroig.

Источник: Department of Automatic Control and Computer Engineering Technical University of Catalonia Pau Gargallo 5, 08028 Barcelona, Spain, {manel.velasco, pau.marti, ricard.villa, josep.m.fuertes, jordi.ayza}@upc.edu.

    Abstract: In real-time multitasking systems, feasible periodic tasks execute within their periods. However, the exact time at which each task executes vary due to other task interferences. For control tasks, this produces irregular sampling and varying time delays, which may degrade system performance and bring the system to instability. In this paper we present stability conditions that allow us to evaluate if a closed-loop system designed to work at a nominal sampling period with a nominal time delay will remain stable if the run-time sampling is not strictly periodic and time delays vary randomly. In the closed-loop system model, we consider the irregular sampling and the varying time delays as random variables with known expectation. With this model, the system evolution can be seen as a sequence of random state vectors generated by the system closed-loop matrix. Then, we derive stability conditions for the system in terms of convergence of a sequence of random variables.
Copyright 2005 IFAC.

   Keywords: Real-time systems, Timing jitter, Random variables, Probabilistic models, Stability tests.

        1. INTRODUCTION
    In real-time multitasking systems, feasible periodic tasks execute within their periods. However, the exact time at which each job executes vary due to other task interferences. That is, real-time systems allow jitter in task executions as far as feasibility constraints are met. In such systems, controllers are often implemented as periodic tasks, where at each job execution, sampling, control algorithm computation and actuation are sequentially performed. In this context, variability in jobs execution produces sampling and latency jitter (Arzen et al., 2000), which may degrade control system performance and even bring the system to instability (Marti et al., 2001b).
    Recently, several works combining control and scheduling co-design approaches have focused on the jitter problem (e.g., (Cervin, 1999) and (Marti et al., 2001a)). Their main goal has been to minimize the degrading effects that jitter in control tasks introduces in the performance of control systems. This is achieved by computing and switching controllers according to the run-time jitters. In addition, several tools have been presented for simulation and performance analysis of real-time control systems (e.g. (Henriksson et al., 2002) and (Lincoln and Cervin, 2002)). However, none of the previousworks focused on control systems stability (although stability issues were considered).
    Looking at stability and the jitter problem for control tasks, in (Marti et al., 2001c), a sufficient stability condition was presented for analysing closed-loop systems where control tasks subject to jitter adapt their gains at run time (i.e., switching controllers). Necessary and sufficient stability conditions that can be also applied in these scenarios can be found in (Dogruel and Ozguner, 1995) or (Liberzon et al., 1999). However, the application of these conditions requires previous knowledge of the exact jitter values that each control task will be subject to at run time. And for some application scenarios, this may not be known previously or could be impossible to predict due to the dynamics of the real-time multitasking system. In these cases, the application of these stability criteria fails and new criteria are required.
    The application of the stability criteria we present does not require knowing the exact jitter values, but their distribution. Our approach is based on modelling the irregular sampling and varying time delay as random variables with known expectation. With this model, the evolution of the system can be seen as a sequence of random state vectors generated by the system closed-loop matrix. Then, we derive stability conditions in terms of convergence of a sequence of random variables. Results are illustrated using simulated examples.
    In addition, the stability criteria we present do not assume switching controllers at run-time. We let the system run a single discrete-time controller designed assuming a constant sampling period and a constant (or zero) time delay . The stability tests we present can be used to analyse whether the closed-loop system will remain stable if the run-time sampling is not strictly periodic and time delays are not constant.

    2. THE JITTER PROBLEM
    In this section we briefly review the jitter problem that may arise in real-time multitasking systems, which may result in random sampling and varying time delays for control systems.
    In real-time scheduling, controllers are usually implemented using the periodic task model. A periodic task is seen as a successive execution of jobs. The kth job of a feasible periodic task fulfils the following constraints: it has to execute within its period, which starts at k1t and finishes at (where T is the task period), and has to complete before or at time k1t +D, where D is its relative deadline (provided , where C is the task worst-case execution time). This means that each job will start and finish its execution within an interval of D time units (usually D = T), but no assurances can be made on the exact start and completion time of each job execution because of the interference of other tasks executions.

    A common way of coding classically designed controllers using the periodic task model is to set each control task period T equal to the sampling period 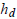used in the controller design stage (with D=T). Sampling and actuation are assumed to take place when each job starts and completes its execution respectively. With this assumption, the allowed variability in jobs executions results in random sampling and varying time delays. This is problematic because control actions are calculated with respect to the assumptions on regular sampling and constant time delay that were made in the controller design stage.
    Example 1 illustrates the jitter phenomena of real-time multitasking systems and its influence on the control signal for a generic controller.
   Example 1. Let us consider a real-time multitasking system with three control tasks, as specified in Table 1 (where periods P, deadlines D and worst-case computation times C are given in seconds).

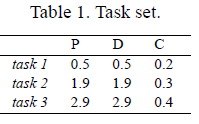
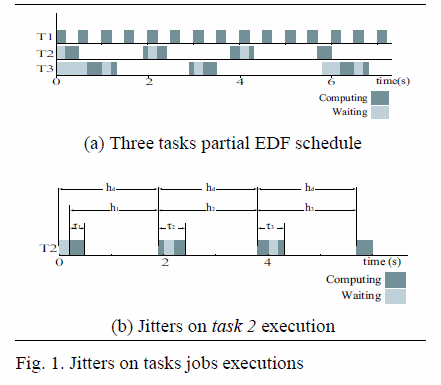
Figure 1 (a) shows a partial feasible schedule of the three tasks (during 7s, approximately) if the task set is scheduled using the optimal priority-based scheduling algorithm earliest deadline first (EDF) (Liu and Layland, 1973). For each task, dark grey symbolizes jobs executions, which may be blocked (symbolized in light grey) due to the interference of other tasks executions. These interferences, which are allowed as far as schedulability constraints are satisfied, cause jitter in jobs execution.

    Looking for example at the sequence of jobs of task 2 (Figure 1 (b)), we have that the time interval between consecutive jobs start execution times, i.e., sampling period, takes different values. And the time elapsed from each job start execution time to its completion time, i.e., latency or delay, also varies. In fact, the task was assigned a period of hd = 1:9s (because this value was used in the controller design stage), but at run-time, the real sampling period varies in the vicinity of 1:9s, taking values at 1:7s, 1:9s and 2s. In addition, in the controller design a delay of 0:3s was accounted for, but at run-time, the real latency varies, taking values of 0:3s but also of 0:5s.
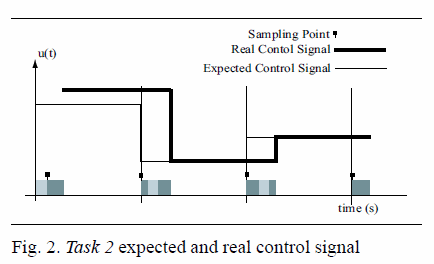
    Figure 2 shows the evolution of the control signal for each job execution. In fact, it shows the evolution of the expected control signal (thin line, corresponding to a classically designed controller executing in isolation, that is, without jitters) and the real control signal (thick line) for the same controller if implemented in task 2 in the multitasking real-time system . In Figure 2, let us suppose for example that a perturbation affects the system controlled by task 2 just before time 0. The first sampling that would detect that the controlled system is not in equilibrium (due to the perturbation) should occur at time 0. But due to a start time delay, sampling occurs 0:2s later. Therefore, the sampling will read a greater value (corresponding to a greater deviation of the controlled system with respect to its equilibrium point) than it should. Consequently the real control signal will be stronger (higher valued) than the expected one, because it will try to correct a greater deviation. Therefore, the evolution of the controlled system will not be the expected one. We don’t know if the system will remain stable as it would do if the controller would execute in isolation, without suffering jitters.
    By treating these jitters as random variables, this paper presents a new (to the authors knowledge) probabilistic approach to the stability analysis of control systems subject to sampling and latency jitter.

    3. PROBLEM FORMULATION
    In this section we present the system model we use to derive the stability criteria.We then define the problem to be analysed for the stability analysis, and without losing generality, we reduce the system model that we consider in order to simplify notation.
    3.1 System model
    A linear discrete-time control system with time delay (where the delay is less than or equal to the sampling period) can be described by equation (1), where xn is the state vector, 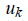and uk1 are the current and past control signals, andare the system and input matrices that depend on the sampling period h and time delay t (Astrom and Wittenmark, 1997).

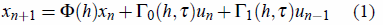
Consider that the sampling period h and time delay t are independent random variables with known expectation but the control signal u is given by a controller designed to work at a constant sampling period 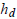with a constant time delay . The new closed-loop system dynamics can be described by (2),

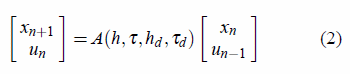
where is the closed-loop matrix next specified in (3). In (3), 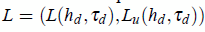is the feedback gain.

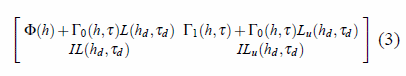
To clarify the notation, the closed-loop matrix (3) can be further detailed as in (4).

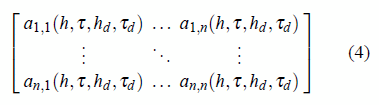
    3.2 Problem definition
    The closed-loop system given by (2) may become instable because control signals are not appropriate according to the system dynamics. Control signals u are computed according to the feedback gain L, that was designed assuming a constant sampling period 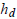and a constant time delay . However, the run-time system evolution is discretely driven by random variables h and t , which take unexpected but bounded values at each iteration.
    To focus on the stability of the closed-loop system given by (2), we analyse the convergence of the sequence of state vectors that it generates. To do so we use known concepts of convergence of sequences of random variables (Grimmett and Stirzaker, 2001). Note that looking at (2) we have to study which conditions the generated sequence of random state vectors x1; :::;xn has to fulfil in order to converge towards a random vector x = 0.
    Henceforth, convergence will refer to convergence in mean (recall that convergence in mean implies convergence in probability (Grimmett and Stirzaker, 2001)). We say that the sequence Xn converges in mean towards X, if , and:

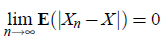
where the operator E denotes the expectation. Therefore, to establish stability conditions for the closed-loop system given by (2), we will focus on studying the convergence in mean of the sequence of state vectors xn towards x. That is,

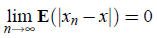
In fact, if the equilibrium point is zero (without losing generality), then, we study

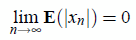
In order to establish convergence criteria, we shall look at the sequence given by E(jxnj). If such sequence converges towards zero, then, the sequence of state vectors will converge in mean. Therefore, the closed loop system specified in (2) will be stable.

    4. CONCLUSIONS
    We have discussed why in the application scenario of real-time control systems (where controllers are subject to scheduling induced jitters), existing stability criteria may not be applicable. To overcome this applicability problem, in the closed-loop system designed to work with regular sampling and assuming a constant time delay, we have modeled the jitter effects on the sampling and controller latency as bounded random variables. Then, we have derived stability conditions in terms of convergence of the random state vectors generated by this new model. Using this stability test has the advantage of obtaining a closer result to real situations.
    Future work will focus on using the stability conditions for the design of more flexible and adaptive schedulers.

    REFERENCES
  1. Arzen, Karl-Erik, Anton Cervin, Johan Eker and Lui Sha (2000). An introduction to control and scheduling co-design. In: Proceedings of the 39th IEEE Conference of Decision and Control. Sydney, Australia.
  2. Astrom, Karl J. and Bjorn Wittenmark (1997). Computer-Controlled Systems. Third Edition. Prentice–Hall.
  3. Cervin, Anton (1999). Improved scheduling of control tasks. In: Proceedings of the 11th Euromicro Conference on Real-Time Systems. York, UK.
  4. Dogruel, M. and U. O¨ zgu¨ner (1995). Stability of a set of matrices: A control theoretic approach. In: Proceedings of the 34th IEEE Conference of Decision and Control.
  5. Grimmett, Geoffrey and David Stirzaker (2001). Probability and Random Processes. Third Edition. Oxford University Press.
  6. Henriksson, Dan, Anton Cervin and Karl-Erik Arzen (2002). Truetime: Simulation of control loops under shared computer resources. In: 15th IFAC World Congress on Automatic Control. Barcelona, Spain.
  7. Lancaster, Peter and Miron Tismenetsky (1985). The Theory of Matrices. Second edition. Academic Press.
  8. Liberzon, D., J.P. Hespanha and A.S. Morse (1999). Stability of switched systems: a lie-algebraic condition. Systems Control Letters 37, 117–122.
  9. Lincoln, Bo and Anton Cervin (2002). Jitterbug: A tool for analysis of real-time control performance. In: 41st IEEE Conference on Decision and Control. Las Vegas, NV.
  10. Liu, C. L. and James W. Layland (1973). Scheduling algorithms for multiprogramming in a hard-realtime environment. Journal of the Association for Computing Machinery 20(1), 46–61.
  11. Marti, Pau, Josep M. Fuertes, Gerhard Fohler and Krithi Ramamritham (2001a). Jitter compensation for real-time control systems. In: Proceedings of the 22nd IEEE Real-Time Systems Symposium (RTSS 2001). London, Uk.
  12. Marti, Pau, Ricard Vill`a, Josep M. Fuertes and Gerhard Fohler (2001b). On real-time control tasks schedulability. In: European Control Conference. Porto, Portugal.
  13. Marti, Pau, Ricard Vill`a, Josep M. Fuertes and Gerhard Fohler (2001c). Stability of on-line compensated real-time scheduled control tasks. In: IFAC Conference on New Technologies for Computer Control. Hong Kong, China.