Реферат по теме выпускной работы
Содержание
- Введение
- 1. Цель и задачи исследования, планируемые результаты
- 2. Актуальность темы
- 3. Общие сведения о графах
- 4. Обзор существующих алгоритмов для поиска кратчайших путей в графе
- 5 Метод построения кратчайших путей в двухуровневом графе
- Выводы
- Список источников
Введение
Часто
бывает
полезно и
наглядно изображать некоторую ситуацию в виде рисунка, который состоит
из точек
(вершин), изображающие основные элементы ситуации, и линий (ребер),
которые
соединяют определенные пары этих вершин и изображают связи между ними. Такие
рисунки
известны под общим названием –
графы. Графы
встречаются во многих областях под разными названиями:
«структуры» в
гражданском строительстве, «сеть» в электротехнике,
«социограммы» в социологии
и экономике, «молекулярные структуры» в химии,
«дорожные карты» и другие [15].
Бурное
развитие
вычислительной техники позволяет решать все более сложные теоретические
и
прикладные задачи, в свою очередь требует совершенствования методов их
решения.
Широкое
распространение технологии параллельных и распределенных вычислений
позволяет
по-новому взглянуть на решение многих задач, а также на методы и
алгоритмы,
раньше казались бесперспективными из-за высокой вычислительной
сложности. В
задачи высокой вычислительной сложности относятся частности задачи
оптимизации.
Одной
из таких задач является задача поиска кратчайшего пути на графе. Задача
имеет много практических применений, в их число можно отнести поиск
кратчайшего
пути между городами, поиск пути передачи информации, который
обеспечивает
минимальную стоимость и минимальное количество времени передачи или
максимальную надежность при распространении информации в разветвленной
сети.
Целью
магистерской работы является разработка метода поиска кратчайших
путей в помеченном
двухуровневом графе и программная реализация разработанного метода.
1. Цель и задачи исследования, планируемые результаты
Объектом исследования в работе является двухуровневый граф с N вершинами. Каждая вершина графа первого уровня выступает графом второго уровня с M вершинами.
Предметом исследования является метод поиска кратчайших путей в помеченном двухуровневом графе.
Основной задачей является разработка и программная реализация метода поиска кратчайшего пути между начальной и любой из финальных вершинами двухуровневого графа и расчет качества (стоимости) этого пути.
Входными данными для метода является помеченный двухуровневый граф, выходными данными является пометка кратчайшего пути между заданными вершинами, а также качество этого пути.
2. Актуальность темы
Проблема поиска кратчайших путей в графе является общеизвестной и важной для различных приложений. Существует ряд алгоритмов для решения этой задачи. В последнее время эта проблема интенсивно изучается для графов сложной многоуровневой структуры. В данной работе рассматривается задача поиска кратчайших путей в помеченном двухуровневом графе от начальной вершины до некоторой финальной.
Актуальность проблемы для таких сложных графов заключается в том, что в прикладных задачах кратчайшие пути нужно находить для перевозок, проходящих через пути, города, сложные транспортные развязки. Поэтому тематика данной работы достаточно актуальна.
3. Общие сведения о графах
Граф – это совокупность объектов со связями между ними. Объекты рассматриваются как вершины, или узлы графа, а связи – как дуги, или ребра.
Для различных областей использования виды графов могут отличаться ориентируемостью, ограничениями на количество связей и дополнительными данными о вершинах или ребра. Большое количество структур, которые имеют практическую ценность в математике и информатике, могут быть представлены графами.
Граф G – это упорядоченная пара G = (V; E), для которой выполняются следующие условия: V – множество вершин или узлов E – множество пар (в случае неориентированного графа – неупорядоченных) вершин, которые называют ребрами V и E обычно считаются конечными множествами.
Основные элементы графа состоят из вершин графа, ребер графа и дуг графа. Сочетание этих элементов определяет понятия: неориентированный граф, ориентированный граф и смешанный граф.
Неориентированный граф – это граф (рисунок 3.1), для каждого ребра которого несуществен порядок двух его конечных вершин.
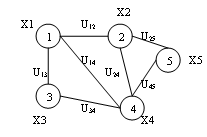
Ориентированный граф – это граф, для каждого ребра которого существенен порядок двух его конечных вершин (рисунок 3.2).
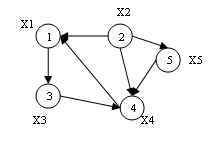
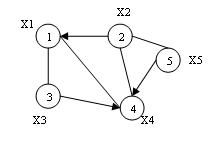
Смешанный граф (рисунок 3.3) – это граф, содержащий как ориентированные, так и неориентированных ребра. Любой из перечисленных видов графа может содержать одно или несколько ребер, у которых оба конца сходятся в одной вершине, такие ребра называются петлями (рисунок 3.4).
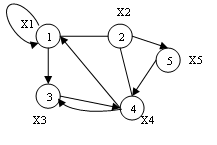
Рисунок
3.4 –
Пример
смешанного графа с петлями
Если пара вершин соединяется несколькими ребрами или дугами одного направления, то ребра (дуги) называют кратными (параллельными). Дуга или ребро соединяющий вершину саму с собой называется петлей. Граф без кратных дуг и петель называется простым.
Степень вершины – количество ребер графа G, инцидентных вершине x.
Вес ребра – значение, поставлены в соответствие данному ребру взвешенного графа. Обычно вес – действительное число, в таком случае его можно интерпретировать как «длину» ребра.
Граф, в котором каждому ребру (каждой дуге) поставлено в соответствие определенное неотрицательное число, которое называют весом или длиной ребра (дуги), называют взвешенным графом.
Путем в графе называют конечную последовательность вершин, в которой каждая вершина соединена ребром с последующей в последовательности вершин.
Дуги, имеющие общие конечные вершины, называются смежными.
Путь (или цикл) называют простым, если ребра в нем не повторяются; элементарным, если он простой и вершины в нем не повторяются. Ориентированным путем в орграф называют конечную последовательность вершин V i, для которой все пары (Vi, V i + 1) есть (ориентированными) ребрами.
Длиной пути (машрут) во взвешенном графе называют сумму длин звеньев этого пути (машрут).
Количество
k
ребер в пути называется длиной пути. Говорят,
что этот путь соединяет вершины v1
и vk
+1
или ведет с вершины v1 в
вершину vk
+1.Путем
длины 0
считается последовательность, состоящая из
единственной вершины.
Путь, в
котором все ребра попарно различны, называется цепью. Путь,
в котором все промежуточные вершины попарно различны, называется
простой цепью.
Путь
называют циклом, если в нем первая и последняя вершины совпадают.
4. Обзор существующих алгоритмов для поиска кратчайшего пути в графе
Проблема поиска оптимальных решений является базовой в различных областях науки и техники и требует разработки средств эффективного решения. Часто оптимизационные задачи можно свести к формализованного вида и взаимосвязь составных частей математической модели представить в виде графа. Такой подход позволяет использовать алгоритмы и средства теории графов в процессе поиска оптимальных решений и минимизации аналитических моделей критериев оптимальности. Решение задачи тогда сводится к поиску кратчайших путей между вершинами графа.
Широкий круг оптимизационных задача сводится к описанию математической модели системы с помощью средств теории графов с определением физического смысла массива вершин и дуг, которые соединяют. Оптимальное решение тогда может быть найдено по определенному алгоритму теории графов с помощью автоматизированной системы поиска оптимальных решений:
– для поиска кратчайшего пути между двумя вершинами графа используется алгоритм Дейкстры, который требует меньше временных затрат по сравнению с подобными алгоритмами;
– поиск кратчайших путей между всеми вершинами графа осуществляется с помощью алгоритма Флойда;
– найти минимальный путь в графе с ребрами единичной длины позволяет волновой алгоритм.
5. Метод построения кратчайших путей в двухуровневом графе
Рассматриваются неорграфы с конечным множеством вершин Q и ребер E, не имеющие петель. Ребро – это пара вершин (q, u). Ребра графа G отмечено метками из множества Y, выделено начальную вершину и множество финальных вершин. Таким образом, G = (Q, E, Y, ρ, q0, F), где
Q – конечное множество вершин графа G;
E – множество ребер графа G;
Y – множество пометок ребер графа G;
ρ:
E → Y –
функция разметки ребер графа G;
q0 – начальная вершина графа G;
F – множество финальных вершин графа G.
Граф G будем называть графом первого уровня. Каждая Q графа G является графом Gi – графом второго уровня без петель и кратных дуг, в котором вершины и ребра отмечено метками из множеств M и P соответственно. Так, Gi = (Ti, Di, Mi, Pi, μ, t, n0, fi), где:
Ti – конечное множество вершин графа Gi;
Di – множество дуг графа Gi;
Mi – множество пометок вершин графа Gi;
Pi – множество пометок дуг графа Gi;
μ: T → M – функция разметки вершин графа Gi;
t: D → P – функция разметки дуг графа Gi;
n0 – начальная вершина графа Gi;
fi – финальная вершина графа Gi.
Вершина графа Gi имеет следующий вид: (qi; tj), где qi – номер вершины графа G, а tj – номер вершины графа Gi. Дуга графа G объединяет уникальную пару вершин различных графов Gi.
Каждой вершине qi графа G поставим в соответствие число Z (qi) – качество этой вершины.
Путем
в графе G назовем конечную
последовательность l
= q1 e1 q2 e2…ek-1
qk, где ei – дуга,
началом которой есть вершина qi, а концом – qi+1
Путем в графе Gi назовем конечную последовательность s = (q1; ti) d1 (q2; tj) d2 ... dk-1, где di – дуга, началом которой является вершина (qi; tj).
Отметка пути s – это последовательность отметок w (s) = m1 p1 m2 p2 ... pk-1 mk, где mi = μ (Ti), pi = t (di).
Генеральным путем назовем последовательность I = (q1; ti) x1 (q2; tj) x2 ...(qk; tn) xk-1, где (qk; tn) принадлежит Ti, а xi может быть дугой ei графа G или дугой di графа Gi .
Отметка пути I – это последовательность отметок w (I) = a1 b1 a2 b2 ... bk-1 ak, где ai = μ (Ti), bi = ρ (ei) или bi = t (di).
Весом
генерального пути I между
вершинами qi и qj, будем называть вес пути
между
вершинами (qi; tn) и (qj; tm) и определим ее величину по
формуле на рисунке 5.1.
Качество генерального пути I определим через величину dis (I) по формуле на рисунке 5.2.
Рисунок 5.2 – Формула качества генерального пути
Для вершины qi определим множество Pre (qi) = (qj | (qj, qi) = ei) и множество Post (qi) = (qj | (qi, qj) = ei).
Метод построения кратчайших путей в двухуровневом графе.
Входные данные: замечен двухуровневый граф G с начальным и множеством финальных вершин.
Выходные данные: одна или несколько пометок кратчайших путей, качество этих путей.
Шаг 1.
1.1) Для неориентированных графов G для каждого ребра между парой вершин qi и qj вводится две дуги: (qi, qj) и (qj, qi).
1.2) В список вершин графа G вводится фиктивная конечная вершина fin, а в список дуг – дуга с каждой финальной вершины qi в вершину fin. Эта дуга обозначается отметкой μ (qi; tj).
1.3) Создаем представление графа G в виде списка дуг с их отметками и весом, при этом отметки соответствующих вершин графов Gi переносятся на дуги графа G (например, если пометками двух вершин и дуги между ними будут соответственно (qi, tn), (qj, tm) и xw, то после переноса пометок вершин на дугу, пометка дуги будет иметь следующий вид: (qi, tn ) xw (qj, tm).
1.4) Для каждого ребра графа Gi между парой вершин (qi; tn) и (qj; tm) вводится две дуги: ((qi; tn) (qj; tm)) и ((qj; tm) ((qi; tn)), при этом отметки вершин переносятся на дуги.
Шаг 2. If в графе G существует хоть одна вершина, не является начальной или финальной, из которой выходит хоть одна дуга в финальную, then go to Шаг 3, else go to Шаг 7.
Шаг 3. Выбираем qi = Pre (fin) q: = qi.
Шаг 4. If q ≠ q0 then удаляем вершину q и все входящие и исходящие из нее дуги. If при этом есть некоторый путь qi ek qe qj, где qi = Pre (q) и qj = Post (q), then в граф добавляется дуга (qi, qj) с отметкой ek полученной с помощью операции соединения пометок. Else, если q = q0 go to Шаг 2.
Шаг 5. Удаляем те петли, в пометки которых начало и конец совпадают.
Шаг 6. Замена оператора соединения
На
пунктах 4 –
6
происходит удаление одной вершины.
Для
вершин, пометки которых соеденены оператором соединения (наприклад, (qi; tn) W (qi;
tm)) работает алгоритм [5],
который ищет оптимальний
путь
между этими
вершинами (например, между tn
і tm, где tn – определим
как начальную вершину, а tm – как финальную).
Для этого создадим представление
соответственного графа Gi ( tn, tm ) в виде списка дуг с их от
метками и весом.
If в результате работи
алгоритма [5] оптимальный путь
найден, then пометкой
этого пути заменяем оператор
«W» вместе с двумя
пометками, которые он
соединяет.
If оптимальних
путей
несколько , then в
список дуг графа G
добавляется такая
же дуга, но, соответственно, с другой пометкой.
Else, если пути не существует, then удаляем дугу (qi, qj).
Шаг 7. Удаляем все вершины, которые не являются начальной или финальной и все входящие и исходящие из них дуги. В результате получаем граф, состоящий всего из двух вершин: начальной и финальной.
Вычисляем качество пути QPath для всех дуг графа G, которые объединяют эти вершины. Выберем наименьшее значение QPath, которое и определяет оптимальный путь в графе. Если наименьших значений QPath несколько, то результатом будет несколько путей с этими значениями.
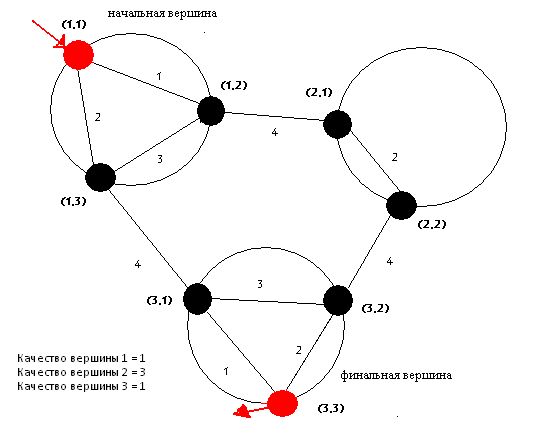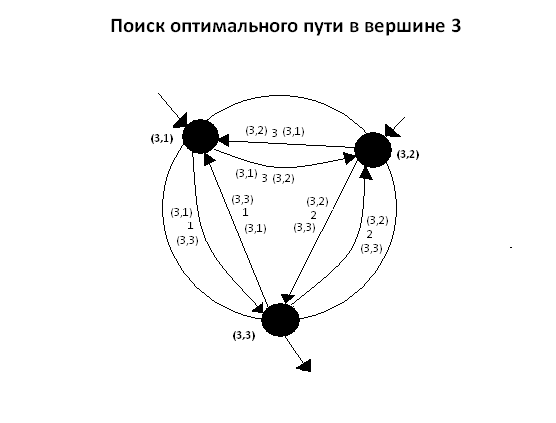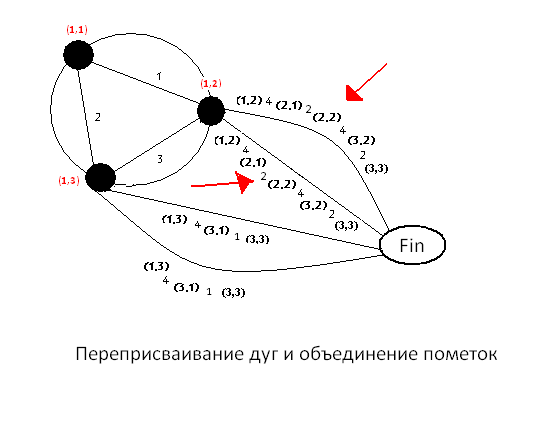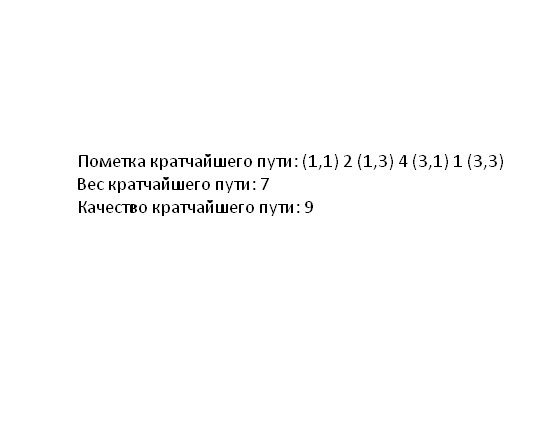
Пример работы метода построения кратчайшего пути в двухуровневом графе представлен на рисунке 5.3.
Рисунок
5.3 – Пример работы метода на двухуровневом графе состоящем
из
трех вершин
(анимация: 25 кадров, 5 циклов повторения, 166 килобайт)
Выводы
Предложен новый метод поиска кратчайших путей в двухуровневом графе с помеченными вершинами и дугами, который работает с двухуровневым графом G без необходимости приводить его к стандартному виду одноуровневого графа, но при этом используется метод локальной редукции графа.
В результате применения метода получаем одну или несколько заметок для оптимальных путей и качество этих путей в графе G.
Легко видеть, что в случае, когда все графы Gi имеют по одной вершине, разработанный метод совпадает с ранее разработанным алгоритмом поиска кратчайшего пути в помеченном графе методом локальной редукции графа [5]. Таким образом, предложенный метод является существенным обобщением ранее разработанного алгоритма. Обобщение заключается в следующем:
1) Каждая вершина графа G является графом Gi.
2) Проводится вычисления качества пути с учетом веса пометки каждой вершины на этом пути и пометки веса каждого ребра в то время, как в [5] выполняется только вычисления веса отметок ребер в пути.
3) Используется алгоритм [5] для графов Gi.
В дальнейшем планируется усовершенствование разработанного метода и его программная реализация
При написании данного реферата
магистерская работа еще не завершена. Окончательное завершение: декабрь
2014 года. Полный текст работы
и материалы по теме могут быть получены у автора или его руководителя
после указанной даты.
Список источников
1. Ногина Н.В. Синтез регулярного выражения языка, порожденного помеченным графом, методом его локальной редукции / Н.В. Ногина, И.С. Грунский // Искусственный интеллект. – 2012. – №3. – с. 348-353.
2. Кристофидес, Н. Теория графов: алгоритмический подход / Н. Кристофидес. – М.: Мир, 1978. – 430 с.
3. Ахо А. Построение и анализ вычислительных алгоритмов / А. Ахо, Дж. Хопкрофт, Дж. Ульман. – М.: Мир, 1979. – 536 с.
4. Батищев Д.И. Многоуровневая
декомпозиция гиперграфовых структур / Батищев Д.И., Старостин Н.В.,
Филимонов
А.В. //
Прилож. к журналу «Информационные технологии»
№5(141).
–
М.: Новые технологии.
–
2008. – 32 с.
5. Ногина
Н.В. Построение
кратчайшего пути в помеченном графе при помощи локальной редукции графа
/ Н.В.
Ногина, А.В. Билык // Сучасна
інформаційна Україна: інформатика, економіка, філософія: матеріали
доповідей конференції, 26 квітня
2012 року. – Донецьк, 2012. – 316 с. – С.
76-79.
6.
Бєлов
В.Теорія графів / Бєлов В.– М. : Питер,1968.
– 304 с.
Полат
Е.С. Новые педагогические и информационные технологии / Полат Е.С.
– М. : Akademia, 1999.
– 401с.
7. Кузнєцов О.П. Дискретная математика для
инженера
/ Кузнєцов О.П.
– М. : Энергоатомиздат,
1988. –
703
с.
8. Оре О. Теорія графів / Оре О. –
М. : Наука,
1980.
– 340 с.
9.
Смольяков
Е.Р. Введение в теоpию гpафов /
Смоляков Е.Р. – М. : МГТУ, 1992. – 705 с.
10. Hечепуpенко
М.И. Алгоpитмы и пpогpаммы pешения
задач на гpафах и
сетях / Hечепуpенко И.М.
– М. : Hаука,
1990. –
202 с.
11. Романовский И.В. Алгоpитмы pешения экстpемальных задач / Романовский И.В. – М. : Hаука, 1977. – 506 с.
12.
Землянухин В.Н. Задачи
оптимизации на графах / В.Н. Землянухин, Л.Н. Землянухина. –
М. : Наука,
2009. – 677 с.
13. Евстигнеев В.А. Графы в
программировании: обработка, визуализация и применение / В.А.
Евстигнеев, В.Н.
Касьянов. – М. :
Наука, 1999.
–
266 с.
14. Новиков Ф.А. Дискретная математика / Новиков Ф.А. – М. : Питер, 2001. – 301 с.
15. Интернет – источник. Алгоритмы на графах
