---

          Построение кратчайшего пути в графе при помощи локальной редукции графа

 Авторы: Н.В. Ногина, А.В. Билык
 Источник: Сучасна інформаційна Україна: інформатика, економіка, філософія / Матерiали VI мiжнародної науково-практичної конференцiї студентiв, аспiрантiв та молодих вчених. – Донецьк, ДонНТУ – 2012, секція 2, с. 76 - 79. [Перейти]

   Аннотация

   Ногина Н.В., Билык А.В. Построение кратчайшего пути в графе при помощи локальной редукции графа. Рассмотрен алгоритм построения кратчайшего пути в помеченном графе при помощи локальной редукции графа

   Общая постановка проблемы

Задача поиска кратчайших путей в графе является широко известной и важной для разнообразных приложений. Известен ряд алгоритмов решения этой задачи. В настоящем докладе рассматривается задача поиска кратчайшего пути в помеченном графе от начальной вершины к некоторой финальной. В отличие от известных алгоритмов, предложен алгоритм решения, основанный на известном методе перехода от отмеченного  графа к регулярному выражению, описывающему все пути из начальной в финальные вершины. Предлагаемый алгоритм является модификацией алгоритма из [3].

Помеченным графом назовем восьмерку G=(Q, E, X, Y, µ, ρ, q₀, F), где Q – конечное множество вершин, E – множество дуг, X – множество отметок вершин, Y – множество отметок дуг, µ: Q→X – функция разметки вершин, ρ: E→Y – функция разметки дуг, q₀ – начальная вершина, F–множество финальных вершин. Предполага­ется, что множества  Q, E, X, Y – конечны, а пометки y – положительные действительные числа.

Путем в графе G будем называть конечную последовательность l = q₁ e₁ q₂ e₂…e_k-1 q_k, где q_i – вершина, e_i – дуга, началом которой является вершина q_i, а концом – q_i+1. Отметка пути l – это последовательность отметок w(l)=x₁ y₁ x₂ y₂…y_k-1 x_k, где x_i = µ(q_i), y_i = ρ(e_i).

Пусть Pre(q_i) – множество начальных вершин всех дуг, входящих в q_i; Post(q_i) – множество конечных вершин всех дуг, исходящих из q_i. Весом пути между вершинами q₀ и q_k назовем  величину на рисунке 1.1.

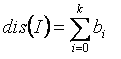
Рисунок 1.1 – Формула веса пути

   Алгоритм

         Дан помеченный граф G с начальной и множеством финальных вершин.

Требуется построить отметку кратчайшего по весу пути.

Шаг 1. Создаем представление графа G в виде списка дуг с их отметками и весом, при этом отметки соответствующих вершин переносятся на дугу. Для неориентированных графов для каждого ребра между парой вершин q_i и q_j вводится две дуги: (q_i,q_j) и (q_j,q_i). В список вершин вводится фиктивная конечная вершина fin, а в список дуг – дуга из каждой финальной вершины q_i в вершину fin. Эта дуга помечается отметкой µ(q_i).

Шаг 2. If   в графе существует хоть одна петля или существуют вершины, не являющиеся начальными, из которых исходит хоть одна дуга,  then go to  Шаг 3

Else go to  Шаг 6.

Шаг 3. Удаление кратных дуг и петель

1. Удаляем все кратные дуги кроме одной из них с минимальным  весом dis.

2. Удаляем все петли, присутствующие в графе.

На шагах 4 – 5 происходит удаление одной вершины.

Шаг 4. Выбираем q_i = Pre(fin);

q:= q_i.

Шаг5. If q ≠ q₀ then удаляем вершину q и все входящие и исходящие из нее дуги. Если при этом есть некоторый путь q_j e_i q e q_k, где q_j = Pre(q) и q_k = Post(q), то в граф добавляется дуга (q_{j ,}q_k) c отметкой, полученной при помощи операции сочленения, описанной в [3];

dis(qj,qk)= dis(qj,q)+ dis(q,qk);  

go to Шаг 2;

else q_i  равная q₀ не исключается;

       выбираем q_m = Pre(q₀);

       q:= q_m  go to Шаг 5.

Шаг 6. Удаляем все вершины, не равные q₀ и fin и все входящие и исходящие из них дуги. Получим граф, состоящий только из двух вершин: начальной и fin, соединенных одной дугой c минимальным весом dis с отметкой кратчайшего пути в графе.

Доказано, что алгоритм корректен.

Данный алгоритм является модификацией алгоритма из [3], определяемой существом задачи. Модификация заключается в следующем.

1. При удалении кратных дуг оставляем дугу с минимальным весом, в то время как в [3] выполняется объединение двух языков.

2. Удаление петель происходит без использования операции зацикливания (итерации), поскольку в кратчайшем пути в графе петли не участвуют.

3. При удалении вершин дополнительно производится вычисление веса dis отметки пути, в то время как в [3] выполняется только конкатенация языков.

4. В результате работы алгоритма вычисляется пометку кратчайшего пути из начальной вершины в одну из финальных, в то время как алгоритм из [3] позволяет находить множество отметок всех путей из начальной вершины  во все финальные.

  Список использованной литературы

1.     Ахо А. Построение и анализ вычислительных алгоритмов / А. Ахо, Дж. Хопкрофт, Дж. Ульман. – М. : Мир, 1979. – 536 с.

2.  Хопкрофт Дж. Введение в теорию автоматов, языков и вычислений. 2-е издание / Дж. Хопкрофт, Р. Мотвани, Дж. Ульман. – М. : Издательский дом "Вильямс", 2002. – 528 с.

3.   Ногина Н.В. Анализ языков, порожденных помеченными графами. / Н.В. Ногина, И.С. Грунский  // Тезисы докладов международной научно-технической конференции «Системный анализ и информационные технологии» (SAIT 2012). – Киев, 2012. – в печати.